Article contents
A note on Taskinen's counterexamples on the problem of topologies of Grothendieck
Published online by Cambridge University Press: 20 January 2009
Extract
By the work of Taskinen (see [4, 5]), we know that there is a Fréchet space E such that Lb(E, l2) is not a (DF)-space. Moreover there is a Fréchet–Montel space F such that 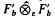 is not (DF). In this second example, the duality theorem of Buchwalter (cf. [2, §45.3]) can be applied to obtain that
is not (DF). In this second example, the duality theorem of Buchwalter (cf. [2, §45.3]) can be applied to obtain that 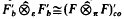 and hence
and hence 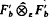 is a (gDF)-space (cf. [1, Ch. 12 or 3, Ch. 8]). The (gDF)-spaces were introduced by several authors to extend the (DF)-spaces of Grothendieck and to provide an adequate frame to consider strict topologies.
is a (gDF)-space (cf. [1, Ch. 12 or 3, Ch. 8]). The (gDF)-spaces were introduced by several authors to extend the (DF)-spaces of Grothendieck and to provide an adequate frame to consider strict topologies.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1989
References
REFERENCES
- 4
- Cited by


