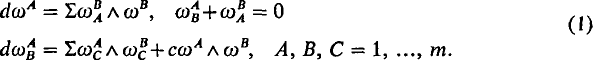Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:29:18.095Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on pseudo-umbilical surfaces

Published online by Cambridge University Press:  20 January 2009

Chorng-Shi Houh
Chorng-Shi Houh
Affiliation:
Wayne State University, Detroit, Mich. 48202
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We follow the notations and basic equations of Chen (2). Let M be a surface immersed in an m-dimensional space form Rm(c) of curvature c = 1, 0 or −1. We choose a local field of orthonormal frames e1, …, em in Rm(c) such that, restricted to M, the vectors e1, e2 are tangent to M. Let ω1, …, ωm be the field of dual frames. Then the structure equations of Rm(c) are given by

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 2 , September 1976 , pp. 137 - 142
Copyright
Copyright © Edinburgh Mathematical Society 1976

References

REFERENCES

(1) Chen, B. Y., Geometry of submanifolds (Marcel-Dekker, New York, 1973).Google Scholar
(2) Chen, B. Y., Pseudo-umbilical surfaces with constant Gauss curvature, Proc. Edinburgh Math. Soc. 18 (1972), 143–148.Google Scholar
(3) Chen, B. Y., Minimal surfaces with constant Gauss curvature, Proc. Amer. Math. Soc. 34 (1972), 504–508.CrossRefGoogle Scholar
(4) Moore, J. D., Isometric immersions of riemannian products. J. Diff. Geometry 5 (1971), 159–168.Google Scholar