No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
Binet shewed that the function
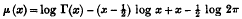
can be expanded as an inverse factorial series. This note furnishes a new and much simpler proof of his result, based on a formula which is an analogue of the Binomial Theorem for factorials.
This formula is that, if we denote by [x]n the ratio
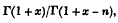
then
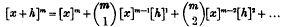
where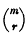 
denotes the coefficient of xr in the expansion of (1 + x)m.
* Journ. de l' Ecole Polyt. 16 (1839), 123.Google Scholar
† The usual proof depends on expressing μ(x) as an integral. See Nielsen, : Handbuch der Theorie der Gammafunktionen; p. 284 et seq.Google Scholar
‡ This is merely the theorem that F(a, b; c; 1) can be expressed as
* Landau, : Munich Sitzungsberichte (1906) 36, 151–221.Google Scholar
You have
Access