Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T01:03:12.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Normal -Fitting classes

Published online by Cambridge University Press:  20 January 2009

J. C. Beidleman  and
M. J. Tomkinson
J. C. Beidleman
Affiliation:
Department of MathematicsUniversity of KentuckyLexington, KY 40506, U.S.A.
M. J. Tomkinson
Affiliation:
Department of MathematicsUniversity of GlasgowGlasgow G12 8QW, U.K.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The authors together with M. J. Karbe [Ill. J. Math. 33 (1989) 333–359] have considered Fitting classes 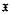of -groups and, under some rather strong restrictions, obtained an existence and conjugacy theorem for 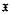-injectors. Results of Menegazzo and Newell show that these restrictions are, in fact, necessary.

The Fitting class 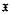is normal if, for each 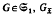is the unique 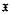-injector of G. 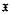is abelian normal if, for each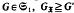. For finite soluble groups these two concepts coincide but the class of Černikov-by-nilpotent -groups is an example of a nonabelian normal Fitting class of -groups. In all known examples in which 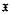-injectors exist 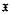is closely associated with some normal Fitting class (the Černikov-by-nilpotent groups arise from studying the locally nilpotent injectors).

Here we investigate normal Fitting classes further, paying particular attention to the distinctions between abelian and nonabelian normal Fitting classes. Products and intersections with (abelian) normal Fitting classes lead to further examples of Fitting classes satisfying the conditions of the existence and conjugacy theorem.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 35 , Issue 2 , June 1992 , pp. 201 - 212
Copyright
Copyright © Edinburgh Mathematical Society 1992

References

REFERENCES

1.Beidleman, J. C. and Brewster, B., Strict normality in Fitting classes I, J. Algebra 51 (1978), 211–217.CrossRefGoogle Scholar
2.Beidleman, J. C., Karbe, M. J. and Tomkinson, M. J., Fitting classes of -groups I, Illinois J. Math. 33 (1989), 333–359.Google Scholar
3.Beidleman, J. C. and Tomkinson, M. J., Fitting classes of -groups, II: Lockett's *-construction, Ricerche Mat. 37 (1988), 283–297.Google Scholar
4.Beidleman, J. C. and Tomkinson, M. J., Hypercentral and nilpotent injectors of -groups, Comm. Algebra 18 (1990), 4307–4321.CrossRefGoogle Scholar
5.Blessenohl, D. and Gaschütz, W., Über normale Schunck- und Fittingklassen, Math. Z. 118 (1970), 1–8.Google Scholar
6.Lausch, H., On normal Fitting classes, Math. Z. 130 (1973), 67–72.CrossRefGoogle Scholar
7.Menegazzo, F. and Newell, M. L., Injectors and Fitting classes of -groups, Atti Acad. Naz. Lined Rend. Cl. Sci. Fis. Mat. Natur. (8) 82 (1988), 629–637.Google Scholar