Hostname: page-component-6bf8c574d5-n2sc8 Total loading time: 0 Render date: 2025-03-09T23:22:38.189Z Has data issue: false hasContentIssue false
  • English
  • Français

A non-periodic indefinite variational problem in ℝN with critical exponent

Part of: Partial differential equations Representations of solutions Elliptic equations and systems

Published online by Cambridge University Press:  26 June 2023

Gustavo S. do Amaral Costa ,
Giovany M. Figueiredo Open the ORCID record for Giovany M. Figueiredo [Opens in a new window]  and
José Carlos de O. Junior Open the ORCID record for José Carlos de O. Junior [Opens in a new window]
Gustavo S. do Amaral Costa
Affiliation:
Departamento de Matemática, Universidade Federal do Maranhão, São Luís, Maranhão, Brazil ([email protected])
Giovany M. Figueiredo
Affiliation:
Departamento de Matemática, Universidade de Brasília, Brasília, Distrito Federal, Brazil ([email protected])
José Carlos de O. Junior
Affiliation:
Colegiado de Matemática, Universidade Federal do Norte do Tocantins, Araguaína, Tocantins, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the non-linear Schrödinger equation(Pμ)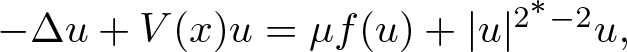

\begin{equation*}\begin{array}{lc}-\Delta u + V(x) u = \mu f(u) + |u|^{2^*-2}u, &\end{array}\end{equation*}
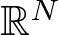in $\mathbb{R}^N$, 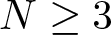$N\geq3$, where V changes sign and 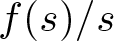$f(s)/s$, s ≠ 0, is bounded, with V non-periodic in x. The existence of a solution is established employing spectral theory, a general linking theorem due to [12] and interaction between translated solutions of the problem at infinity with some qualitative properties of them.

Keywords

critical exponentabstract linking theoremindefinite problemsspectral theory

MSC classification

Primary: 35A15: Variational methods 35J60: Nonlinear elliptic equations 35D30: Weak solutions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 2 , May 2023 , pp. 579 - 612
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, C. O. and Figueiredo, G. M., Multiplicity and Concentration o Positive Solutions for a Class of Quasilinear Problems Adv. Nonlinear Stud. 11 (2011), 265–294.10.1515/ans-2011-0203CrossRefGoogle Scholar
Alves, C. O., and Germano, G. F., Ground state of solution for a class of indefinite variational problems with critical growth, J. Differential Equations 265(1) (2018), 444–447.10.1016/j.jde.2018.02.039CrossRefGoogle Scholar
Berestycki, H. and Lions, P. L., Nonlinear scalar field equations. I. Existence of a ground state, Arch. Ration. Mech. Anal. 82 (1983), 313–345.10.1007/BF00250555CrossRefGoogle Scholar
Chabrowski, J. and Szulkin, A., On a semilinear Schrödinger equation with critical Sobolev exponent, Proc. Amer. Math. Soc. 130 (2001), 85–93.10.1090/S0002-9939-01-06143-3CrossRefGoogle Scholar
Costa, D. G. and Tehrani, H., Existence and multiplicity results for a class of Schrödinger equations with indefinite nonlinearities, Adv. Differential Equations 8 (2003), 1319–1340.10.57262/ade/1355926119CrossRefGoogle Scholar
Egorov, Y. and Kondratiev, V., On Spectral Theorey of Elliptic Operators (Birkhäuser, Basel, 1996).10.1007/978-3-0348-9029-8CrossRefGoogle Scholar
Jeanjean, L., On the existence of bounded Palais-Smale sequences and application to a Landesman-Lazer-type problem set on $\mathbb{R}^N$, Proc. Roy. Soc. Edinburgh Sect. A 129 (1999), 787–809.10.1017/S0308210500013147CrossRefGoogle Scholar
Kryszewski, W. and Szulkin, A., Generalized linking theorem with an application to semilinear Schrödinger equations, Adv. Differential Equations 3 (1998), 441–472.10.57262/ade/1366399849CrossRefGoogle Scholar
Li, G. and Szulkin, A., An asymptotically periodic Schrödinger equation with indefinite linear part, Commun. Contemp. Math. 4 (2002), 763–776.10.1142/S0219199702000853CrossRefGoogle Scholar
Lions, P. L., The concentration-compactness principle in the calculus of variations. The locally compact case. Parts I and II, Ann. Inst. H. Poincaré C Anal. Non Linéaire 1 (1984), .Google Scholar
Maia, L. A., Junior, J. C. O. and Ruviaro, R., A non-periodic and asymptotically linear indefinite variational problem in $\mathbb{R}^N$, Indiana Univ. Math. J. 66(1) (2017), 31–54.10.1512/iumj.2017.66.5955CrossRefGoogle Scholar
Maia, L. A. and Soares, M., An indefinite elliptic problem on RN autonomous at infinity: the crossing effect of the spectrum and the nonlinearity, Calc. Var. Partial Differential Equations 41(59) (2020), 1–22.Google Scholar
Pankov, A. A. and Pflüger, K., On a semilinear Schrödinger equation with periodic potential, Nonlinear Anal. 33 (1998), 593–690.10.1016/S0362-546X(97)00689-5CrossRefGoogle Scholar
Schechter, M. and Zou, W., Weak linking theorems and Schrödinger equations with critical Sobolev exponent, ESAIM Control Optim. Calc. Var. 9 (2003), 601–619.10.1051/cocv:2003029CrossRefGoogle Scholar
Stuart, C. A., An Introduction to Elliptic Equation in RN (River Edge, NJ: World Sci. Publ.), Trieste Notes, (1998).Google Scholar
Stuart, C. A. and Zhou, H. S., Applying the mountain pass theorem to an asymptotically linear elliptic equation on $\mathbb{R}^N$, Comm. Partial Differential Equations 24 (1999), 1731–1758.10.1080/03605309908821481CrossRefGoogle Scholar
Szulkin, A. and Weth, T., Ground state solutions for some indefinite variational problems, J. Func. Anal. 257 (2009), 3802–3822.10.1016/j.jfa.2009.09.013CrossRefGoogle Scholar
Zhang, H., Xu, J. and Zhang, F., On a class of semilinear Schrödinger equation with indefinite linear part, J. Math. Anal. Appl. 414 (2014), 710–724.10.1016/j.jmaa.2014.01.001CrossRefGoogle Scholar