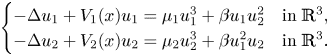Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T15:14:09.101Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-degeneracy of synchronized vector solutions for weakly coupled nonlinear schrödiner systems

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  22 April 2022

Qing Guo  and
Leiga Zhao
Qing Guo
Affiliation:
College of Science, Minzu University of China, Beijing 100081, China ([email protected])
Leiga Zhao
Affiliation:
School of Mathematics and Statistics, Beijing Technology and Business University, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the following two-component Schrödiner system

\[ \begin{cases} -\Delta u_1 +V_1(x) u_1= \mu_1 u_1^{3} +\beta u_1u_2^{2} & \text{in}\;\mathbb{R}^{3},\\ -\Delta u_2+V_2(x) u_2= \mu_2 u_2^{3} +\beta u_1^{2}u_2 & \text{in}\;\mathbb{R}^{3}. \end{cases} \]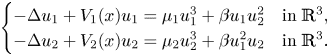
First, we revisit the proof of the existence of an unbounded sequence of non-radial positive vector solutions of synchronized type obtained in S. Peng and Z. Wang [Segregated and synchronized vector solutions for nonlinear Schrödinger systems, Arch. Rational Mech. Anal. 208 (2013), 305–339] to give a point-wise estimate of the solutions. Taking advantage of these estimates, we then show a non-degeneracy result of the synchronized solutions in some suitable symmetric space by use of the locally Pohozaev identities. The main difficulties of BEC systems come from the interspecies interaction between the components, which never appear in the study of single equations. The idea used to estimate the coupling terms is inspired by the characterization of the Fermat points in the famous Fermat problem, which is the main novelty of this paper.

Keywords

Schrödinger systemsNon-degeneracyPopozaev identitiesLyapunov–Schmidt reductionSynchronized solutions

MSC classification

Primary: 35B25: Singular perturbations
Secondary: 35J47: Second-order elliptic systems 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 441 - 459
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosetti, A., Colorado, E. and Ruiz, D., Multi-bump solitons to linearly coupled systems of nonlinear Schrödinger equations, Calculus Variat. 30 (2007), 85–112.CrossRefGoogle Scholar
Bao, W. and Cai, Y., Mathmatical theory and numerical methods for Bose-Einstein condensation, Kinetic Relat. Models 6 (2013), 1–135.CrossRefGoogle Scholar
Guo, Y. and Seiringer, R., On the mass concentration for Bose-Einstein condensates with attractive interactions, Lett. Math. Phys. 104 (2014), 141–156.CrossRefGoogle Scholar
Guo, Y., Zeng, X. and Zhou, H., Energy estimates and symmetry breaking in attractive Bose-Einstein condensates with ring-shaped potentials, Ann. Inst. H. Poincaré Anal. Non Linéaire 33 (2016), 809–828.Google Scholar
Guo, Y., Zeng, X. and Zhou, H., Blow-up solutions for two coupled Gross-Pitaevskii equations with attractive interactions, Discrete Contin. Dyn. Syst. 37 (2017), 3749–3786.CrossRefGoogle Scholar
Guo, Y. X., Peng, S. and Yan, S., Local uniqueness and periodicity induced by concentration, Proc. Lond. Math. Soc. 114 (2017), 1005–1043.CrossRefGoogle Scholar
Guo, Y., Lin, C. and Wei, J., Local uniqueness and refined spike profiles of ground states for two-dimensional attractive Bose-Einstein condensates, SIAM J. Math. Anal. 49 (2017), 3671–3715.CrossRefGoogle Scholar
Guo, Y., Li, S., Wei, J. and Zeng, X., Ground states of two-component attractive Bose-Einstein condensates I: Existence and uniqueness, J. Funct. Anal. 276 (2019), 183–230.CrossRefGoogle Scholar
Guo, Y., Li, S., Wei, J. and Zeng, X., Ground states of two-component attractive Bose-Einstein condensates II: Semi-trivial limit behavior, Trans. Amer. Math. Soc. 371 (2019), 6903–6948.CrossRefGoogle Scholar
Guo, Y., Musso, M., Peng, S. and Yan, S., Non-degeneracy and existence of new solutions for the Schrödinger equations, preprint (2021).CrossRefGoogle Scholar
Lin, T. and Wei, J., Ground state of N coupled nonlinear Schrödinger equations in $\mathbb {R}^{N}$, $N\leq 3$., Comm. Math. Phys. 255 (2005), 629–653.CrossRefGoogle Scholar
Long, W. and Peng, S., Segregated vector solutions for a class of Bose-Einstein systems, J. Differ. Equ. 257 (2014), 207–230.CrossRefGoogle Scholar
Luo, P., Peng, S. and Yan, S., Excited states on Bose-Einstein condensates with attractive interactions.Google Scholar
Noussair, E. and Yan, S., On positive multipeak solutions of a nonlinear elliptic problem, J. Lond. Math. Soc. 62 (2000), 213–227.CrossRefGoogle Scholar
Peng, S. and Wang, Z., Segregated and synchronized vector solutions for nonlinear Schrödinger systems, Arch. Rational Mech. Anal. 208 (2013), 305–339.CrossRefGoogle Scholar
Royo-Letelier, J., Segregation and symmetry breaking of strongly coupled two component Bose-Einstein condensates in a harmonic trap, Calc. Var. Partial Differ. Equ. 49 (2014), 103–124.CrossRefGoogle Scholar