Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-16T07:42:16.908Z Has data issue: false hasContentIssue false
  • English
  • Français

The nonabelian product modulo sum

Part of: Special aspects of infinite or finite groups Foundations Homotopy groups Set theory

Published online by Cambridge University Press:  11 April 2025

Samuel M. Corson Open the ORCID record for Samuel M. Corson [Opens in a new window]
Samuel M. Corson*
Affiliation:
E. T. S. I. I. Universidad Politecnica de Madrid, Jose Gutierrez Abascal 2, 28006 Madrid, Spain
*
Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that if 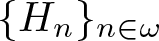$\{H_n\}_{n \in \omega}$ is a sequence of groups without involutions, with $1 \lt |H_n| \leq 2^{\aleph_0}$, then the topologist’s product modulo the finite words is (up to isomorphism) independent of the choice of sequence. This contrasts with the abelian setting: if $\{A_n\}_{n \in \omega}$ is a sequence of countably infinite torsion-free abelian groups, then the isomorphism class of the product modulo sum $\prod_{n \in \omega} A_n/\bigoplus_{n \in \omega} A_n$ is dependent on the sequence.

Keywords

Algebraically compact groupinfinite wordtopologist’s product

MSC classification

Primary: 03E75: Applications of set theory 20A15: Applications of logic to group theory 55Q52: Homotopy groups of special spaces
Secondary: 20F10: Word problems, other decision problems, connections with logic and automata 20F34: Fundamental groups and their automorphisms
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 41
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bogley, W. A., Sieradski, A. J., Weighted combinatorial group theory and wild metric complexes, Groups-Korea’98 (Pusan), de Gruyter, Berlin, 2000, 53–80.Google Scholar
Conner, G. R., Hojka, W., Meilstrup, M., Archipelago groups, Proc. Amer. Math. Soc. 143 (2015), 4973–4988.CrossRefGoogle Scholar
Corson, S., The Griffiths double cone group is isomorphic to the triple, Pac. J. Math. 327 (2023), 297–336.CrossRefGoogle Scholar
Eda, K., Free σ-products and noncommutatively slender groups, J. Algebra 148 (1992), 243–263.CrossRefGoogle Scholar
Eda, K., Free subgroups of the fundamental group of the Hawaiian earring, J. Algebra 219 (1999), 598–605.CrossRefGoogle Scholar
Fuchs, L., Abelian Groups, Springer, London, 2015.CrossRefGoogle Scholar
Griffiths, H., The fundamental group of two spaces with a common point, Quart. J. Math. Oxford 2 (1954), 175–190.CrossRefGoogle Scholar
Hojka, W., The harmonic archipelago as a universal locally free group, J. Algebra 437 (2015), 44–51.CrossRefGoogle Scholar
Ol’shanskii, A. Yu., Geometry of Defining Relations in Groups, Kluwer Academic Publisher (1991).CrossRefGoogle Scholar
Rosenstein, J. G., Linear Orderings, New York: Academic Press (1982)Google Scholar