Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T12:26:34.407Z Has data issue: false hasContentIssue false
  • English
  • Français

The near-rings hosted by a class of groups

Published online by Cambridge University Press:  20 January 2009

R. R. Laxton  and
R. Lockhart
R. R. Laxton
Affiliation:
University of Nottingham
R. Lockhart
Affiliation:
University of Nottingham
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Clay (3), Johnson (5) and Krimmel (6) have each considered the near-rings with identity on dihedral groups. Krimmel actually generalised the class of dihedral groups and investigated the class of finite non-abelian groups with a cyclic normal subgroup of prime index: we shall call this class 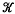. Krimmel considered the near-rings with identity that might be denned on members of 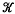and he determined the subclass of groups in 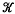which support near-rings of this kind. He also managed to calculate the number of non-isomorphic near-rings involved for certain cases. His methods were essentially combinatorial, and his results were expressed in terms of various integers which characterised the individual members of 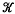. Certain features of this work led us to investigate the structure of near-rings on members of 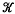from a more algebraic point of view and thereby to complete and extend Krimmel's programme. Part of the work in this paper formed the basis of the second author's thesis (7). We should like to thank Dr. J. Krimmel for permission to include some of his results, and Dr. J. Meldrum who detected an error in our original formulation of Theorem 7.1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 23 , Issue 1 , February 1980 , pp. 69 - 86
Copyright
Copyright © Edinburgh Mathematical Society 1980

References

REFERENCES

(1) Betsch, G., Primitive Near-Rings, Math. Z. 130 (1973), 351–361.CrossRefGoogle Scholar
(2) Clay, J. R., The Near-Rings on Groups of Low Order, Math. Z. 104 (1968), 364–371.CrossRefGoogle Scholar
(3) Clay, J. R., Research into Near-Ring Theory using a digital computer, B.I.T. 104 10 (1970), 249–265.Google Scholar
(4) Hall, M., The Theory of Groups (Macmillan, 1973).Google Scholar
(5) Johnson, M., Near-Rings with identities on Dihedral Groups, Proc. Edinburgh Math. Soc. (2) 18 (1973), 219–228.CrossRefGoogle Scholar
(6) Conditions on Near-Rings with identity and the near-ring with identity on some meta-cyclic groups (Doctoral dissertation, Univ. of Arizona, Tucson, 1972).Google Scholar
(7) Lockhart, R., Near-Rings on a class of Groups (Doctoral dissertation, Univ. of Nottingham, 1977).Google Scholar