Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T19:41:05.737Z Has data issue: false hasContentIssue false
  • English
  • Français

N-ary Transformations of Sequences

Published online by Cambridge University Press:  20 January 2009

A. V. Boyd
A. V. Boyd
Affiliation:
Department of Mathematics, University of the Witwatersrand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T(α1, α2, …, αn−1) be the n-ary transformation which takes the sequence {si}, (i = 0, 1, …), into the sequence {s'i} where

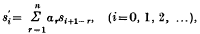
with sm = 0 when m is a negative integer, and where α1, …, αn an are real numbers with sum unity. In a previous note (1) conditions were found on α and β for the ternary transformation T(α, β) to be equivalent to convergence. A method is given here for treating the similar problem for the general n-ary transformation.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 11 , Issue 4 , November 1959 , pp. 221 - 222
Copyright
Copyright © Edinburgh Mathematical Society 1959

References

REFERENCES

Borwein, D. and Boyd, A. V., Binary and ternary transformations of sequences, Proc. Edin. Math. Soc, 11 (1959), 175–181.CrossRefGoogle Scholar
Wall, H. S., Analytic Theory of Continued Fractions, New York, 1948.Google Scholar