Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oleinik, V. L.
and
Vuorinen, M.
1991.
Embedding theorems for Bergman spaces in quasiconformal balls.
Manuscripta Mathematica,
Vol. 72,
Issue. 1,
p.
181.
Mateljević, M.
and
Pavlović, M.
1993.
An extension of the Forelli–Rudin projection theorem.
Proceedings of the Edinburgh Mathematical Society,
Vol. 36,
Issue. 3,
p.
375.
Gu, Dangsheng
1993.
A carleson measure theorem for weighted bergman spaces.
Complex Variables, Theory and Application: An International Journal,
Vol. 21,
Issue. 1-2,
p.
79.
Ortega-Cerdà, Joaquim
1998.
Zero sets of holomorphic functions in the bidisk.
Arkiv för Matematik,
Vol. 36,
Issue. 1,
p.
103.
Wu, Zhijian
and
Yang, Liming
1998.
Multipliers between Dirichlet spaces.
Integral Equations and Operator Theory,
Vol. 32,
Issue. 4,
p.
482.
Wu, Zhijian
1999.
Carleson Measures and Multipliers for Dirichlet Spaces.
Journal of Functional Analysis,
Vol. 169,
Issue. 1,
p.
148.
Domenig, Thomas
1999.
Composition Operators Belonging to Operator Ideals.
Journal of Mathematical Analysis and Applications,
Vol. 237,
Issue. 1,
p.
327.
Wu, Zhijian
1999.
Clifford Analysis and Commutators on the Besov Spaces.
Journal of Functional Analysis,
Vol. 169,
Issue. 1,
p.
121.
Oleinik, Vladimir L.
2000.
Complex Analysis, Operators, and Related Topics.
p.
269.
Choe, Boo
Koo, Hyungwoon
and
Smith, Wayne
2003.
Composition operators acting on holomorphic Sobolev spaces.
Transactions of the American Mathematical Society,
Vol. 355,
Issue. 7,
p.
2829.
Hu, Zhangjian
2004.
Extended Cesàro operators on Bergman spaces.
Journal of Mathematical Analysis and Applications,
Vol. 296,
Issue. 2,
p.
435.
Choe, Boo R.
Lee, Young J.
and
Na, Kyunguk
2004.
Positive Toeplitz operators from a harmonic Bergman space into another.
Tohoku Mathematical Journal,
Vol. 56,
Issue. 2,
Manhas, J. S.
2007.
Composition Operators and Multiplication Operators on Weighted Spaces of Analytic Functions.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2007,
Issue. ,
p.
1.
Luo, Luo
and
Ueki, Sei-ichiro
2007.
Weighted composition operators between weighted Bergman spaces and Hardy spaces on the unit ball of Cn.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
88.
Nishio, Masaharu
Suzuki, Noriaki
and
Yamada, Masahiro
2008.
Interpolating Sequences of Parabolic Bergman Spaces.
Potential Analysis,
Vol. 28,
Issue. 4,
p.
357.
Nishio, Masaharu
Suzuki, Noriaki
and
Yamada, Masahiro
2010.
Carleson inequalities on parabolic Bergman spaces.
Tohoku Mathematical Journal,
Vol. 62,
Issue. 2,
Li, Songxiao
and
Shamoyan, Romi
2010.
On some estimates and Carleson type measure for multifunctional holomorphic spaces in the unit ball.
Bulletin des Sciences Mathématiques,
Vol. 134,
Issue. 2,
p.
144.
Sehba, Benoît Florent
and
Engler, Hans
2011.
p‐Carleson Measures for a Class of Hardy‐Orlicz Spaces.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2011,
Issue. 1,
Saukko, Erno
2011.
Difference of composition operators between standard weighted Bergman spaces.
Journal of Mathematical Analysis and Applications,
Vol. 381,
Issue. 2,
p.
789.
Saukko, Erno
2012.
An application of atomic decomposition in Bergman spaces to the study of differences of composition operators.
Journal of Functional Analysis,
Vol. 262,
Issue. 9,
p.
3872.


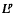 will denote the usual Lebesgue space with respect to
will denote the usual Lebesgue space with respect to 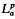 . Let μ be some positivefinite Borel measure on
. Let μ be some positivefinite Borel measure on