Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T00:26:57.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiparameter spectral theory and Taylor's joint spectrum in Hilbert space

Published online by Cambridge University Press:  20 January 2009

B. P. Rynne
B. P. Rynne
Affiliation:
Department of MathematicsUniversity of YorkHeslingtonYork YO1 5DD
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let n≧1 be an integer and suppose that for each i= 1,…,n, we have a Hilbert space Hi and a set of bounded linear operators Ti, Vij:Hi→Hi, j=1,…,n. We define the system of operators

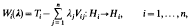
where λ=(λ1,…,λn)∈ℂn. Coupled systems of the form (1.1) are called multiparameter systems and the spectral theory of such systems has been studied in many recent papers. Most of the literature on multiparameter theory deals with the case where the operators Ti and Vij are self-adjoint (see [14]). The non self-adjoint case, which has received relatively little attention, is discussed in [12] and [13].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 31 , Issue 1 , February 1988 , pp. 127 - 144
Copyright
Copyright © Edinburgh Mathematical Society 1988

References

REFERENCES

1.Almamedov, M. S. and Isaev, G. A., Solvability of nonselfadjoint linear operator systems and the set of decomposability of multiparameter spectral problems, Soviet. Math. Dokl. 31 (1986), 472–474.Google Scholar
2.Atkinson, F. V., Multiparameter Eigenvalue Problems Vol I: Matrices and Compact Operators (Academic Press, New York, 1972).Google Scholar
3.Binding, P. A. and Browne, P. J., A variational approach to multiparameter eigenvalue problems in Hilbert space, SIAM J. Math. Anal. 9 (1978), 1054–1067.CrossRefGoogle Scholar
4.Ceausescu, Z. and Vasilescu, F. H., Tensor products and the joint spectrum in Hilbert spaces, Proc. Amer. Math. Soc. 72 (1978), 505–508.CrossRefGoogle Scholar
5.Cho, M. and Takaguchi, M., Identity of Taylor's joint spectrum and Dash's joint spectrum, Studia Math. 70 (1982), 225–229.CrossRefGoogle Scholar
6.Dash, A. T., Joint spectra, Studia Math. 45 (1973), 225–237.CrossRefGoogle Scholar
7.Kallstrom, A., Joint spectra and multiparameter eigenvalue problems, in Multiparameter Problems, ed. Roach, G. F. (University of Strathclyde Seminars in Applied Mathematical Analysis, Shiva, 1984).Google Scholar
8.Kallstrom, A. and Sleeman, B. D., Solvability of a linear operator system, J. Math. Anal. Appl. 55(1976), 785–793.CrossRefGoogle Scholar
9.Khelemskii, A. Ya., Homological methods in Taylor's holomorphic calculus of several operators in a Banach space, Russian Math. Surveys 36 (1981), 139–192.CrossRefGoogle Scholar
10.MacLane, S., Homology (Springer-Verlag, Berlin, 1963).CrossRefGoogle Scholar
11.MacLane, S. and Birkoff, G., Algebra (MacMillan, New York, 1967).Google Scholar
12.McGhee, D. F. and Roach, G. F., The spectrum of multiparameter problems in Hilbert space, Proc. Roy. Soc. Edinburgh 91A (1981), 31–42.CrossRefGoogle Scholar
13.McGhee, D. F., Multiparameter problems and joint spectra, Proc. Roy. Soc. Edinburgh 93A (1982), 129–135.CrossRefGoogle Scholar
14.Sleeman, B. D., Multiparameter Spectral Theory in Hilbert Space (Pitman, London, 1978).CrossRefGoogle Scholar
15.Taylor, A. E. and Lay, D. C., Introduction to Functional Analysis (Wiley, New York, 1980).Google Scholar
16.Taylor, J. L., A joint spectrum for several commuting operators, J. Funct. Anal. 6 (1970), 172–191.CrossRefGoogle Scholar
17.Taylor, J. L., The analytic functional calculus for several commuting operators, Acta. Math. 125 (1970), 1–38.CrossRefGoogle Scholar