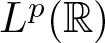1. Introduction
The Lebesgue differentiation theorem states that, for a function ![]() $f \in L^1_{loc}({\mathbb R}^d),$ there is a null set
$f \in L^1_{loc}({\mathbb R}^d),$ there is a null set ![]() $E \subset {\mathbb R}^d$ so that, if
$E \subset {\mathbb R}^d$ so that, if ![]() $x \in {\mathbb R}^d \setminus E,$ then
$x \in {\mathbb R}^d \setminus E,$ then
 \begin{equation*}
\lim_{r \to 0} \frac{1}{|B_r(0)|} \int_{B_r(x)} f(y) \, dy = f(x).
\end{equation*}
\begin{equation*}
\lim_{r \to 0} \frac{1}{|B_r(0)|} \int_{B_r(x)} f(y) \, dy = f(x).
\end{equation*}A natural question, in that regard, is whether the same convergence holds if one replaces averages over balls by averages over spheres. In addition, the study of such spherical averages is deeply connected with the study of dimension-free bounds for the Hardy–Littlewood maximal function, as highlighted by Stein [Reference Stein31].
In this direction, such a theorem on spherical averages induces the study of the spherical maximal function defined by:
 \begin{equation}
S (f) (x) := \sup_{t \gt 0}\left| \int_{\mathbb S^{n-1}}f(x-t y) d\sigma_{n-1}(y)\right|.
\end{equation}
\begin{equation}
S (f) (x) := \sup_{t \gt 0}\left| \int_{\mathbb S^{n-1}}f(x-t y) d\sigma_{n-1}(y)\right|.
\end{equation} The study of bounds for the spherical maximal function was initiated by Stein [Reference Stein30], who obtained its boundedness from ![]() $L^p(\mathbb R^n) \to L^p(\mathbb R^n)$ when
$L^p(\mathbb R^n) \to L^p(\mathbb R^n)$ when ![]() $n\geq 3$ and
$n\geq 3$ and ![]() $p \gt \frac{n}{n-1}$ and showed that it is unbounded when
$p \gt \frac{n}{n-1}$ and showed that it is unbounded when ![]() $p\leq\frac{n}{n-1}$ and
$p\leq\frac{n}{n-1}$ and ![]() $n\geq 2$. The analogue of this result in dimension n = 2 was established later by Bourgain in [Reference Bourgain6], who also obtained a restricted weak type estimate in [Reference Bourgain5] in the case
$n\geq 2$. The analogue of this result in dimension n = 2 was established later by Bourgain in [Reference Bourgain6], who also obtained a restricted weak type estimate in [Reference Bourgain5] in the case ![]() $n\geq 3$.
$n\geq 3$.
Further developments have been obtained by Seeger, Tao, and Wright, which, in [Reference Seeger, Tao and Wright29], proved that the restricted weak type estimate does not hold in dimension n = 2. A number of other authors have also studied the spherical maximal function, among which we highlight [Reference Bak, Oberlin and Seeger3, Reference Carbery9, Reference Cowling and Mauceri11, Reference Mockenhaupt, Seeger and Sogge25, Reference Rubio de Francia27, Reference Schlag28] and the references therein. Extensions of the spherical maximal function to different settings have also been established by several authors; for instance, see [Reference Calderon8, Reference Duoandikoetxea and Vega14, Reference Greenleaf20, Reference Magyar, Stein and Wainger24].
The main object of this work is the m-linear analogue of the spherical maximal function, given by:
 \begin{equation}
S^m (f_1,\dots,f_m) (x) := \sup_{t \gt 0}\left| \int_{\mathbb S^{mn-1}} \prod_{j=1}^{m} f_j(x-t y^j) d\sigma_{mn-1}(y^1,\dots,y^m)\right|,
\end{equation}
\begin{equation}
S^m (f_1,\dots,f_m) (x) := \sup_{t \gt 0}\left| \int_{\mathbb S^{mn-1}} \prod_{j=1}^{m} f_j(x-t y^j) d\sigma_{mn-1}(y^1,\dots,y^m)\right|,
\end{equation} defined originally for Schwartz functions, where ![]() $d\sigma$ stands for the (normalized) surface measure of
$d\sigma$ stands for the (normalized) surface measure of ![]() $\mathbb S^{mn-1}$.
$\mathbb S^{mn-1}$.
The m = 2 case of (2) is called the bi(sub)linear spherical maximal function, and it was first introduced by Geba, Greenleaf, Iosevich, Palsson, and Sawyer [Reference Geba, Greenleaf, Iosevich, Palsson and Sawyer16], who obtained the first bounds for it. Later improved bounds were provided by [Reference Barrionuevo, Grafakos, He, Honzík and Oliveira4, Reference Grafakos, He and Honzík18, Reference Heo, Hong and Yang21, Reference Jeong and Lee22]. A multilinear (non-maximal) version of this operator when all input functions lie in the same space ![]() $L^{p}({\mathbb R})$ was previously studied by Oberlin [Reference Oberlin26].
$L^{p}({\mathbb R})$ was previously studied by Oberlin [Reference Oberlin26].
It was not until the work of Jeong and Lee [Reference Jeong and Lee22] that the sharp open range of boundedness would be proved for the bilinear operator. Indeed, the authors proved in [Reference Jeong and Lee22] that when ![]() $n\geq 2$, the bilinear maximal function is pointwise bounded by the product of the linear spherical maximal function and the Hardy–Littlewood maximal function, which implies boundedness in the optimal open set of exponents. This was generalized to the multilinear setting in [Reference Dosidis12]. See also [Reference Anderson and Palsson1, Reference Anderson and Palsson2, Reference Borges, Foster, Ou, Pipher and Zhou7, Reference Dosidis and Grafakos13] for further developments.
$n\geq 2$, the bilinear maximal function is pointwise bounded by the product of the linear spherical maximal function and the Hardy–Littlewood maximal function, which implies boundedness in the optimal open set of exponents. This was generalized to the multilinear setting in [Reference Dosidis12]. See also [Reference Anderson and Palsson1, Reference Anderson and Palsson2, Reference Borges, Foster, Ou, Pipher and Zhou7, Reference Dosidis and Grafakos13] for further developments.
The purpose of this work is to complement the results of [Reference Dosidis12, Reference Jeong and Lee22] in the n = 1 case. The spherical maximal operators are generally more singular when the dimension is smaller, which is reflected by the fact that the decay of the Fourier transform of the surface measure is smaller in low dimensions.
When ![]() $n\geq 2$, where the optimal boundedness range of the bilinear operator is
$n\geq 2$, where the optimal boundedness range of the bilinear operator is ![]() $p \gt \frac{n}{2n-1}$. The optimality of the condition is found in [Reference Grafakos, He and Honzík18] and yields the necessary condition p > 1 when n = 1. However, as was shown by Heo, Hong, and Yang in [Reference Heo, Hong and Yang21], when n = 1 the conditions
$p \gt \frac{n}{2n-1}$. The optimality of the condition is found in [Reference Grafakos, He and Honzík18] and yields the necessary condition p > 1 when n = 1. However, as was shown by Heo, Hong, and Yang in [Reference Heo, Hong and Yang21], when n = 1 the conditions ![]() $p_1,p_2\geq 2$ are also necessary which further restricts the possible boundedness range.
$p_1,p_2\geq 2$ are also necessary which further restricts the possible boundedness range.
Our first result establishes the ![]() $L^{p_1}\times L^{p_2}\to L^p$ boundedness of the one-dimensional bilinear operator (m = 2) in the region
$L^{p_1}\times L^{p_2}\to L^p$ boundedness of the one-dimensional bilinear operator (m = 2) in the region ![]() $p_1,p_2 \gt 2$ (see Figure 1). We show that this range is optimal via a modification of the counterexample in [Reference Heo, Hong and Yang21], which excludes the possibility of even a weak-type bound when p 1 or p 2 equals 2.
$p_1,p_2 \gt 2$ (see Figure 1). We show that this range is optimal via a modification of the counterexample in [Reference Heo, Hong and Yang21], which excludes the possibility of even a weak-type bound when p 1 or p 2 equals 2.
Theorem 1. Let ![]() $p_1,p_2 \gt 1$ and
$p_1,p_2 \gt 1$ and  $p=\frac{p_1p_2}{p_1+p_2}$. Then, there is a constant
$p=\frac{p_1p_2}{p_1+p_2}$. Then, there is a constant ![]() $C=C(p_1,p_2) \lt \infty$ such that:
$C=C(p_1,p_2) \lt \infty$ such that:

Figure 1. Range of ![]() $L^{p_1}\times L^{p_2}\to L^p$ boundedness of
$L^{p_1}\times L^{p_2}\to L^p$ boundedness of ![]() $S^2(f,g)$, when n = 1.
$S^2(f,g)$, when n = 1.
if and only if ![]() $p_1,p_2 \gt 2$. In this case S 2 admits a unique bounded extension from
$p_1,p_2 \gt 2$. In this case S 2 admits a unique bounded extension from ![]() $L^{p_1}({\mathbb R})\times L^{p_2}({\mathbb R})$ to
$L^{p_1}({\mathbb R})\times L^{p_2}({\mathbb R})$ to ![]() $L^{p}({\mathbb R})$.
$L^{p}({\mathbb R})$.
Moreover, for the end-point cases ![]() $p_1=2$ and
$p_1=2$ and ![]() $p_2=2$ the bilinear spherical maximal function S 2 fails to be weak type bounded. In particular, for any
$p_2=2$ the bilinear spherical maximal function S 2 fails to be weak type bounded. In particular, for any ![]() $1\leq p_1,p_2\leq \infty$,
$1\leq p_1,p_2\leq \infty$,  $\frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{p}$, S 2 does not boundedly map
$\frac{1}{p_1}+\frac{1}{p_2}=\frac{1}{p}$, S 2 does not boundedly map ![]() $L^2\times L^{p_2}\to L^{p,\infty}$ nor
$L^2\times L^{p_2}\to L^{p,\infty}$ nor ![]() $L^{p_1}\times L^2\to L^{p,\infty}$.
$L^{p_1}\times L^2\to L^{p,\infty}$.
The boundedness result of Theorem 1 was also obtained independently by Christ and Zhou in [Reference Christ and Zhou10], where the lacunary operator, with the supremum taken over the set ![]() $t\in\{2^k\,:\,k\in{\mathbb Z}\}$, is also treated.
$t\in\{2^k\,:\,k\in{\mathbb Z}\}$, is also treated.
The proof of this result is based on a decomposition of the circle into sectors, in which we may safely parametrize it. We then use the curvature of the circle in our favour, in order to show a different kind of pointwise domination with respect to the ![]() $n \ge 2$ case: instead of bounding pointise by a product of the Hardy–Littlewood and spherical maximal functions, we obtain bounds with products of suitable p-maximal functions. In order to obtain these bounds, the curvature helps us by allowing us to insert power weights into the strategy, which effectively enable us to ‘transfer’ decay from one maximal function to the other.
$n \ge 2$ case: instead of bounding pointise by a product of the Hardy–Littlewood and spherical maximal functions, we obtain bounds with products of suitable p-maximal functions. In order to obtain these bounds, the curvature helps us by allowing us to insert power weights into the strategy, which effectively enable us to ‘transfer’ decay from one maximal function to the other.
Our second result deals with the multilinear case ![]() $m\geq 3$. Using the coarea formula (see [Reference Federer15, Theorem 3.2.22]), we see that the following pointwise bound holds, for fixed t > 0:
$m\geq 3$. Using the coarea formula (see [Reference Federer15, Theorem 3.2.22]), we see that the following pointwise bound holds, for fixed t > 0:
 \begin{align*} & \left| S^m_t(f_1,\dots,f_m)(x) \right| = \left| \int_{S^{m-1}} \prod_{k=1}^m f_k(x-ty_k) d\sigma(y) \right| \\
&= \left| \int_{{\mathbb B}^{m-2}}\prod_{k=3}^m f_k(x-ty_k) \int_{r_y\mathbb{S}^1} f_1(x-ty_1)f_2(x-ty_2) d\sigma(y_1,y_2) \frac{dy_3\cdots dy_m}{r_y} \right| \\
&\leq \left| \int_{{\mathbb B}^{m-2}}\prod_{k=3}^m f_k(x-ty_k) \int_{\mathbb{S}^1} f_1(x-tr_y y_1)f_2(x-tr_y y_2) d\sigma(y_1,y_2) dy_3\cdots dy_m \right| \\
&\leq S^2(f_1,f_2)(x) \cdot M^{m-2}(f_3,\cdots,f_m)(x),
\end{align*}
\begin{align*} & \left| S^m_t(f_1,\dots,f_m)(x) \right| = \left| \int_{S^{m-1}} \prod_{k=1}^m f_k(x-ty_k) d\sigma(y) \right| \\
&= \left| \int_{{\mathbb B}^{m-2}}\prod_{k=3}^m f_k(x-ty_k) \int_{r_y\mathbb{S}^1} f_1(x-ty_1)f_2(x-ty_2) d\sigma(y_1,y_2) \frac{dy_3\cdots dy_m}{r_y} \right| \\
&\leq \left| \int_{{\mathbb B}^{m-2}}\prod_{k=3}^m f_k(x-ty_k) \int_{\mathbb{S}^1} f_1(x-tr_y y_1)f_2(x-tr_y y_2) d\sigma(y_1,y_2) dy_3\cdots dy_m \right| \\
&\leq S^2(f_1,f_2)(x) \cdot M^{m-2}(f_3,\cdots,f_m)(x),
\end{align*} where ![]() ${\mathbb B}^{\kappa}$ stands for the unit ball in
${\mathbb B}^{\kappa}$ stands for the unit ball in ![]() ${\mathbb R}^\kappa$,
${\mathbb R}^\kappa$,
 \begin{equation*}
M^m(f_1,\cdots,f_m)(x) = \sup_{t \gt 0} \int_{{\mathbb B}^{m}} \prod_{i=1}^m |f_i(x-ty_i)| dy_1\cdots d_m,
\end{equation*}
\begin{equation*}
M^m(f_1,\cdots,f_m)(x) = \sup_{t \gt 0} \int_{{\mathbb B}^{m}} \prod_{i=1}^m |f_i(x-ty_i)| dy_1\cdots d_m,
\end{equation*} is the m-(sub)linear Hardy–Littlewood maximal function (first defined in [Reference Lerner, Ombrosi, Pérez, Torres and Trujillo-González23]), and  $r_y=\sqrt{1-\sum_{k=3}^m y_k^2}$. Since M m is pointwise bounded by the product of m Hardy–Littlewood maximal functions (denoted
$r_y=\sqrt{1-\sum_{k=3}^m y_k^2}$. Since M m is pointwise bounded by the product of m Hardy–Littlewood maximal functions (denoted ![]() $Mf:= M^1 f$), we arrive at the following estimates:
$Mf:= M^1 f$), we arrive at the following estimates:
 \begin{equation}
\left| S^m_t(f_1,\dots,f_m)(x) \right| \lesssim S^2(f_{i_1},f_{i_2})(x) \prod_{j\neq i_1,i_2} M(f_j)(x),
\end{equation}
\begin{equation}
\left| S^m_t(f_1,\dots,f_m)(x) \right| \lesssim S^2(f_{i_1},f_{i_2})(x) \prod_{j\neq i_1,i_2} M(f_j)(x),
\end{equation} using the fact that the operator Sm is symmetric with respect to permutations of the functions fi. From these estimates and interpolation, we obtain ![]() $L^{p_1}\times\cdots\times L^{p_m} \to L^p$ boundedness for Sm in a certain range of exponents (see Figure 2). The range of exponents thus obtained turns out to be the optimal for the strong-type bounds. Unlike Theorem 1 our counterexamples here do not exclude the possibility of weak-type bounds on parts of the boundary; we discuss this point at the end of the section.
$L^{p_1}\times\cdots\times L^{p_m} \to L^p$ boundedness for Sm in a certain range of exponents (see Figure 2). The range of exponents thus obtained turns out to be the optimal for the strong-type bounds. Unlike Theorem 1 our counterexamples here do not exclude the possibility of weak-type bounds on parts of the boundary; we discuss this point at the end of the section.

Figure 2. The ![]() $L^{p_1}\times L^{p_2}\times L^{p_3}\to L^p$ boundedness region of the trilinear spherical maximaloperator (n = 1).
$L^{p_1}\times L^{p_2}\times L^{p_3}\to L^p$ boundedness region of the trilinear spherical maximaloperator (n = 1).
Theorem 2. Let n = 1, ![]() $m\geq 2$,
$m\geq 2$, ![]() $1\leq p_i\leq \infty$ for
$1\leq p_i\leq \infty$ for ![]() $i=1,\dots,m$, and
$i=1,\dots,m$, and  $\displaystyle\frac{1}{p} = \sum_{i=1}^m\frac1{p_i}$. Then there is a constant
$\displaystyle\frac{1}{p} = \sum_{i=1}^m\frac1{p_i}$. Then there is a constant ![]() $C \lt \infty$, only depending on
$C \lt \infty$, only depending on ![]() $p_1,\dots,p_m$, such that
$p_1,\dots,p_m$, such that
 \begin{equation}\|S^m(f_1,\dots,f_m)\|_{L^p({\mathbb R})}\leq C\prod_{i=1}^m \|f_i\|_{L^{p_i}({\mathbb R})},
\end{equation}
\begin{equation}\|S^m(f_1,\dots,f_m)\|_{L^p({\mathbb R})}\leq C\prod_{i=1}^m \|f_i\|_{L^{p_i}({\mathbb R})},
\end{equation} for all Schwartz functions fi, ![]() $i=1,\dots,m$ if and only if all three of the following conditions hold:
$i=1,\dots,m$ if and only if all three of the following conditions hold:
a)
 $\displaystyle\frac{1}{p} = \sum_{i=1}^m\frac1{p_i} \lt m-1$,
$\displaystyle\frac{1}{p} = \sum_{i=1}^m\frac1{p_i} \lt m-1$,b) for every
 $i=1,\dots,m$,
$i=1,\dots,m$,  $\displaystyle{\sum_{j\neq i}\frac1{p_j}} \lt m-\frac32$,
$\displaystyle{\sum_{j\neq i}\frac1{p_j}} \lt m-\frac32$,c)
 $\big(\frac1{p_1},\dots\frac{1}{p_m}\big) \not\in \{0,1\}^{m} \setminus\{(0,\dots,0)\}$.
$\big(\frac1{p_1},\dots\frac{1}{p_m}\big) \not\in \{0,1\}^{m} \setminus\{(0,\dots,0)\}$.
Additionally, if  $\big(\frac1{p_1},\dots\frac{1}{p_m}\big) \in \{0,1\}^m \setminus\{(0,\dots,0)\}$, then we have the weak-type bound
$\big(\frac1{p_1},\dots\frac{1}{p_m}\big) \in \{0,1\}^m \setminus\{(0,\dots,0)\}$, then we have the weak-type bound
 \begin{equation}\|S^m(f_1,\dots,f_m)\|_{L^{p,\infty}({\mathbb R})}\leq C\prod_{i=1}^m \|f_i\|_{L^{p_i}({\mathbb R})},
\end{equation}
\begin{equation}\|S^m(f_1,\dots,f_m)\|_{L^{p,\infty}({\mathbb R})}\leq C\prod_{i=1}^m \|f_i\|_{L^{p_i}({\mathbb R})},
\end{equation} for some constant ![]() $C=C(p_1,\dots,p_m)$ if and only if (a) and (b) both hold.
$C=C(p_1,\dots,p_m)$ if and only if (a) and (b) both hold.
As an example we graph the region of boundedness for the trilinear spherical maximal function.
In order to prove the necessity of the conditions on the exponents in Theorem 2, we shall employ two different kinds of counterexamples: the first is where all functions involved are similarly concentrated around the origin, which gives us condition (a), and the second in which all but one function – at entry i – are similarly concentrated around the origin, whereas fi is spread out; this gives us condition (b). A modification of such examples in the spirit of Stein’s original counterexample allows us to obtain condition (c) and the asserted lack of endpoint bounds.
Finally, let us mention for a brief moment the boundary case: for shortness of notation, define, for ![]() $i=1,\dots,m$, the sets
$i=1,\dots,m$, the sets ![]() $\mathcal H , \mathcal H_i$ as:
$\mathcal H , \mathcal H_i$ as:
 \begin{equation*}\mathcal H := [0,1]^m \cap \bigg\{\sum_{j=1}^m x_j = m-1\bigg\} \bigcap\left[ \bigcap_{i=1}^m\Big\{\sum_{j\neq i} x_j \leq m-\frac32\Big\}\right], \end{equation*}
\begin{equation*}\mathcal H := [0,1]^m \cap \bigg\{\sum_{j=1}^m x_j = m-1\bigg\} \bigcap\left[ \bigcap_{i=1}^m\Big\{\sum_{j\neq i} x_j \leq m-\frac32\Big\}\right], \end{equation*}and
 \begin{equation*}\mathcal{H}_i = [0,1]^m \cap \bigg\{\sum_{j\neq i} x_j = m-\frac32\bigg\}\bigcap \Big\{\sum_{j=1}^m x_j \leq m-1\Big\}.\end{equation*}
\begin{equation*}\mathcal{H}_i = [0,1]^m \cap \bigg\{\sum_{j\neq i} x_j = m-\frac32\bigg\}\bigcap \Big\{\sum_{j=1}^m x_j \leq m-1\Big\}.\end{equation*} In the diagram above, the set ![]() $\mathcal{H}$ denotes the middle triangle in red, whereas each of the
$\mathcal{H}$ denotes the middle triangle in red, whereas each of the ![]() $\mathcal{H}_i,i=1,2,3,$ denote one of the red rectangles. In spite of Theorem 2 and the counterexamples it provides, the question of weak-type boundedness of Sm when
$\mathcal{H}_i,i=1,2,3,$ denote one of the red rectangles. In spite of Theorem 2 and the counterexamples it provides, the question of weak-type boundedness of Sm when  $(\frac1{p_1},\dots,\frac1{p_m})$ belongs in
$(\frac1{p_1},\dots,\frac1{p_m})$ belongs in ![]() $\mathcal H$ or
$\mathcal H$ or ![]() $\mathcal H_i$ remains open, as our counterexamples lie (sharply) in the corresponding Lebesgue spaces.
$\mathcal H_i$ remains open, as our counterexamples lie (sharply) in the corresponding Lebesgue spaces.
We would like to express our gratitude towards the anonymous referee for their helpful remarks that helped improve the exposition.
2. Boundedness of the multilinear spherical maximal function
Let ![]() $m\in {\mathbb N}$ be the index of multilinearity, and t > 0. Define for Schwartz functions
$m\in {\mathbb N}$ be the index of multilinearity, and t > 0. Define for Schwartz functions ![]() $f_1,\dots,f_m$ on the real line:
$f_1,\dots,f_m$ on the real line:
 \begin{equation*}
S^m_t(f_1,\dots,f_m)(x) = \int_{\mathbb{S}^{m-1}} \prod_{i=1}^m f_i(x-ty_i) d\sigma(y),
\end{equation*}
\begin{equation*}
S^m_t(f_1,\dots,f_m)(x) = \int_{\mathbb{S}^{m-1}} \prod_{i=1}^m f_i(x-ty_i) d\sigma(y),
\end{equation*} where ![]() $\mathbb{S}^{m-1}$ is the unit sphere in
$\mathbb{S}^{m-1}$ is the unit sphere in ![]() ${\mathbb R}^{m}$,
${\mathbb R}^{m}$, ![]() $y=(y_1,\dots,y_m)\in \mathbb{S}^{mn-1}$,
$y=(y_1,\dots,y_m)\in \mathbb{S}^{mn-1}$, ![]() $y_i\in{\mathbb R}$ for
$y_i\in{\mathbb R}$ for ![]() $i=1,\dots,m$, and
$i=1,\dots,m$, and ![]() $d\sigma$ is the (normalized) surface measure on
$d\sigma$ is the (normalized) surface measure on ![]() $\mathbb{S}^{m-1}$. The multilinear spherical maximal operator is defined by:
$\mathbb{S}^{m-1}$. The multilinear spherical maximal operator is defined by:
 \begin{equation*}S^m(f_1,\dots,f_m)(x) = \sup_{t \gt 0} S^m_t(|f_1|,\dots,|f_m|)(x) = \sup_{t \gt 0} \int_{\mathbb{S}^{m-1}} \prod_{i=1}^m |f_i(x-ty_i)| d\sigma(y).\end{equation*}
\begin{equation*}S^m(f_1,\dots,f_m)(x) = \sup_{t \gt 0} S^m_t(|f_1|,\dots,|f_m|)(x) = \sup_{t \gt 0} \int_{\mathbb{S}^{m-1}} \prod_{i=1}^m |f_i(x-ty_i)| d\sigma(y).\end{equation*}Proof of Theorem 1, boundedness part
By sublinearity, we can assume without a loss of generality that ![]() $f,g \geq 0$. Fix then two indices
$f,g \geq 0$. Fix then two indices ![]() $p_1,p_2 \gt 2.$
$p_1,p_2 \gt 2.$
Decomposing the integral over ![]() $\mathbb{S}^1$ as the sum of the integrals over eight parts of the circle, we see that it is enough to deal with the integral over the set:
$\mathbb{S}^1$ as the sum of the integrals over eight parts of the circle, we see that it is enough to deal with the integral over the set:
 \begin{equation*}\left\{(y_1,y_2)\in \mathbb{S}^1\,:\, 0\leq y_1 \leq \dfrac1{\sqrt{2}}\leq y_2\leq 1\right\},\end{equation*}
\begin{equation*}\left\{(y_1,y_2)\in \mathbb{S}^1\,:\, 0\leq y_1 \leq \dfrac1{\sqrt{2}}\leq y_2\leq 1\right\},\end{equation*}as the treatment over the other sets is essentially equivalent. We then explicitly parametrize the circle over this arc, to obtain:
 \begin{align*} S^2_{t}(f,g)(x) &= \int_{0}^{1/\sqrt{2}} f(x-ty_1)g(x-t\sqrt{1-y_1^2}) \frac{dy_1}{\sqrt{1-y_1^2}}\\
&\leq \int_{0}^{1/\sqrt{2}} f(x-ty_1)g(x-t\sqrt{1-y_1^2})dy_1\\
&=\int_{0}^{1/\sqrt{2}} f(x-ty_1)y_1^{-\frac{1-\varepsilon}2}g(x-t\sqrt{1-y_1^2}) y_1^{\frac{1-\varepsilon}2}dy_1\\
&\leq \left(\int_{0}^{1/\sqrt{2}} f^2(x-ty_1) y_1^{-1+\varepsilon} dy_1\right)^{1/2}\left( \int_{0}^{1/\sqrt{2}} g^2(x-t\sqrt{1-y_1^2}) y_1^{1-\varepsilon} dy_1 \right)^{1/2},
\end{align*}
\begin{align*} S^2_{t}(f,g)(x) &= \int_{0}^{1/\sqrt{2}} f(x-ty_1)g(x-t\sqrt{1-y_1^2}) \frac{dy_1}{\sqrt{1-y_1^2}}\\
&\leq \int_{0}^{1/\sqrt{2}} f(x-ty_1)g(x-t\sqrt{1-y_1^2})dy_1\\
&=\int_{0}^{1/\sqrt{2}} f(x-ty_1)y_1^{-\frac{1-\varepsilon}2}g(x-t\sqrt{1-y_1^2}) y_1^{\frac{1-\varepsilon}2}dy_1\\
&\leq \left(\int_{0}^{1/\sqrt{2}} f^2(x-ty_1) y_1^{-1+\varepsilon} dy_1\right)^{1/2}\left( \int_{0}^{1/\sqrt{2}} g^2(x-t\sqrt{1-y_1^2}) y_1^{1-\varepsilon} dy_1 \right)^{1/2},
\end{align*} where ɛ > 0 small, to be chosen later. Since  $y^{-1+\varepsilon}\chi_{0\leq y \leq {1/\sqrt{2}}}\in L^1$ and is decreasing for any
$y^{-1+\varepsilon}\chi_{0\leq y \leq {1/\sqrt{2}}}\in L^1$ and is decreasing for any ![]() $\varepsilon \gt 0,$ the maximal function:
$\varepsilon \gt 0,$ the maximal function:
 \begin{equation*}f\mapsto \sup_{t \gt 0} \left(\int_{0}^{1/\sqrt{2}} f^2(x-ty_1) y_1^{-1+\varepsilon} dy_1\right)^{1/2},\end{equation*}
\begin{equation*}f\mapsto \sup_{t \gt 0} \left(\int_{0}^{1/\sqrt{2}} f^2(x-ty_1) y_1^{-1+\varepsilon} dy_1\right)^{1/2},\end{equation*} is bounded on L p 1, since ![]() $p_1 \gt 2$. For the second term, we change variables by setting
$p_1 \gt 2$. For the second term, we change variables by setting  $z=\sqrt{1-y_1^2}$ to get:
$z=\sqrt{1-y_1^2}$ to get:
 \begin{align*} &\left( \int_{0}^{1/\sqrt{2}} g^2(x-t\sqrt{1-y_1^2}) y_1^{1-\varepsilon} dy_1 \right)^{1/2}= \left( \int_{1/\sqrt{2}}^{1} g^2(x-tz) \left(\sqrt{1-z^2}\right)^{-\varepsilon} zdz \right)^{1/2}\\
\leq &\left( \int_{1/\sqrt{2}}^{1} g^2(x-tz) \left(\sqrt{1-z^2}\right)^{-\varepsilon} dz \right)^{1/2}\\
\leq & \left( \int_{1/\sqrt{2}}^{1} g^{2q}(x-tz) dz\right)^{1/2q}\left( \int_{1/\sqrt{2}}^{1} \dfrac1{\sqrt{1-z^2}^{\varepsilon q'} }dz \right)^{1/2q'},
\end{align*}
\begin{align*} &\left( \int_{0}^{1/\sqrt{2}} g^2(x-t\sqrt{1-y_1^2}) y_1^{1-\varepsilon} dy_1 \right)^{1/2}= \left( \int_{1/\sqrt{2}}^{1} g^2(x-tz) \left(\sqrt{1-z^2}\right)^{-\varepsilon} zdz \right)^{1/2}\\
\leq &\left( \int_{1/\sqrt{2}}^{1} g^2(x-tz) \left(\sqrt{1-z^2}\right)^{-\varepsilon} dz \right)^{1/2}\\
\leq & \left( \int_{1/\sqrt{2}}^{1} g^{2q}(x-tz) dz\right)^{1/2q}\left( \int_{1/\sqrt{2}}^{1} \dfrac1{\sqrt{1-z^2}^{\varepsilon q'} }dz \right)^{1/2q'},
\end{align*} for any ![]() $1\leq q,q'\leq \infty$ with
$1\leq q,q'\leq \infty$ with  $\frac{1}{q}+\frac1{q'}=1$. We choose q sufficiently close to 1 so that
$\frac{1}{q}+\frac1{q'}=1$. We choose q sufficiently close to 1 so that ![]() $2 \lt 2q \lt p_2$ and then we choose ɛ to be sufficiently small so that
$2 \lt 2q \lt p_2$ and then we choose ɛ to be sufficiently small so that ![]() $\varepsilon q' \lt 2$. In this way the second term in the above product is finite, and the maximal function:
$\varepsilon q' \lt 2$. In this way the second term in the above product is finite, and the maximal function:
 \begin{equation*}g\mapsto \sup_{t \gt 0} \left( \int_{1/\sqrt{2}}^{1} g^{2q}(x-tz) dz\right)^{1/2q},\end{equation*}
\begin{equation*}g\mapsto \sup_{t \gt 0} \left( \int_{1/\sqrt{2}}^{1} g^{2q}(x-tz) dz\right)^{1/2q},\end{equation*}is bounded on L p 2. Finally, taking supremum over t > 0 on both sides, we have:
 \begin{align*} &S^2(f,g)(x) \\
&\lesssim \left(\sup_{t \gt 0} \left(\int_{0}^{1/\sqrt{2}} f^2(x-ty_1) y_1^{-1+\varepsilon} dy_1\right)^{1/2}\right) \left(\sup_{t \gt 0}\left( \int_{1/\sqrt{2}}^{1} g^{2q}(x-tz) dz\right)^{1/2q}\right).
\end{align*}
\begin{align*} &S^2(f,g)(x) \\
&\lesssim \left(\sup_{t \gt 0} \left(\int_{0}^{1/\sqrt{2}} f^2(x-ty_1) y_1^{-1+\varepsilon} dy_1\right)^{1/2}\right) \left(\sup_{t \gt 0}\left( \int_{1/\sqrt{2}}^{1} g^{2q}(x-tz) dz\right)^{1/2q}\right).
\end{align*}Taking Lp norms on both sides and using Hölder’s inequality and the bounds discussed above completes the proof of Equation (3).
Before moving on to the proof of the boundedness part of Theorem 2, we remark that the approach adopted below of using the Kolmogorov–Seliverstov–Plessner linearization and complex interpolation is by no means the only possible one; indeed, it has been brought to our attention by the anonymous referee that the results by Grafakos and Kalton in [Reference Grafakos and Kalton19] may also be used to prove that part of Theorem 2.
Proof of Theorem 2, boundedness part
Again, by sublinearity, it is enough to assume that ![]() $f_i\geq 0$ for all
$f_i\geq 0$ for all ![]() $i=1,\dots,m$. For
$i=1,\dots,m$. For ![]() $i_1,i_2\in \{1,\dots,m\}$ we define the half-open tubes (see Figure 3):
$i_1,i_2\in \{1,\dots,m\}$ we define the half-open tubes (see Figure 3):
 \begin{equation*} T_{i_1,i_2} := \left\{(y_1,\dots,y_m)\in[0,1]^m\,: y_{i_1},y_{i_2} \lt \frac12 \right\}.
\end{equation*}
\begin{equation*} T_{i_1,i_2} := \left\{(y_1,\dots,y_m)\in[0,1]^m\,: y_{i_1},y_{i_2} \lt \frac12 \right\}.
\end{equation*}
Figure 3. The tubes ![]() $T_{1,2}$,
$T_{1,2}$, ![]() $T_{2,3}$ and
$T_{2,3}$ and ![]() $T_{1,3}$.
$T_{1,3}$.
The pointwise bound in Equation (4)
 \begin{equation*}
\sup_{t \gt 0} \left| S^m_t(f_1,\dots,f_m)(x) \right| \lesssim S^2(f_{i_1},f_{i_2})(x) \prod_{j\neq i_1,i_2} M(f_j)(x),
\end{equation*}
\begin{equation*}
\sup_{t \gt 0} \left| S^m_t(f_1,\dots,f_m)(x) \right| \lesssim S^2(f_{i_1},f_{i_2})(x) \prod_{j\neq i_1,i_2} M(f_j)(x),
\end{equation*}along with Theorem 1, the well-known bounds for the Hardy–Littlewood maximal function, and Hölder’s inequality yield strong-type bounds (5) for all:
 \begin{equation*}\left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)\in \Big(T_{i_1,i_2}\setminus\{0,1\}^m\Big) \bigcup\{(0,\dots,0)\},\end{equation*}
\begin{equation*}\left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)\in \Big(T_{i_1,i_2}\setminus\{0,1\}^m\Big) \bigcup\{(0,\dots,0)\},\end{equation*}and weak-type bounds (6) for
 \begin{equation*}\left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)\in \big(\{0,1\}^m\setminus\{(0,\dots,0)\}\big) \bigcap T_{i_1,i_2}.
\end{equation*}
\begin{equation*}\left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)\in \big(\{0,1\}^m\setminus\{(0,\dots,0)\}\big) \bigcap T_{i_1,i_2}.
\end{equation*} We graph the tubes ![]() $T_{{i_1},{i_2}}$ in Figure 3 for m = 3. The multilinear Riesz–Thorin theorem [Reference Grafakos17, Corollary 7.2.11] states that, for a multilinear operator, strong-type bounds (5) on two points in
$T_{{i_1},{i_2}}$ in Figure 3 for m = 3. The multilinear Riesz–Thorin theorem [Reference Grafakos17, Corollary 7.2.11] states that, for a multilinear operator, strong-type bounds (5) on two points in ![]() $[0,1]^m$ yield strong-type bounds on the line segment connecting them. The operator Sm is not linear, but we can use the Kolmogorov–Seliverstov–Plessner linearization (cf. [Reference Zygmund32, Chapter XIII]): Let
$[0,1]^m$ yield strong-type bounds on the line segment connecting them. The operator Sm is not linear, but we can use the Kolmogorov–Seliverstov–Plessner linearization (cf. [Reference Zygmund32, Chapter XIII]): Let ![]() $\tau:{\mathbb R}\to (0,\infty)$ be a measurable function and define:
$\tau:{\mathbb R}\to (0,\infty)$ be a measurable function and define:
 \begin{equation*} S^m_{\tau} (f_1,\dots,f_m) (x) :=\int_{\mathbb S^{m-1}} \prod_{j=1}^{m} f_j(x-\tau(x) y^j) d\sigma_{m-1}(y^1,\dots,y^m).
\end{equation*}
\begin{equation*} S^m_{\tau} (f_1,\dots,f_m) (x) :=\int_{\mathbb S^{m-1}} \prod_{j=1}^{m} f_j(x-\tau(x) y^j) d\sigma_{m-1}(y^1,\dots,y^m).
\end{equation*} If ![]() $S^m_{\tau}$ is uniformly bounded from
$S^m_{\tau}$ is uniformly bounded from ![]() $L^{p_1}\times\cdots\times L^{p_m}$ to Lp for all such measurable functions τ, then Sm is bounded on the same space. For any given measurable function τ, the operator
$L^{p_1}\times\cdots\times L^{p_m}$ to Lp for all such measurable functions τ, then Sm is bounded on the same space. For any given measurable function τ, the operator ![]() $S^m_{\tau}$ is linear and we can thus use complex interpolation from the bounds on the
$S^m_{\tau}$ is linear and we can thus use complex interpolation from the bounds on the ![]() $T_{{i_1},{i_2}}$’s. Since these bounds do not depend on τ, we also obtain them for Sm. Therefore, we conclude that Sm is strong-type bounded (5) for all
$T_{{i_1},{i_2}}$’s. Since these bounds do not depend on τ, we also obtain them for Sm. Therefore, we conclude that Sm is strong-type bounded (5) for all  $\left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)$ that satisfy the conditions (a)–(c) in the statement of the theorem, which are precisely the points in the convex hull of
$\left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)$ that satisfy the conditions (a)–(c) in the statement of the theorem, which are precisely the points in the convex hull of
 \begin{equation*}\bigcup_{i_1,i_2} \Big( T_{i_1,i_2} \setminus\{0,1\}^m\Big) \bigcup\{(0,\dots,0)\}.\end{equation*}
\begin{equation*}\bigcup_{i_1,i_2} \Big( T_{i_1,i_2} \setminus\{0,1\}^m\Big) \bigcup\{(0,\dots,0)\}.\end{equation*} To confirm this, let  $\frac{1}{\vec{p}} = \left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)\in [0,1]^m$ be in the set of exponents such that (a), (b), and (c) are satisfied. If there at least 2 indices i 1,i 2 such that
$\frac{1}{\vec{p}} = \left(\frac{1}{p_1},\dots,\frac{1}{p_m}\right)\in [0,1]^m$ be in the set of exponents such that (a), (b), and (c) are satisfied. If there at least 2 indices i 1,i 2 such that ![]() $p_{i_1},p_{i_2} \gt 2$ then
$p_{i_1},p_{i_2} \gt 2$ then ![]() $\frac{1}{\vec{p}}$ belongs in the tube
$\frac{1}{\vec{p}}$ belongs in the tube ![]() $T_{i_1,i_2}$. If
$T_{i_1,i_2}$. If ![]() $p_i\leq2$ for all
$p_i\leq2$ for all ![]() $i=1,\dots,m$, then the critical condition is (a) and
$i=1,\dots,m$, then the critical condition is (a) and ![]() $\frac{1}{\vec{p}} $ belongs to the convex hull of
$\frac{1}{\vec{p}} $ belongs to the convex hull of ![]() $\mathcal H \cup \{0\}$. We interpolate the bounds on the tubes
$\mathcal H \cup \{0\}$. We interpolate the bounds on the tubes ![]() $T_{i_1,i_2}$ to obtain strong-type bounds on the convex hull of
$T_{i_1,i_2}$ to obtain strong-type bounds on the convex hull of ![]() $\mathcal H \cup \{0\}$, except for
$\mathcal H \cup \{0\}$, except for ![]() $\mathcal{H}$ itself. Similarly, if
$\mathcal{H}$ itself. Similarly, if ![]() $p_i \gt 2$ and
$p_i \gt 2$ and ![]() $p_j\leq 2$ for all j ≠ i, then the critical condition is:
$p_j\leq 2$ for all j ≠ i, then the critical condition is:
 \begin{equation*}\sum_{j\neq i} \frac1{p_j} \lt m-\frac32,\end{equation*}
\begin{equation*}\sum_{j\neq i} \frac1{p_j} \lt m-\frac32,\end{equation*} one of the conditions in (b). Then ![]() $\frac{1}{\vec{p}} $ belongs in the convex hull of
$\frac{1}{\vec{p}} $ belongs in the convex hull of ![]() $\mathcal{H}_i\cup \{te_i, t \in (0,1/2)\}$ and interpolation between points in
$\mathcal{H}_i\cup \{te_i, t \in (0,1/2)\}$ and interpolation between points in
 \begin{equation*}\bigcup_{j\neq i} T_{i,j}\end{equation*}
\begin{equation*}\bigcup_{j\neq i} T_{i,j}\end{equation*} yields strong-type bounds on this region minus ![]() $\mathcal{H}_i$ itself.
$\mathcal{H}_i$ itself.
3. Counterexamples
Our starting point is Stein’s counterexample for the (sub)linear spherical maximal function in [Reference Stein30], which is the function  $f(x)=|x|^{-n/p}\left(-\log(|x|)\right)^{-\frac{1+\varepsilon}{p}}\chi_{|x| \lt 1/2}(x)$ for some ɛ > 0. Then
$f(x)=|x|^{-n/p}\left(-\log(|x|)\right)^{-\frac{1+\varepsilon}{p}}\chi_{|x| \lt 1/2}(x)$ for some ɛ > 0. Then ![]() $f\in L^p({\mathbb R}^n)$, while
$f\in L^p({\mathbb R}^n)$, while ![]() $Sf \in L^p({\mathbb R}^n)$ if and only if
$Sf \in L^p({\mathbb R}^n)$ if and only if ![]() $p \gt \frac{n}{n-1}$.
$p \gt \frac{n}{n-1}$.
For the bilinear case the authors in [Reference Grafakos, He and Honzík18] use the same functions along with a geometric argument to ensure that in the diagonal ![]() $(y,y)\in {\mathbb R}^{2n}$,
$(y,y)\in {\mathbb R}^{2n}$, ![]() $y\in {\mathbb R}^n$, of the sphere
$y\in {\mathbb R}^n$, of the sphere ![]() $\mathbb{S}^{2n-1}$ the integral in the definition of
$\mathbb{S}^{2n-1}$ the integral in the definition of ![]() $S^2(f_1,f_2)(x)$ is large enough to provide a counterexample. This was further expanded to the multilinear case in [Reference Dosidis12].
$S^2(f_1,f_2)(x)$ is large enough to provide a counterexample. This was further expanded to the multilinear case in [Reference Dosidis12].
This counterexample is not optimal in one dimension, as was shown in [Reference Heo, Hong and Yang21], and a Knapp-type example further restricts the boundedness range from p > 1 (which the example in [Reference Grafakos, He and Honzík18] implies) to ![]() $p_1,p_2\geq 2$. Here we improve the example in [Reference Heo, Hong and Yang21], by introducing a blow-up function as in [Reference Stein30] in order to tackle the boundedness in the end-point cases
$p_1,p_2\geq 2$. Here we improve the example in [Reference Heo, Hong and Yang21], by introducing a blow-up function as in [Reference Stein30] in order to tackle the boundedness in the end-point cases ![]() $p_1=2$ and
$p_1=2$ and ![]() $p_2=2$.
$p_2=2$.
Proof of Theorem 1, counterexample part
In [Reference Heo, Hong and Yang21] the authors showed that if the strong type bound Equation (3) holds, then ![]() $p_1,p_2\geq 2$. Moreover, in [Reference Barrionuevo, Grafakos, He, Honzík and Oliveira4] it was shown that
$p_1,p_2\geq 2$. Moreover, in [Reference Barrionuevo, Grafakos, He, Honzík and Oliveira4] it was shown that  $p=\frac{p_1p_2}{p_1+p_2} \gt 1$. A combination of the two examples shows that
$p=\frac{p_1p_2}{p_1+p_2} \gt 1$. A combination of the two examples shows that ![]() $p_1,p_2 \gt 2$ necessarily holds even for the weak type bound. We thus focus on this latter observation.
$p_1,p_2 \gt 2$ necessarily holds even for the weak type bound. We thus focus on this latter observation.
Let ![]() $g=\chi_{[-10,10]}$ and
$g=\chi_{[-10,10]}$ and  $f(x)=|x|^{-1/2}\left(-\log(|x|)\right)^{-1}\chi_{[-1/2,1/2]}(x)$. Then
$f(x)=|x|^{-1/2}\left(-\log(|x|)\right)^{-1}\chi_{[-1/2,1/2]}(x)$. Then ![]() $f\in L^2({\mathbb R})$ and
$f\in L^2({\mathbb R})$ and ![]() $g\in L^{p_2}({\mathbb R})$ for any
$g\in L^{p_2}({\mathbb R})$ for any ![]() $p_2\geq 1$. For any
$p_2\geq 1$. For any ![]() $1/4\leq x\leq 1/2$ we choose t = x in the definition of
$1/4\leq x\leq 1/2$ we choose t = x in the definition of ![]() $S^2(f,g)$ to estimate it from below by:
$S^2(f,g)$ to estimate it from below by:
 \begin{align*} S^2(f,g) (x) \geq& \int_{0}^{1} |x-xy|^{-1/2}\left(-\log(|x-xy|)\right)^{-1} \frac{dy}{\sqrt{1-y^2}}\\
&\geq \frac{\sqrt{x}}{\sqrt{2}} \int_{0}^{1}(x-xy)^{-1} \left(-\log(x-xy)\right)^{-1}dy\\
&\geq \frac{1}{\sqrt{2x}} \int_{0}^{x} u^{-1} \left(-\log(u)\right)^{-1}du=+\infty,
\end{align*}
\begin{align*} S^2(f,g) (x) \geq& \int_{0}^{1} |x-xy|^{-1/2}\left(-\log(|x-xy|)\right)^{-1} \frac{dy}{\sqrt{1-y^2}}\\
&\geq \frac{\sqrt{x}}{\sqrt{2}} \int_{0}^{1}(x-xy)^{-1} \left(-\log(x-xy)\right)^{-1}dy\\
&\geq \frac{1}{\sqrt{2x}} \int_{0}^{x} u^{-1} \left(-\log(u)\right)^{-1}du=+\infty,
\end{align*} where we changed variables ![]() $u = x - xy$ in the passage from the second to the third line. Therefore
$u = x - xy$ in the passage from the second to the third line. Therefore ![]() $S^2(f,g) (x) = +\infty$ on a set of positive measure and the result follows for the
$S^2(f,g) (x) = +\infty$ on a set of positive measure and the result follows for the ![]() $p_1 =2$ case. Since the case
$p_1 =2$ case. Since the case ![]() $p_2=2$ is symmetric, this finishes our proof.
$p_2=2$ is symmetric, this finishes our proof.
For the multilinear function we have two critical boundary cases: ![]() $\mathcal{H}$ and
$\mathcal{H}$ and ![]() $\mathcal{H}_i$, since all of the
$\mathcal{H}_i$, since all of the ![]() $\mathcal{H}_i$’s are similar by the symmetry of the operator. In the first case the counterexample is a characteristic function at the origin, similar to the functions in [Reference Dosidis12, Reference Grafakos, He and Honzík18, Reference Stein30]. For the
$\mathcal{H}_i$’s are similar by the symmetry of the operator. In the first case the counterexample is a characteristic function at the origin, similar to the functions in [Reference Dosidis12, Reference Grafakos, He and Honzík18, Reference Stein30]. For the ![]() $\mathcal{H}_i$’s we use a Knapp-type example similar to the one in [Reference Heo, Hong and Yang21], a tube at the origin tangent to the sphere along the ith axis.
$\mathcal{H}_i$’s we use a Knapp-type example similar to the one in [Reference Heo, Hong and Yang21], a tube at the origin tangent to the sphere along the ith axis.
For the benefit of the reader, we first show that the open set of exponents is optimal. In this case characteristic functions suffice, which simplifies the computations and showcases the relevant geometry of the examples. We then include the appropriate blow-up in order to exclude strong-type bounds on ![]() $\mathcal{H}$ and
$\mathcal{H}$ and ![]() $\mathcal{H}_i$,
$\mathcal{H}_i$, ![]() $i=1,\dots,m$.
$i=1,\dots,m$.
Proof of Theorem 2, counterexample part
We start by showing that the open set of exponents in Theorem 2 is optimal.
Necessity of condition (a): If ![]() $f_1=\cdots=f_m= \chi_{[-\delta,\delta]}$, then for
$f_1=\cdots=f_m= \chi_{[-\delta,\delta]}$, then for ![]() $1/2\leq x\leq 1$ and
$1/2\leq x\leq 1$ and ![]() $t=x\sqrt{m}$, we have:
$t=x\sqrt{m}$, we have:
 \begin{align*}
S^m(f_1,\dots,f_m) & \ge \int_{\mathbb{S}^{m-1}} \prod_{i=1}^m \chi_{[-\delta,\delta]}(x(1-\sqrt{m}y_j)) d\sigma(y_1,\dots,y_m) \cr
& \ge \int_{\mathbb{S}^{m-1}} \prod_{j=1}^m \chi_{[-\frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}, \frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}]}(y_j) d\sigma(y_1,\dots,y_m) \cr
& \gt rsim \int \prod_{j=1}^m \chi_{[-\frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}, \frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}]}(y_j) d y_1 \dots dy_{m-1} \gt rsim \delta^{m-1},
\end{align*}
\begin{align*}
S^m(f_1,\dots,f_m) & \ge \int_{\mathbb{S}^{m-1}} \prod_{i=1}^m \chi_{[-\delta,\delta]}(x(1-\sqrt{m}y_j)) d\sigma(y_1,\dots,y_m) \cr
& \ge \int_{\mathbb{S}^{m-1}} \prod_{j=1}^m \chi_{[-\frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}, \frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}]}(y_j) d\sigma(y_1,\dots,y_m) \cr
& \gt rsim \int \prod_{j=1}^m \chi_{[-\frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}, \frac{\delta}{x\sqrt{m}} - \frac{1}{\sqrt{m}}]}(y_j) d y_1 \dots dy_{m-1} \gt rsim \delta^{m-1},
\end{align*} and thus, if Sm is bounded from ![]() $L^{p_1} \times \cdots \times L^{p_m} \to L^p,$ we should have
$L^{p_1} \times \cdots \times L^{p_m} \to L^p,$ we should have
 \begin{equation*}\delta^{m-1}\lesssim \|S^m(f_1,\dots,f_m)\|_{L^p}\lesssim \prod_{i=1}^m \|f_i\|_{L^{p_i}} \leq \delta^{\sum_{i=1}^m \frac{1}{p_i}},\end{equation*}
\begin{equation*}\delta^{m-1}\lesssim \|S^m(f_1,\dots,f_m)\|_{L^p}\lesssim \prod_{i=1}^m \|f_i\|_{L^{p_i}} \leq \delta^{\sum_{i=1}^m \frac{1}{p_i}},\end{equation*} and therefore  $\sum\limits_{i=1}^m \frac{1}{p_i} \leq m - 1$.
$\sum\limits_{i=1}^m \frac{1}{p_i} \leq m - 1$.
Necessity of condition (b): We set ![]() $f_1=\chi_{[-10\sqrt{m},10\sqrt{m}]}$ and
$f_1=\chi_{[-10\sqrt{m},10\sqrt{m}]}$ and ![]() $f_2=\cdots=f_m=\chi_{[-\delta,\delta]}$. For
$f_2=\cdots=f_m=\chi_{[-\delta,\delta]}$. For ![]() $1/2\leq x\leq 1$ we choose
$1/2\leq x\leq 1$ we choose ![]() $t=x\sqrt{m-1}$ to estimate Sm from below. Analogously to the previous case, we have then:
$t=x\sqrt{m-1}$ to estimate Sm from below. Analogously to the previous case, we have then:
 \begin{align*}
S^m(f_1,\dots,f_m) & \ge \int_{\mathbb{S}^{m-1}} \chi_{[-10\sqrt{m},10\sqrt{m}]}(y_1) \prod_{j=2}^{m} \chi_{[-\delta,\delta]}(x(1-\sqrt{m-1}y_j)) d\sigma(y_1,\dots,y_m) \cr
& \ge \int_{\mathbb{S}^{m-1}} \prod_{j=2}^m \chi_{[-\frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}, \frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}]}(y_j) d\sigma(y_1,\dots,y_m) \cr
& \gt rsim \int_{|y_1| \le \sqrt{2\delta/x}} \left( \int \prod_{j=2}^m \chi_{[-\frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}, \frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}]}(y_j)\right.\\ & \qquad \left. d y_2 \dots dy_{m-1} \right) \, dy_1 \cr
& \gt rsim \delta^{m-3/2}.
\end{align*}
\begin{align*}
S^m(f_1,\dots,f_m) & \ge \int_{\mathbb{S}^{m-1}} \chi_{[-10\sqrt{m},10\sqrt{m}]}(y_1) \prod_{j=2}^{m} \chi_{[-\delta,\delta]}(x(1-\sqrt{m-1}y_j)) d\sigma(y_1,\dots,y_m) \cr
& \ge \int_{\mathbb{S}^{m-1}} \prod_{j=2}^m \chi_{[-\frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}, \frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}]}(y_j) d\sigma(y_1,\dots,y_m) \cr
& \gt rsim \int_{|y_1| \le \sqrt{2\delta/x}} \left( \int \prod_{j=2}^m \chi_{[-\frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}, \frac{\delta}{x\sqrt{m-1}} - \frac{1}{\sqrt{m-1}}]}(y_j)\right.\\ & \qquad \left. d y_2 \dots dy_{m-1} \right) \, dy_1 \cr
& \gt rsim \delta^{m-3/2}.
\end{align*} Thus, if Sm is bounded from ![]() $L^{p_1} \times \cdots \times L^{p_m} \to L^p,$
$L^{p_1} \times \cdots \times L^{p_m} \to L^p,$
 \begin{equation*}\delta^{m-\frac32}\lesssim \|S^m(f_1,\dots,f_m)\|_{L^p}\lesssim \prod_{i=1}^m \|f_i\|_{L^{p_i}} \lesssim_m \delta^{\sum_{i=2}^m \frac{1}{p_i}},\end{equation*}
\begin{equation*}\delta^{m-\frac32}\lesssim \|S^m(f_1,\dots,f_m)\|_{L^p}\lesssim \prod_{i=1}^m \|f_i\|_{L^{p_i}} \lesssim_m \delta^{\sum_{i=2}^m \frac{1}{p_i}},\end{equation*} and therefore  $\sum\limits_{i=2}^m \frac{1}{p_i} \leq m - \frac{3}{2}$.
$\sum\limits_{i=2}^m \frac{1}{p_i} \leq m - \frac{3}{2}$.
We have thus showed that, in order for strong-type bounds to hold in Theorem 2, the set of exponents needs to be in the closure of the set defined by (a)–(c) in the statement of that result. With that proved, we move on to proving that the strong-type bounds fail also on the boundary sets ![]() $\mathcal{H}$ and
$\mathcal{H}$ and ![]() $\mathcal{H}_i, i=1,\dots,m.$
$\mathcal{H}_i, i=1,\dots,m.$
First of all, we note the following calculus fact, which was also used in [Reference Grafakos, He and Honzík18].
Lemma 1. Let ![]() $r_1,r_2 \gt 0$,
$r_1,r_2 \gt 0$,  $t,s \lt e^{-\frac{r_2}{r_1}}$ and
$t,s \lt e^{-\frac{r_2}{r_1}}$ and ![]() $t\leq C s$ for some
$t\leq C s$ for some ![]() $C\geq 1$. Then, there exists an absolute constant C ʹ (depending only on
$C\geq 1$. Then, there exists an absolute constant C ʹ (depending only on ![]() $C,$
$C,$ ![]() $r_1,$ r 2) such that:
$r_1,$ r 2) such that:
 \begin{equation}
s^{-r_1}\left(\log \frac{1}{s}\right)^{-r_2}\leq C' t^{-r_1}\left(\log \frac{1}{t}\right)^{-r_2}.
\end{equation}
\begin{equation}
s^{-r_1}\left(\log \frac{1}{s}\right)^{-r_2}\leq C' t^{-r_1}\left(\log \frac{1}{t}\right)^{-r_2}.
\end{equation} We then let  $f_i= |x|^{-1/p_i}\left(-\log|x|\right)^{-2/p_i}\chi_{[-1/2,1/2]}$ for
$f_i= |x|^{-1/p_i}\left(-\log|x|\right)^{-2/p_i}\chi_{[-1/2,1/2]}$ for ![]() $i=1,\dots,m$, and note that
$i=1,\dots,m$, and note that ![]() $f_i\in L^{p_i}({\mathbb R})$. For large x > 0, we choose
$f_i\in L^{p_i}({\mathbb R})$. For large x > 0, we choose ![]() $t=x\sqrt{m}$ to estimate
$t=x\sqrt{m}$ to estimate  $S^m(\vec{f})(x)$ from below by focusing on the region:
$S^m(\vec{f})(x)$ from below by focusing on the region:
 \begin{equation*}V_m(x):= \left\{(y_1,\dots,y_m)\in \mathbb{S}^{m-1} \, : \, \left|\frac1{\sqrt{m}} - y_1\right|, \cdots, \left|\frac1{\sqrt{m}} - y_{m-1}\right| \lt \frac1{300 m \cdot x\sqrt{m}}\right\}. \end{equation*}
\begin{equation*}V_m(x):= \left\{(y_1,\dots,y_m)\in \mathbb{S}^{m-1} \, : \, \left|\frac1{\sqrt{m}} - y_1\right|, \cdots, \left|\frac1{\sqrt{m}} - y_{m-1}\right| \lt \frac1{300 m \cdot x\sqrt{m}}\right\}. \end{equation*}This yields the lower bound:
 \begin{align*} S^m(f_1,\dots,f_m) (x) &\geq \int_{V_m(x)} \prod_{i=1}^m f_i(x-\sqrt{m}xy_i)d\sigma(\vec{y})\\
&\geq \int_{V_m(x)}\prod_{i=1}^m|x-\sqrt{m}xy_i|^{-1/p_i}\left(-\log(|x-\sqrt{m}xy_i|)\right)^{-2/p_i}d\sigma(\vec{y}).
\end{align*}
\begin{align*} S^m(f_1,\dots,f_m) (x) &\geq \int_{V_m(x)} \prod_{i=1}^m f_i(x-\sqrt{m}xy_i)d\sigma(\vec{y})\\
&\geq \int_{V_m(x)}\prod_{i=1}^m|x-\sqrt{m}xy_i|^{-1/p_i}\left(-\log(|x-\sqrt{m}xy_i|)\right)^{-2/p_i}d\sigma(\vec{y}).
\end{align*} Notice now that, for ![]() $\vec{y} \in V^{+}_m(x) = \{\vec{y}\in V_m(x)\, :\, y_m \gt 0 \},$ we have,
$\vec{y} \in V^{+}_m(x) = \{\vec{y}\in V_m(x)\, :\, y_m \gt 0 \},$ we have,
 \begin{align*}
\left| \frac{1}{\sqrt{m}} - y_m \right| & = \frac{1}{|\frac1{\sqrt{m}} + y_m|} \left|\frac{1}{m} - y_m^2 \right| \leq \sqrt{m} \left| \frac{1}{m} - \left(1-\sum_{j \le {m-1}} y_j^2 \right) \right| \cr
& \leq 3 \sum_{j \le m-1} \left| y_j - \frac{1}{\sqrt{m}}\right| \lt 3(m-1) \frac{1}{300 m \cdot x\sqrt{m}} \lt \frac{1}{100 x \sqrt{m}}.
\end{align*}
\begin{align*}
\left| \frac{1}{\sqrt{m}} - y_m \right| & = \frac{1}{|\frac1{\sqrt{m}} + y_m|} \left|\frac{1}{m} - y_m^2 \right| \leq \sqrt{m} \left| \frac{1}{m} - \left(1-\sum_{j \le {m-1}} y_j^2 \right) \right| \cr
& \leq 3 \sum_{j \le m-1} \left| y_j - \frac{1}{\sqrt{m}}\right| \lt 3(m-1) \frac{1}{300 m \cdot x\sqrt{m}} \lt \frac{1}{100 x \sqrt{m}}.
\end{align*} This in turn implies that the new variables ![]() $u_i := x - x\sqrt{m} y_i, i=1,\dots,m,$ satisfy
$u_i := x - x\sqrt{m} y_i, i=1,\dots,m,$ satisfy  $(\sum_{i\le m-1} |u_i|^2)^{1/2}, |u_m| \lt e^{-2}$, which allows us to use Lemma 1 since
$(\sum_{i\le m-1} |u_i|^2)^{1/2}, |u_m| \lt e^{-2}$, which allows us to use Lemma 1 since  $\max_{i,j} \frac{p_i}{p_j} = 2$ for indices in
$\max_{i,j} \frac{p_i}{p_j} = 2$ for indices in ![]() $\mathcal H$.
$\mathcal H$.
With this in mind, we locally parametrize ![]() $V^{+}_m(x)$ in terms of the first
$V^{+}_m(x)$ in terms of the first ![]() $(m-1)$ coordinates and use the aforementioned change of variables
$(m-1)$ coordinates and use the aforementioned change of variables ![]() $\vec{y} \mapsto \tilde{u}$ in the lower bound above, noticing we are in a position to use Lemma 1, between
$\vec{y} \mapsto \tilde{u}$ in the lower bound above, noticing we are in a position to use Lemma 1, between ![]() $|u_i|$ and
$|u_i|$ and ![]() $|\tilde{u}|,$ where
$|\tilde{u}|,$ where ![]() $\tilde{u} := (u_1,\dots,u_{m-1}).$ This implies, thus,
$\tilde{u} := (u_1,\dots,u_{m-1}).$ This implies, thus,
 \begin{align*}
S^m(f_1,\dots,f_m) (x) & \ge C_m |x|^{1-m} \int_{B^{m-1}(0,\frac1{300m})} |\tilde{u}|^{-\frac1p} \left(-\log(|\tilde{u}|)\right)^{-\frac{2}{p}}d\tilde{u}\\
& \gt rsim \begin{cases} |x|^{1-m} & \text{if } \frac1p = m-1,\\
\infty & \text{if } \frac1p \gt m-1. \end{cases}
\end{align*}
\begin{align*}
S^m(f_1,\dots,f_m) (x) & \ge C_m |x|^{1-m} \int_{B^{m-1}(0,\frac1{300m})} |\tilde{u}|^{-\frac1p} \left(-\log(|\tilde{u}|)\right)^{-\frac{2}{p}}d\tilde{u}\\
& \gt rsim \begin{cases} |x|^{1-m} & \text{if } \frac1p = m-1,\\
\infty & \text{if } \frac1p \gt m-1. \end{cases}
\end{align*} This deals with the lack of strong-type bounds for the set ![]() $\mathcal{H}$.
$\mathcal{H}$.
We deal with the lack of strong-type bounds in each ![]() $\mathcal{H}_i$ in a similar manner. Without loss of generality we focus on
$\mathcal{H}_i$ in a similar manner. Without loss of generality we focus on ![]() $\mathcal{H}_m.$ Let then
$\mathcal{H}_m.$ Let then  $f_i= |x|^{-1/p_i}\left(-\log|x|\right)^{-2/p_i}\chi_{[-1/2,1/2]}$ for
$f_i= |x|^{-1/p_i}\left(-\log|x|\right)^{-2/p_i}\chi_{[-1/2,1/2]}$ for ![]() $i=1,\dots,m-1,$ and
$i=1,\dots,m-1,$ and  $f_m = |x|^{-1/p_m} \left( \log |x|\right)^{-2/p_m} \chi_{{\mathbb R} \setminus [-2,2]}.$ Note that
$f_m = |x|^{-1/p_m} \left( \log |x|\right)^{-2/p_m} \chi_{{\mathbb R} \setminus [-2,2]}.$ Note that ![]() $f_i\in L^{p_i}({\mathbb R})$. For large x > 0, we choose
$f_i\in L^{p_i}({\mathbb R})$. For large x > 0, we choose ![]() $t=x\sqrt{m-1}$ to estimate
$t=x\sqrt{m-1}$ to estimate  $S^m(\vec{f})(x)$ from below by focusing on the region:
$S^m(\vec{f})(x)$ from below by focusing on the region:
 \begin{equation*}W_m(x):= \left\{\vec{y}\in \mathbb{S}^{m-1} \, : \, \left|\frac1{\sqrt{m-1}} - y_1\right|,\cdots, \left|\frac1{\sqrt{m-1}} - y_{m-1}\right| \lt \frac{10^{-4}}{m x\sqrt{m-1}}\right\}, \end{equation*}
\begin{equation*}W_m(x):= \left\{\vec{y}\in \mathbb{S}^{m-1} \, : \, \left|\frac1{\sqrt{m-1}} - y_1\right|,\cdots, \left|\frac1{\sqrt{m-1}} - y_{m-1}\right| \lt \frac{10^{-4}}{m x\sqrt{m-1}}\right\}, \end{equation*} over which ![]() $|1-y_m\sqrt{m-1}| \approx 1$. Moreover, it can be seen that - by similar methods to the ones employed in the analysis of
$|1-y_m\sqrt{m-1}| \approx 1$. Moreover, it can be seen that - by similar methods to the ones employed in the analysis of ![]() $V_m(x)$ above - for
$V_m(x)$ above - for ![]() $\vec{y} \in W_m(x),$ we have
$\vec{y} \in W_m(x),$ we have  $\left( 1 - \sum_{i \le m-1} y_i^2 \right)^{-1/2} \ge c_m \left( \frac{x}{|\tilde{v}|} \right)^{1/2}, $ where
$\left( 1 - \sum_{i \le m-1} y_i^2 \right)^{-1/2} \ge c_m \left( \frac{x}{|\tilde{v}|} \right)^{1/2}, $ where ![]() $c_m \gt 0$ is a constant depending only on
$c_m \gt 0$ is a constant depending only on ![]() $m,$ and
$m,$ and ![]() $\tilde{v} = (v_1,\dots,v_{m-1}),$ where
$\tilde{v} = (v_1,\dots,v_{m-1}),$ where ![]() $v_i = x - x \sqrt{m-1}y_i.$ Parametrizing locally in terms of the first
$v_i = x - x \sqrt{m-1}y_i.$ Parametrizing locally in terms of the first ![]() $(m-1)$ coordinates, changing variables
$(m-1)$ coordinates, changing variables ![]() $\vec{y} \mapsto \tilde{v}$ and using Lemma 1 again, we obtain:
$\vec{y} \mapsto \tilde{v}$ and using Lemma 1 again, we obtain:
 \begin{align*} S^m & (f_1,\dots,f_m) (x) \geq \int_{W_m(x)} \prod_{i=1}^{m} f_i(x-\sqrt{m-1}xy_i)d\sigma(\vec{y})\\ \gt rsim & x^{\frac32-m -\frac1{p_m}} \left(\log x\right)^{-\frac2{p_m}}\int_{B^{m-1}(0,\frac{10^{-4}}{m})} |\tilde{v}|^{- \frac12-\sum\limits_{i=1}^{m-1}\frac1{p_i} } \left(-\log(|\tilde{v}|)\right)^{-\sum\limits_{i=1}^{m-1}\frac2{p_i}}\, d\tilde{v}\\ \gt rsim & \begin{cases} x^{-\frac1p} \left(\log x\right)^{-\frac2{p_m}} & \text{if } \sum\limits_{i\leq m-1}\frac1{p_i} = m-\frac32,\\
\infty & \text{if } \sum\limits_{i\leq m-1}\frac1{p_i} \gt m-\frac32. \end{cases}
\end{align*}
\begin{align*} S^m & (f_1,\dots,f_m) (x) \geq \int_{W_m(x)} \prod_{i=1}^{m} f_i(x-\sqrt{m-1}xy_i)d\sigma(\vec{y})\\ \gt rsim & x^{\frac32-m -\frac1{p_m}} \left(\log x\right)^{-\frac2{p_m}}\int_{B^{m-1}(0,\frac{10^{-4}}{m})} |\tilde{v}|^{- \frac12-\sum\limits_{i=1}^{m-1}\frac1{p_i} } \left(-\log(|\tilde{v}|)\right)^{-\sum\limits_{i=1}^{m-1}\frac2{p_i}}\, d\tilde{v}\\ \gt rsim & \begin{cases} x^{-\frac1p} \left(\log x\right)^{-\frac2{p_m}} & \text{if } \sum\limits_{i\leq m-1}\frac1{p_i} = m-\frac32,\\
\infty & \text{if } \sum\limits_{i\leq m-1}\frac1{p_i} \gt m-\frac32. \end{cases}
\end{align*} Thus, when  $\sum\limits_{i=1}^{m-1}\frac1{p_i} = m-\frac32$, the above calculation shows that
$\sum\limits_{i=1}^{m-1}\frac1{p_i} = m-\frac32$, the above calculation shows that  $S^m(\vec{f})(x) \gt rsim x^{-\frac1p} \left(\log\frac1x\right)^{-\frac2{p_m}}$ for x sufficiently large, and thus
$S^m(\vec{f})(x) \gt rsim x^{-\frac1p} \left(\log\frac1x\right)^{-\frac2{p_m}}$ for x sufficiently large, and thus  $S^m(\vec{f})\not\in L^p$, since
$S^m(\vec{f})\not\in L^p$, since  $\frac{2p}{p_m} \lt 1$. This completes the proof of the fact that no strong-type bounds can hold in the sets
$\frac{2p}{p_m} \lt 1$. This completes the proof of the fact that no strong-type bounds can hold in the sets ![]() $\mathcal{H}_i.$
$\mathcal{H}_i.$
Finally, suppose that (c) is not satisfied. The counterexample in [Reference Dosidis12, Proposition 2] shows that the strong-type bound in Equation (5) cannot hold, since if, for instance, ![]() $p_1=\cdots=p_k=1$ and
$p_1=\cdots=p_k=1$ and ![]() $p_{k+1}=\cdots=p_m=\infty$, we may take
$p_{k+1}=\cdots=p_m=\infty$, we may take ![]() $f_1=\cdots=f_k=\chi_{(-1,1)}$ and
$f_1=\cdots=f_k=\chi_{(-1,1)}$ and ![]() $f_{k+1}=\cdots=f_m \equiv 1$. Then, for large x > 0 and
$f_{k+1}=\cdots=f_m \equiv 1$. Then, for large x > 0 and ![]() $t=x\sqrt{k}$:
$t=x\sqrt{k}$:
 \begin{align*}
S^m(f_1,\dots,f_m)(x) &\geq \int_{B^{k}(0,1)} \prod_{i=1}^k |f_i(x-x\sqrt{k}y_i)| dy_1\dots dy_k\\
& \gt rsim |x|^{-k},
\end{align*}
\begin{align*}
S^m(f_1,\dots,f_m)(x) &\geq \int_{B^{k}(0,1)} \prod_{i=1}^k |f_i(x-x\sqrt{k}y_i)| dy_1\dots dy_k\\
& \gt rsim |x|^{-k},
\end{align*}pointwise, which shows that Equation (5) cannot hold in this case.□
Funding statement
The first author was supported by the Primus research programme PRIMUS/21/SCI/002 of Charles University. The second author was supported by the European Research Council under the Grant Agreement No. 721675 ‘Regularity and Stability in Partial Differential Equations (RSPDE)’.
Competing interests
None declared.