Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T04:53:56.640Z Has data issue: false hasContentIssue false
  • English
  • Français

The Motion of a Flat Plate from Rest in a Visco-elastic Liquid

Published online by Cambridge University Press:  20 January 2009

F. M. Leslie
F. M. Leslie
Affiliation:
Department of Mathematics, King'S College, Newcastle-upon-Tyne 1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Oldroyd (1) considered non-Newtonian liquids for which the stress tensor sik and the rate of strain tensor eik=½(υk,i+υi,k)are related as follows

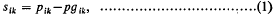
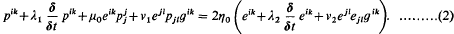
Here υi denotes the velocity vector, p an isotropic pressure, gik the metric tensor, and t time; η0 is a constant having the dimensions of viscosity and λ1, λ2, μ0, ν1, ν2, are constants having the dimension of time. Covariant suffixes are written below, contravariant above and the usual summation convention is employed. A suffix i following a comma indicates covariant differentiation with respect to the space variable xi.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 13 , Issue 3 , June 1963 , pp. 223 - 233
Copyright
Copyright © Edinburgh Mathematical Society 1963

References

REFERENCES

Oldroyd, J. G., P.R.S.A., 245 (1958), 278.Google Scholar
Oldroyd, J. G., P.R.S.A., 200 (1950), 523.Google Scholar
Leslie, F. M., Q.J.M.A.M., 14 (1961), 36.Google Scholar
Oldroyd, J. G., Q.J.M.A.M., 4 (1951), 271.Google Scholar
Toms, B. A. and Strawbridge, D. J., Trans. Farad. Soc., 49 (1953), 1225.CrossRefGoogle Scholar