Article contents
More on automorphism groups of laminated near-rings
Published online by Cambridge University Press: 20 January 2009
Extract
We will assume throughout this paper that polynomials are nonconstant. Let P be any complex polynomial and let 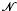 p denote the near-ring of all continuous selfmaps of the complex plane where addition of functions is pointwise and multiplication is defined by fg = f ο P ο g for all f,g∈
p denote the near-ring of all continuous selfmaps of the complex plane where addition of functions is pointwise and multiplication is defined by fg = f ο P ο g for all f,g∈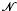 p. The near-ring
p. The near-ring 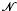 p is referred to as a laminated near-ring and P is referred to as the laminating element or laminator. In [1] the problem was posed of determining Aut
p is referred to as a laminated near-ring and P is referred to as the laminating element or laminator. In [1] the problem was posed of determining Aut 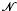 p the automorphism group of
p the automorphism group of 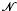 p. It was shown that exactly three infinite groups occur as automorphism groups of the laminated near-rings
p. It was shown that exactly three infinite groups occur as automorphism groups of the laminated near-rings 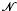 p and for each of the three groups those polynomials P were characterized such that Aut
p and for each of the three groups those polynomials P were characterized such that Aut 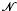 p is isomorphic to that particular group. The infinite groups turn out to be GL(2), the full linear group of all 2×2 nonsingular real matrices and two of its subgroups.
p is isomorphic to that particular group. The infinite groups turn out to be GL(2), the full linear group of all 2×2 nonsingular real matrices and two of its subgroups.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1988
References
REFERENCES
- 2
- Cited by


