The aim of this paper is to develop analytic techniques to deal with the monotonicity of certain combinatorial sequences. On the one hand, a criterion for the monotonicity of the function 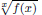is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions

is considered, where ζ(x) and Γ(x) are the Riemann zeta function and the Euler Gamma function, respectively. Consequently, the strict log-concavities of the function θ(x) (a conjecture of Chen et al.) and 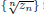for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients are demonstrated. In particular, this contains some results of Chen et al., and Luca and Stănică. Finally, by researching the logarithmically complete monotonicity of some functions, the infinite log-monotonicity of the sequence

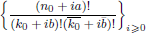
is proved. This generalizes two results of Chen et al. that both the Catalan numbers 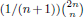and the central binomial coefficients 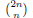are infinitely log-monotonic, and strengthens one result of Su and Wang that is log-convex in n for positive integers d > δ. In addition, the asymptotically infinite log-monotonicity of derangement numbers is showed. In order to research the stronger properties of the above functions θ(x) and F(x), the logarithmically complete monotonicity of functions

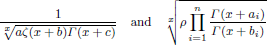
is also obtained, which generalizes the results of Lee and Tepedelenlioǧlu, and Qi and Li.