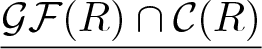1. Introduction
Throughout this paper, R will be an associative ring with identity, and all modules will be, unless otherwise specified, unital left R-modules. When right R-modules need to be used, they will be denoted as MR, while in these cases left R-modules will be denoted by ![]() $_R M$. Whenever it is convenient, right R-modules are identified with modules over the opposite ring
$_R M$. Whenever it is convenient, right R-modules are identified with modules over the opposite ring ![]() $R^\mathrm{op}$. We use
$R^\mathrm{op}$. We use ![]() $\mathcal{I}(R)$,
$\mathcal{I}(R)$, ![]() $\mathcal{P}(R)$,
$\mathcal{P}(R)$, ![]() $\mathcal{F}(R)$ and
$\mathcal{F}(R)$ and ![]() $\mathcal{C}(R)$ to denote the classes of injective, projective, flat and cotorsion R-modules, respectively.
$\mathcal{C}(R)$ to denote the classes of injective, projective, flat and cotorsion R-modules, respectively.
From a theorem by Christensen, Estrada and Thompson [Reference Bravo, Gillespie and Hovey8, Theorem 4.5], the subcategory ![]() $\mathcal{GF}(R)\cap\mathcal{C}(R)$ of Gorenstein flat and cotorsion R-modules is a Frobenius category with projective-injective objects all flat-cotorsion R-modules. Hence, the stable category
$\mathcal{GF}(R)\cap\mathcal{C}(R)$ of Gorenstein flat and cotorsion R-modules is a Frobenius category with projective-injective objects all flat-cotorsion R-modules. Hence, the stable category ![]() $\mathcal{E}_0:=\underline{\mathcal{GF}(R)\cap\mathcal{C}(R)}$ is a triangulated category. On the other hand, Šaroch and
$\mathcal{E}_0:=\underline{\mathcal{GF}(R)\cap\mathcal{C}(R)}$ is a triangulated category. On the other hand, Šaroch and  [Reference Saroch and Stovicek32, Section 4] constructed a hereditary abelian model structure
[Reference Saroch and Stovicek32, Section 4] constructed a hereditary abelian model structure ![]() $\mathcal{M}_0$ where the class of cofibrant objects coincides with
$\mathcal{M}_0$ where the class of cofibrant objects coincides with ![]() $\mathcal{GF}(R)$ and the class of fibrant objects coincides with
$\mathcal{GF}(R)$ and the class of fibrant objects coincides with ![]() $\mathcal{C}(R)$. As a particular case of Estrada, Iacob and Pérez [Reference Estrada, Iacob and Pérez18, Corollary 4.6] (see also [Reference Bennis, El Maaouy, García Rozas and Oyonarte3, Corollary 4.18]), the homotopy category
$\mathcal{C}(R)$. As a particular case of Estrada, Iacob and Pérez [Reference Estrada, Iacob and Pérez18, Corollary 4.6] (see also [Reference Bennis, El Maaouy, García Rozas and Oyonarte3, Corollary 4.18]), the homotopy category ![]() ${\rm Ho}(\mathcal{M}_0)$ of this model structure is triangulated equivalent to the stable category
${\rm Ho}(\mathcal{M}_0)$ of this model structure is triangulated equivalent to the stable category ![]() $\mathcal{E}_0$.
$\mathcal{E}_0$.
In the first part of this paper, § 3, we are interested in a general situation of the same kind of problem: that of modules of bounded Gorenstein flat dimension. It is therefore natural to ask whether we can construct a model structure such that the class of cofibrant objects coincides with the class ![]() $\mathcal{GF}_n(R)$ of all modules having Gorenstein flat dimension at most an integer
$\mathcal{GF}_n(R)$ of all modules having Gorenstein flat dimension at most an integer ![]() $n\geq 0$.
$n\geq 0$.
First, we show that there is a trivial model structure (in the sense that every module is a trivial object)
In fact, this is nothing but saying that ![]() $\mathcal{GF}_n(R)$ is the left hand of a complete cotorsion pair. However, the following result shows more than that.
$\mathcal{GF}_n(R)$ is the left hand of a complete cotorsion pair. However, the following result shows more than that.
Theorem A. (The n-Gorenstein flat cotorsion pair)
The class ![]() $\mathcal{GF}_n(R)$ forms the left hand of a perfect hereditary cotorsion pair
$\mathcal{GF}_n(R)$ forms the left hand of a perfect hereditary cotorsion pair ![]() $(\mathcal{GF}_n(R),\mathcal{GC}_n(R))$ with
$(\mathcal{GF}_n(R),\mathcal{GC}_n(R))$ with ![]() $\mathcal{GC}_n(R)=\mathcal{PGF}(R)^\perp\cap \mathcal{F}_n(R)^\perp$.
$\mathcal{GC}_n(R)=\mathcal{PGF}(R)^\perp\cap \mathcal{F}_n(R)^\perp$.
In particular, ![]() $\mathcal{GF}_n(R)$ is covering and
$\mathcal{GF}_n(R)$ is covering and ![]() $\mathcal{GC}_n(R)$ is enveloping.
$\mathcal{GC}_n(R)$ is enveloping.
Theorem A is essential to obtain our next main result (Theorem 3.6). This result provides us with a (non-trivial) model structure where the class of fibrant objects coincides with ![]() $\mathcal{C}_n(R):=\mathcal{F}_n(R)^\perp$ the right
$\mathcal{C}_n(R):=\mathcal{F}_n(R)^\perp$ the right ![]() ${\rm Ext}$-orthogonal class of all R-modules of flat dimension at most n.
${\rm Ext}$-orthogonal class of all R-modules of flat dimension at most n.
One of the consequences of this model structure is that the stable category ![]() $\mathcal{E}_n=\underline{\mathcal{GF}_n(R)\cap\mathcal{C}_n(R)}$ modulo objects in
$\mathcal{E}_n=\underline{\mathcal{GF}_n(R)\cap\mathcal{C}_n(R)}$ modulo objects in ![]() $\mathcal{F}_n(R)\cap\mathcal{C}_n(R)$ is triangulated (Corollary 3.7). In the case n = 0, Liang and Wang [Reference Liang and Wang29, Theorem 1(a)] have recently shown that this stable category is compactly generated when R is right coherent with finite global Gorenstein projective dimension. It is natural to ask whether this generatedness property is inherited by
$\mathcal{F}_n(R)\cap\mathcal{C}_n(R)$ is triangulated (Corollary 3.7). In the case n = 0, Liang and Wang [Reference Liang and Wang29, Theorem 1(a)] have recently shown that this stable category is compactly generated when R is right coherent with finite global Gorenstein projective dimension. It is natural to ask whether this generatedness property is inherited by ![]() $\mathcal{E}_n$ for all
$\mathcal{E}_n$ for all ![]() $n\geq 0$. Based on their work, we answer this question in the positive, assuming only that R has finite global Gorenstein AC-projective dimension.
$n\geq 0$. Based on their work, we answer this question in the positive, assuming only that R has finite global Gorenstein AC-projective dimension.
Theorem B. (The n-Gorenstein flat model structure)
There exists a hereditary abelian model structure on R-Mod
 \begin{equation*}\mathcal{M}_n=\left(\mathcal{GF}_n(R),\mathcal{PGF}(R)^\perp, \mathcal{C}_n(R)\right).\end{equation*}
\begin{equation*}\mathcal{M}_n=\left(\mathcal{GF}_n(R),\mathcal{PGF}(R)^\perp, \mathcal{C}_n(R)\right).\end{equation*}Consequently, there are triangulated equivalences
Furthermore, if R has finite global Gorenstein AC-projective dimension, then these triangulated categories are compactly generated.
The n-Gorenstein flat model structure has been found for two particular rings: (Iwanaga-)Gorenstein rings by Pérez [Reference Pérez30, Theorem 14.3.1] where the trivial objects are known and coincide with modules having finite flat dimension and right coherent rings by Xu [Reference Xu35, Theorem 4.5(2)] where less information is known about the class of trivial objects.
Therefore, Theorem B generalizes and improves their results in the sense that we do not need any assumption on the ring R with an explicit description of the trivial objects. This makes Theorem B of interest since the class of trivial objects is the most important class in any model structure for it determines the corresponding homotopy category, as explained in the fundamental theorem of model categories [Reference Hovey23, Theorem 1.2.10].
We point out that the proof of Theorem B is different from that of Pérez and Xu. It is mainly based on the work developed by Šaroch and  in [Reference Saroch and Stovicek32]. One of the key results (Theorem 3.4) is a new and useful characterization of modules having finite Gorenstein flat dimension.
in [Reference Saroch and Stovicek32]. One of the key results (Theorem 3.4) is a new and useful characterization of modules having finite Gorenstein flat dimension.
A guiding principle in the development of Gorenstein homological algebra is to study analogues of results concerning absolute homological dimensions. For example, consider the well-known questions: (Q1) Is every Gorenstein projective module Gorenstein flat? and (Q2) Is the class of Gorenstein projective modules special precovering? These questions have been studied by many authors, such as Cortés-Izurdiaga and Šaroch [Reference Cortés-Izurdiaga and Saroch10], Emmanouil [Reference Emmanouil14], Enochs and Jenda [Reference Enochs and Jenda15] and Iacob [Reference Iacob28] among others. One could also ask similar questions in the case of Ding projective modules. However, all these questions remain open.
Šaroch and  [Reference Saroch and Stovicek32], on the other hand, introduced PGF modules and showed that they are Gorenstein flat and they form a special precovering class. These properties can be seen as positive answers to Questions (Q1) and (Q2) if we think of PGF modules as an alternative definition of Gorenstein projective modules.
[Reference Saroch and Stovicek32], on the other hand, introduced PGF modules and showed that they are Gorenstein flat and they form a special precovering class. These properties can be seen as positive answers to Questions (Q1) and (Q2) if we think of PGF modules as an alternative definition of Gorenstein projective modules.
Our main purpose of § 4 is to support the following claim: ‘the PGF dimension could serve as an alternative definition of the Gorenstein (Ding) projective dimension over any ring’.
Recall [Reference Enochs, Jenda and López-Ramos16, Definition 2.1] that a ring R is left n-perfect if every flat R-module has projective dimension ![]() $\leq n$. In particular, left perfect rings are exactly left 0-perfect rings. We show (Theorem 4.2) that a ring R is left n-perfect if and only if every Gorenstein flat left R-module has PGF dimension at most n. In the case n = 0, we obtain other equivalent assertions similar to the classical ones, supporting the above claim.
$\leq n$. In particular, left perfect rings are exactly left 0-perfect rings. We show (Theorem 4.2) that a ring R is left n-perfect if and only if every Gorenstein flat left R-module has PGF dimension at most n. In the case n = 0, we obtain other equivalent assertions similar to the classical ones, supporting the above claim.
It follows by [Reference Saroch and Stovicek32, Theorem 4.4] that any PGF module is Gorenstein projective. But whether the converse is true remains open. This leaves us with another question: (Q3) When is any Gorenstein projective a PGF module? This question was first asked and investigated by Šaroch and  [Reference Saroch and Stovicek32] and later by Iacob [Reference Iacob28]. It turns out that this question is closely related to Questions (Q1) and (Q2) (see Remark 4.13).
[Reference Saroch and Stovicek32] and later by Iacob [Reference Iacob28]. It turns out that this question is closely related to Questions (Q1) and (Q2) (see Remark 4.13).
One nice way to study Question (Q3) is to measure how far a Gorenstein projective module is from being PGF. It is proved (Proposition 4.11) that this can be reduced to two cases: either Gorenstein projective modules are as close as possible to PGF, i.e. Gorenstein projective and PGF modules coincide, or, as far as possible, and this means that the PGF dimension of any Gorenstein projective module is infinite.
Next, we obtain a variety of conditions that are equivalent to the first case (Proposition 4.11). Under these equivalent assertions, we get a positive answer to Questions (Q1) and (Q2) (Corollary 4.13). In particular, this is the case when R is right weak coherent and left n-perfect or R is a ring such that every injective right R-module has finite flat dimension.
Right weak coherent rings were introduced by Izurdiaga in [Reference Cortés-Izurdiaga9] as a natural generalization of right coherent rings. They are rings for which the direct product of any family of flat R-modules has finite flat dimension. It turns out that these rings provide a general framework in which one can replace the assumption of being coherent with that of being weak coherent (see Corollary 4.9 and Remark 4.12).
The rest of § 4 is devoted to the global dimension of R with respect to the class ![]() $\mathcal{PGF}(R)$ and its link to other global dimensions. First, we provide simple ways to compute it (Theorem 4.14). This result is then used to show our last main result of this paper which, along with its consequences (Corollaries 4.17 and 4.19), clearly support our claim above. The following result states that, unlike the classes
$\mathcal{PGF}(R)$ and its link to other global dimensions. First, we provide simple ways to compute it (Theorem 4.14). This result is then used to show our last main result of this paper which, along with its consequences (Corollaries 4.17 and 4.19), clearly support our claim above. The following result states that, unlike the classes ![]() $\mathcal{PGF}(R)$ and
$\mathcal{PGF}(R)$ and ![]() $\mathcal{GP}(R)$, their global dimensions coincide.
$\mathcal{GP}(R)$, their global dimensions coincide.
Theorem C. For any ring R, we have the following equality:
2. Preliminaries
Resolutions. Given a class ![]() $\mathcal{X}$ of R-modules and a class
$\mathcal{X}$ of R-modules and a class ![]() $\mathcal{Y}$ of right R-modules, an
$\mathcal{Y}$ of right R-modules, an ![]() $\mathcal{X}$-resolution of an R-module M is an exact complex
$\mathcal{X}$-resolution of an R-module M is an exact complex ![]() $\cdots\to X_1\to X_0\to M\to 0$ where
$\cdots\to X_1\to X_0\to M\to 0$ where ![]() $X_i\in\mathcal{X}$.
$X_i\in\mathcal{X}$.
A sequence X of R-modules is called ![]() $\left(\mathcal{Y}\otimes_R-\right)$-exact (respectively,
$\left(\mathcal{Y}\otimes_R-\right)$-exact (respectively, ![]() ${\rm Hom}_R(\mathcal{X},-)$-exact,
${\rm Hom}_R(\mathcal{X},-)$-exact, ![]() $ {\rm Hom}_R(-,\mathcal{X})$-exact) if
$ {\rm Hom}_R(-,\mathcal{X})$-exact) if ![]() $Y\otimes_R\textbf{X}$ (respectively,
$Y\otimes_R\textbf{X}$ (respectively, ![]() ${\rm Hom}_R(X,\textbf{X})$,
${\rm Hom}_R(X,\textbf{X})$, ![]() ${\rm Hom}_R(\textbf{X},X)$) is an exact complex for every
${\rm Hom}_R(\textbf{X},X)$) is an exact complex for every ![]() $Y\in\mathcal{Y}$ (respectively,
$Y\in\mathcal{Y}$ (respectively, ![]() $X\in\mathcal{X}$).
$X\in\mathcal{X}$).
An R-module M is said to have ![]() $\mathcal{X}$-resolution dimension at most an integer
$\mathcal{X}$-resolution dimension at most an integer ![]() $n\geq 0$,
$n\geq 0$, ![]() ${\rm resdim}_\mathcal{X}(M)\leq n$, if M has a finite
${\rm resdim}_\mathcal{X}(M)\leq n$, if M has a finite ![]() $\mathcal{X}$-resolution:
$\mathcal{X}$-resolution: ![]() $0\to X_n\to\cdots\to X_1\to X_0\to M\to 0.$ If n is the least non-negative integer for which such a sequence exists then its
$0\to X_n\to\cdots\to X_1\to X_0\to M\to 0.$ If n is the least non-negative integer for which such a sequence exists then its ![]() $\mathcal{X}$-resolution dimension is precisely
$\mathcal{X}$-resolution dimension is precisely ![]() $n,$ and if there is no such n then we define its
$n,$ and if there is no such n then we define its ![]() $\mathcal{X}$-resolution dimension as
$\mathcal{X}$-resolution dimension as ![]() $\infty$.
$\infty$.
Given a class of R-modules ![]() $\mathcal{Z}$, the
$\mathcal{Z}$, the ![]() $\mathcal{X}$-dimension of
$\mathcal{X}$-dimension of ![]() $\mathcal{Z}$ is defined as:
$\mathcal{Z}$ is defined as:
![]() $\mathcal{X}$-coresolutions and
$\mathcal{X}$-coresolutions and ![]() $\mathcal{X}$-coresolution dimensions are defined dually.
$\mathcal{X}$-coresolution dimensions are defined dually.
Gorenstein modules and dimensions. An R-module M is called Gorenstein flat if it is a syzygy of an ![]() $(\mathcal{I}(R^\mathrm{op})\otimes_R-)$-exact exact sequence of flat R-modules. Replacing flat with projective, we get the definition of projectively coresolved Gorenstein flat (PGF for short) modules [Reference Saroch and Stovicek32]. An R-module M is called Gorenstein projective if it is a syzygy of a
$(\mathcal{I}(R^\mathrm{op})\otimes_R-)$-exact exact sequence of flat R-modules. Replacing flat with projective, we get the definition of projectively coresolved Gorenstein flat (PGF for short) modules [Reference Saroch and Stovicek32]. An R-module M is called Gorenstein projective if it is a syzygy of a ![]() ${\rm Hom}_R(-,\mathcal{P}(R))$-exact exact sequence of projective R-modules. Gorenstein injective modules are defined dually. We let
${\rm Hom}_R(-,\mathcal{P}(R))$-exact exact sequence of projective R-modules. Gorenstein injective modules are defined dually. We let ![]() $\mathcal{GF}(R)$ (respectively,
$\mathcal{GF}(R)$ (respectively, ![]() $\mathcal{PGF}(R)$,
$\mathcal{PGF}(R)$, ![]() $\mathcal{GP}(R)$ and
$\mathcal{GP}(R)$ and ![]() $\mathcal{GI}(R)$) denote the subcategory of Gorenstein flat (respectively, PGF, Gorenstein projective and Gorenstein injective) R-modules.
$\mathcal{GI}(R)$) denote the subcategory of Gorenstein flat (respectively, PGF, Gorenstein projective and Gorenstein injective) R-modules.
The Gorenstein flat (respectively, PGF, Gorenstein projective, Gorenstein injective) dimension of an R-module M is defined as ![]() ${\rm Gfd}_R(M):={\rm resdim}_{\mathcal{GF}(R)}(M)$ (respectively,
${\rm Gfd}_R(M):={\rm resdim}_{\mathcal{GF}(R)}(M)$ (respectively, ![]() ${\rm {PGF}\mbox{-}pd}_R(M):={\rm resdim}_{\mathcal{PGF}(R)}(M)$,
${\rm {PGF}\mbox{-}pd}_R(M):={\rm resdim}_{\mathcal{PGF}(R)}(M)$, ![]() ${\rm Gpd}_R(M):={\rm resdim}_{\mathcal{GP}(R)}(M)$ and
${\rm Gpd}_R(M):={\rm resdim}_{\mathcal{GP}(R)}(M)$ and ![]() ${\rm Gid}_R(M):={\rm coresdim}_{\mathcal{GI}(R)}(M)$).
${\rm Gid}_R(M):={\rm coresdim}_{\mathcal{GI}(R)}(M)$).
Let ![]() ${\rm GPD}(R)$ (respectively,
${\rm GPD}(R)$ (respectively, ![]() ${\rm GID}(R)$) denote the global Gorenstein projective (respectively, global Gorenstein injective) dimension of R, i.e.
${\rm GID}(R)$) denote the global Gorenstein projective (respectively, global Gorenstein injective) dimension of R, i.e.
(respectively, ![]() ${\rm GID}(R):={\rm Gid}_R(R\text{-Mod})={\rm sup}\{{\rm Gid}_R(M)|M\in R\text{-Mod}\}$).
${\rm GID}(R):={\rm Gid}_R(R\text{-Mod})={\rm sup}\{{\rm Gid}_R(M)|M\in R\text{-Mod}\}$).
Definition 2.1. Let ![]() $\mathcal{F}_n(R)$ and
$\mathcal{F}_n(R)$ and ![]() $\mathcal{GF}_n(R)$ denote the subcategories of R-modules having flat and Gorenstein flat dimension at most
$\mathcal{GF}_n(R)$ denote the subcategories of R-modules having flat and Gorenstein flat dimension at most ![]() $n\geq 0$. We call modules in these subcategories n-flat and n-Gorenstein flat, respectively.
$n\geq 0$. We call modules in these subcategories n-flat and n-Gorenstein flat, respectively.
An R-module M is said to be n-cotorsion (respectively, n-Gorenstein cotorsion) if ![]() ${\rm Ext}^1_R(N,M)$ for all n-flat (respectively, n-Gorenstein flat) modules N. We use
${\rm Ext}^1_R(N,M)$ for all n-flat (respectively, n-Gorenstein flat) modules N. We use ![]() $\mathcal{C}_n(R)$ and
$\mathcal{C}_n(R)$ and ![]() $\mathcal{GC}_n(R)$ to denote the subcategrories of n-cotorsion and n-Gorenstein cotorsion modules, respectively.
$\mathcal{GC}_n(R)$ to denote the subcategrories of n-cotorsion and n-Gorenstein cotorsion modules, respectively.
Note that 0-flat (respectively, Gorenstein 0-flat, 0-cotorsion, 0-Gorenstein cotorsion) modules coincide with the flat (respectively, Gorenstein flat, cotorsion, Gorenstein cotorsion) modules.
Cotorsion pairs. Given an abelian category ![]() $\mathcal{A}$, and a class of objects
$\mathcal{A}$, and a class of objects ![]() $\mathcal{X}$ in
$\mathcal{X}$ in ![]() $\mathcal{A}$, we use the following standard notation:
$\mathcal{A}$, we use the following standard notation:  $\mathcal{X}^\perp=\{A\in\mathcal{A}|{\rm Ext}^1_\mathcal{A}(X,A)=0,\forall X\in\mathcal{X}\}$ and
$\mathcal{X}^\perp=\{A\in\mathcal{A}|{\rm Ext}^1_\mathcal{A}(X,A)=0,\forall X\in\mathcal{X}\}$ and  $^\perp\mathcal{X}=\{A\in\mathcal{A}|{\rm Ext}^1_\mathcal{A}(A,X)=0,\forall X\in\mathcal{X}\}.$
$^\perp\mathcal{X}=\{A\in\mathcal{A}|{\rm Ext}^1_\mathcal{A}(A,X)=0,\forall X\in\mathcal{X}\}.$
An ![]() $\mathcal{X}$-precover of an object
$\mathcal{X}$-precover of an object ![]() $A\in\mathcal{A}$ is a morphism
$A\in\mathcal{A}$ is a morphism ![]() $f:X\to A$ with
$f:X\to A$ with ![]() $X\in \mathcal{X}$, in such a way that
$X\in \mathcal{X}$, in such a way that ![]() $f_*:{\rm Hom}_\mathcal{A}(X',X)\to {\rm Hom}_\mathcal{A}(X',M)$ is surjective for every
$f_*:{\rm Hom}_\mathcal{A}(X',X)\to {\rm Hom}_\mathcal{A}(X',M)$ is surjective for every ![]() $X'\in \mathcal{X}$. An
$X'\in \mathcal{X}$. An ![]() $\mathcal{X}$-precover is called an
$\mathcal{X}$-precover is called an ![]() $\mathcal{X}$-cover if every endomorphism
$\mathcal{X}$-cover if every endomorphism ![]() $g: X\to X$ such that fg = f is an automorphism of X. If every object has an
$g: X\to X$ such that fg = f is an automorphism of X. If every object has an ![]() $\mathcal{X}$-(pre)cover then the class
$\mathcal{X}$-(pre)cover then the class ![]() $\mathcal{X}$ is said to be (pre)covering. An
$\mathcal{X}$ is said to be (pre)covering. An ![]() $\mathcal{X}$-precover is called special if it is epimorphism and
$\mathcal{X}$-precover is called special if it is epimorphism and ![]() ${\rm Ker} f\in\mathcal{X}^\perp$.
${\rm Ker} f\in\mathcal{X}^\perp$. ![]() $\mathcal{X}$-(special pre)envelopes can be defined dually.
$\mathcal{X}$-(special pre)envelopes can be defined dually.
A pair ![]() $\left(\mathcal{X},\mathcal{Y}\right)$ of classes of objects in
$\left(\mathcal{X},\mathcal{Y}\right)$ of classes of objects in ![]() $\mathcal{A}$ is called a cotorsion pair if
$\mathcal{A}$ is called a cotorsion pair if ![]() $\mathcal{X}^\perp=\mathcal{Y}$ and
$\mathcal{X}^\perp=\mathcal{Y}$ and ![]() $\mathcal{X}=^\perp\mathcal{Y}$. A cotorsion pair
$\mathcal{X}=^\perp\mathcal{Y}$. A cotorsion pair ![]() $\left(\mathcal{X},\mathcal{Y}\right)$ is said to be:
$\left(\mathcal{X},\mathcal{Y}\right)$ is said to be:
• Hereditary if
 ${\rm Ext}^i_\mathcal{A}(X,Y)=0$ for every
${\rm Ext}^i_\mathcal{A}(X,Y)=0$ for every  $X\in\mathcal{X}$,
$X\in\mathcal{X}$,  $Y\in\mathcal{Y}$ and
$Y\in\mathcal{Y}$ and  $i\geq 1$.
$i\geq 1$.• Complete if any object in
 $\mathcal{A}$ has a special
$\mathcal{A}$ has a special  $\mathcal{X}$-precover and a special
$\mathcal{X}$-precover and a special  $\mathcal{Y}$-preenvelope.
$\mathcal{Y}$-preenvelope.• Perfect if every module has an
 $\mathcal{X}$-cover and a
$\mathcal{X}$-cover and a  $\mathcal{Y}$-envelope.
$\mathcal{Y}$-envelope.• Cogenerated by a set if there is a set
 $\mathcal{S}$ such that
$\mathcal{S}$ such that  $\mathcal{X}=\mathcal{S}^\perp$.
$\mathcal{X}=\mathcal{S}^\perp$.
It is well-known that a perfect cotorsion pair ![]() $(\mathcal{X},\mathcal{Y})$ in R-Mod is complete. The converse holds when
$(\mathcal{X},\mathcal{Y})$ in R-Mod is complete. The converse holds when ![]() $\mathcal{X}$ is closed under direct limits [Reference Göbel and Trlifaj19, Corollary 2.3.7]. A well-known method for constructing complete cotorsion pairs in R-Mod is to cogenerate one from a set (see [Reference Göbel and Trlifaj19, Theorem 3.2.1], for instance).
$\mathcal{X}$ is closed under direct limits [Reference Göbel and Trlifaj19, Corollary 2.3.7]. A well-known method for constructing complete cotorsion pairs in R-Mod is to cogenerate one from a set (see [Reference Göbel and Trlifaj19, Theorem 3.2.1], for instance).
Abelian model structures. Given a bicomplete category ![]() $\mathcal{A}$, a model structure on
$\mathcal{A}$, a model structure on ![]() $\mathcal{A}$ is given by three classes of morphisms of
$\mathcal{A}$ is given by three classes of morphisms of ![]() $\mathcal{A}$, called cofibrations, fibrations and weak equivalences that satisfy a set of axioms [Reference Hovey23, Definition 1.1.3].
$\mathcal{A}$, called cofibrations, fibrations and weak equivalences that satisfy a set of axioms [Reference Hovey23, Definition 1.1.3].
Over a (bicomplete) abelian category ![]() $\mathcal{A}$, Hovey defined abelian model structures and showed that we can shift all our attention from morphisms to objects [Reference Hovey24, Theorem 2.2]. Namely, an abelian model structure on
$\mathcal{A}$, Hovey defined abelian model structures and showed that we can shift all our attention from morphisms to objects [Reference Hovey24, Theorem 2.2]. Namely, an abelian model structure on ![]() $\mathcal{A}$, is equivalent to a triple (known as Hovey triple)
$\mathcal{A}$, is equivalent to a triple (known as Hovey triple) ![]() $\mathcal{M}=(\mathcal{Q},\mathcal{W},\mathcal{R})$ of classes of objects in
$\mathcal{M}=(\mathcal{Q},\mathcal{W},\mathcal{R})$ of classes of objects in ![]() $\mathcal{A}$ such that
$\mathcal{A}$ such that ![]() $(\mathcal{Q}, \mathcal{W}\cap\mathcal{R})$ and
$(\mathcal{Q}, \mathcal{W}\cap\mathcal{R})$ and ![]() $(\mathcal{Q}\cap\mathcal{W},\mathcal{R})$ are complete cotorsion pairs and
$(\mathcal{Q}\cap\mathcal{W},\mathcal{R})$ are complete cotorsion pairs and ![]() $\mathcal{W}$ is thick. In this case, Q (respectively,
$\mathcal{W}$ is thick. In this case, Q (respectively, ![]() $\mathcal{R}$,
$\mathcal{R}$, ![]() $\mathcal{W}$) is precisely the class of cofibrant (respectively, fibrant, trivial) objects and an abelian model structure (in the sense of [Reference Hovey23, Definition 1.1.3]) is one which the following two conditions are satisfied:
$\mathcal{W}$) is precisely the class of cofibrant (respectively, fibrant, trivial) objects and an abelian model structure (in the sense of [Reference Hovey23, Definition 1.1.3]) is one which the following two conditions are satisfied:
(i) A morphism is a (trivial) cofibration if and only if it is a monomorphism with (trivially) cofibrant cokernel.
(ii) A morphism is a (trivial) fibration if and only if it is an epimorphism with (trivially) fibrant kernel.
An abelian model structure is called hereditary if both of the associated cotorsion pairs are hereditary (see Gillespie [Reference Gillespie22] for a nice survey on hereditary abelian model categories). In this paper, we often identify abelian model structures with Hovey triples.
Given a model structure ![]() $\mathcal{M}$, the homotopy category, denoted as
$\mathcal{M}$, the homotopy category, denoted as ![]() ${\rm Ho}_\mathcal{A}(\mathcal{M})$, is defined by formally inverting the weak equivalences of
${\rm Ho}_\mathcal{A}(\mathcal{M})$, is defined by formally inverting the weak equivalences of ![]() $\mathcal{M}$. More precisely,
$\mathcal{M}$. More precisely, ![]() ${\rm Ho}_\mathcal{A}(\mathcal{M})$ is obtained after localizing
${\rm Ho}_\mathcal{A}(\mathcal{M})$ is obtained after localizing ![]() $\mathcal{A}$ at the class of weak equivalences. If moreover,
$\mathcal{A}$ at the class of weak equivalences. If moreover, ![]() $\mathcal{M}$ is hereditary, the homotopy category is known to be an algebraic triangulated category and it encodes a variety of (relative) homological algebra on
$\mathcal{M}$ is hereditary, the homotopy category is known to be an algebraic triangulated category and it encodes a variety of (relative) homological algebra on ![]() $\mathcal{A}$.
$\mathcal{A}$.
3. n-Gorenstein flat modules and their model structure
In this section, we aim at proving Theorems A and B in the introduction. First, we need some basic properties of n-Gorenstein flat modules.
Proposition 3.1. The class of n-Gorenstein flat R-modules is projectively resolving, closed under direct sums, direct summands and direct limits.
Proof. It is clear that any projective module is Gorenstein flat, and then n-Gorenstein flat. On the other hand, taking W = R in [Reference Bennis, El Maaouy, García Rozas and Oyonarte2], we get that ![]() $\mathcal{GF}(R)={\rm G_WF}(R)$ and this class is closed under extensions by [Reference Saroch and Stovicek32, Theorem 4.11]. Therefore, the class
$\mathcal{GF}(R)={\rm G_WF}(R)$ and this class is closed under extensions by [Reference Saroch and Stovicek32, Theorem 4.11]. Therefore, the class ![]() $\mathcal{GF}_n(R)$ is closed under extensions and kernels of epimorphisms by [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.9] and direct sums and summands by [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Corollary 7.8(2)]. It remains to show that
$\mathcal{GF}_n(R)$ is closed under extensions and kernels of epimorphisms by [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.9] and direct sums and summands by [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Corollary 7.8(2)]. It remains to show that ![]() $\mathcal{GF}_n(R)$ is closed under direct limits.
$\mathcal{GF}_n(R)$ is closed under direct limits.
Following [Reference Adámek and Rosický1, Corollary 1.7 and the Remark that follows it] it suffices to show that the class ![]() $\mathcal{GF}_n(R)$ is closed under well-ordered continuous direct limits of n-Gorenstein flat R-modules:
$\mathcal{GF}_n(R)$ is closed under well-ordered continuous direct limits of n-Gorenstein flat R-modules:
Here continuous (or smooth in the sense of [Reference Adámek and Rosický1]) means that for each limit ordinal ![]() $\beta \lt \lambda$,
$\beta \lt \lambda$,  $M_\beta=\varinjlim_{\alpha \lt \beta} M_\alpha$.
$M_\beta=\varinjlim_{\alpha \lt \beta} M_\alpha$.
• If
 $\lambda \lt \omega$, then
$\lambda \lt \omega$, then  $\lim_{\alpha \lt \lambda} M_\alpha=M_{\lambda-1}\in \mathcal{GF}_n(R)$.
$\lim_{\alpha \lt \lambda} M_\alpha=M_{\lambda-1}\in \mathcal{GF}_n(R)$.• Assume now that
 $\lambda=\omega$. By [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.11], there exists an exact sequence
$\lambda=\omega$. By [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.11], there exists an exact sequence  $0\to M_0\to F_0\to G_0\to 0$ with
$0\to M_0\to F_0\to G_0\to 0$ with  $F_0\in\mathcal{F}_n(R)$ and G 0 Gorenstein flat. Consider the push out
$F_0\in\mathcal{F}_n(R)$ and G 0 Gorenstein flat. Consider the push out
Since ![]() $M_1\in\mathcal{GF}_n(R)$ and G 0 is Gorenstein flat,
$M_1\in\mathcal{GF}_n(R)$ and G 0 is Gorenstein flat, ![]() $V\in\mathcal{GF}_n(R)$. Using again [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.11], we get an exact sequence
$V\in\mathcal{GF}_n(R)$. Using again [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.11], we get an exact sequence ![]() $0\to V\to F_1\to G\to 0$ with
$0\to V\to F_1\to G\to 0$ with ![]() $F_1\in\mathcal{F}_n(R)$ and G Gorenstein flat.
$F_1\in\mathcal{F}_n(R)$ and G Gorenstein flat.
Consider another push out

Since G 0 and G are Gorenstein flat, so is G 1. Therefore, we get the following morphism of exact sequences induced by the morphism ![]() $M_0\to M_1$:
$M_0\to M_1$:

Repeating this process, we get a commutative diagram with exact rows

where ![]() $F_i\in\mathcal{F}_n$ and Gi is Gorenstein flat for every
$F_i\in\mathcal{F}_n$ and Gi is Gorenstein flat for every ![]() $i\geq 0$. Applying the exact functor
$i\geq 0$. Applying the exact functor  $\varinjlim$ to this commutative diagram, we get the induced exact sequence
$\varinjlim$ to this commutative diagram, we get the induced exact sequence
 \begin{equation*}\varinjlim A_m=: 0\to \varinjlim M_m\to \varinjlim F_m\to \varinjlim G_m\to 0\end{equation*}
\begin{equation*}\varinjlim A_m=: 0\to \varinjlim M_m\to \varinjlim F_m\to \varinjlim G_m\to 0\end{equation*} with  $\varinjlim G_m\in \mathcal{GF}(R)\subseteq \mathcal{GF}_n(R)$ by [Reference Yang and Liu36,
Lemma 3.1] and
$\varinjlim G_m\in \mathcal{GF}(R)\subseteq \mathcal{GF}_n(R)$ by [Reference Yang and Liu36,
Lemma 3.1] and  $\varinjlim F_m\in \mathcal{F}_n(R)$ since the functor
$\varinjlim F_m\in \mathcal{F}_n(R)$ since the functor  ${\rm Tor}^R_{n+1}(X,-)$ commutes with direct limits for any right R-module X. Hence,
${\rm Tor}^R_{n+1}(X,-)$ commutes with direct limits for any right R-module X. Hence,  $M_\omega=\varinjlim M_m\in\mathcal{GF}_n(R)$.
$M_\omega=\varinjlim M_m\in\mathcal{GF}_n(R)$.
Finally, using transfinite induction, it is clear that the above argument generalizes and we get that  $\varinjlim_{\alpha \lt \lambda} M_\alpha\in\mathcal{GF}_n(R)$ as desired.
$\varinjlim_{\alpha \lt \lambda} M_\alpha\in\mathcal{GF}_n(R)$ as desired.
The following two lemmas will be used in several places in this paper.
Lemma 3.2. The inclusion ![]() $\mathcal{F}_n(R) \subseteq \mathcal{PGF}(R)^\perp$ holds true.
$\mathcal{F}_n(R) \subseteq \mathcal{PGF}(R)^\perp$ holds true.
Proof. It follows from the fact that ![]() $ \mathcal{PGF}(R)^\perp$ is thick by [Reference Saroch and Stovicek32, Theorem 4.9] and
$ \mathcal{PGF}(R)^\perp$ is thick by [Reference Saroch and Stovicek32, Theorem 4.9] and ![]() $\mathcal{F}(R)\subseteq \mathcal{PGF}(R)^\perp$ by [Reference Saroch and Stovicek32, Theorem 4.11].
$\mathcal{F}(R)\subseteq \mathcal{PGF}(R)^\perp$ by [Reference Saroch and Stovicek32, Theorem 4.11].
Lemma 3.3. ![]() $(\mathcal{F}_n(R),\mathcal{C}_n(R))$ is a perfect and hereditary cotorsion pair cogenerated by a set.
$(\mathcal{F}_n(R),\mathcal{C}_n(R))$ is a perfect and hereditary cotorsion pair cogenerated by a set.
Proof. Follows by [Reference Ding and Mao13, Theorem 3.4(2)] and its proof.
The following characterization of n-Gorenstein flat modules is a key result to show many results in this section. The case n = 0 is due to Šaroch and  [Reference Saroch and Stovicek32, Theorem 4.11].
[Reference Saroch and Stovicek32, Theorem 4.11].
Theorem 3.4. The following assertions are equivalent for any R-module M.
(1) M is n-Gorenstein flat.
(2) There exists a
 ${\rm Hom}_R(-,\mathcal{F}_n(R)\cap\mathcal{C}_n(R))$-exact exact sequence
${\rm Hom}_R(-,\mathcal{F}_n(R)\cap\mathcal{C}_n(R))$-exact exact sequence
 \begin{equation*}0\to K\to L\to M\to 0\end{equation*}
\begin{equation*}0\to K\to L\to M\to 0\end{equation*}where
 $K\in \mathcal{F}_n(R)$ and
$K\in \mathcal{F}_n(R)$ and  $L\in \mathcal{PGF}(R)$.
$L\in \mathcal{PGF}(R)$.(3)
 ${\rm Ext}^1_R(M,C)=0$ for every
${\rm Ext}^1_R(M,C)=0$ for every  $C\in \mathcal{PGF}(R)^\perp\cap \mathcal{C}_n(R)$.
$C\in \mathcal{PGF}(R)^\perp\cap \mathcal{C}_n(R)$.(4) There exists an exact sequence of R-modules
 \begin{equation*}0\to M\to F\to N\to 0\end{equation*}
\begin{equation*}0\to M\to F\to N\to 0\end{equation*}where
 $F\in\mathcal{F}_n(R)$ and
$F\in\mathcal{F}_n(R)$ and  $N\in \mathcal{PGF}(R)$.
$N\in \mathcal{PGF}(R)$.
Consequently, ![]() $\mathcal{F}_n(R)=\mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^\perp$.
$\mathcal{F}_n(R)=\mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^\perp$.
Proof. ![]() $4.\Rightarrow 1.$ It follows by Proposition 3.1 since
$4.\Rightarrow 1.$ It follows by Proposition 3.1 since ![]() $F\in\mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)$ and
$F\in\mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)$ and ![]() $N\in \mathcal{PGF}(R)\subseteq \mathcal{GF}_n(R)$.
$N\in \mathcal{PGF}(R)\subseteq \mathcal{GF}_n(R)$.
![]() $1.\Rightarrow 4.$ Assume that
$1.\Rightarrow 4.$ Assume that ![]() ${\rm Gfd}_R(M)\leq n$ and proceed by induction on n.
${\rm Gfd}_R(M)\leq n$ and proceed by induction on n.
The case n = 0 follows from [Reference Saroch and Stovicek32, Theorem 4.11(4)].
Assume that ![]() $n\geq 1$. There exists an exact sequence
$n\geq 1$. There exists an exact sequence ![]() $0\rightarrow G_n\rightarrow\cdots\rightarrow G_0\rightarrow M\rightarrow 0$, where
$0\rightarrow G_n\rightarrow\cdots\rightarrow G_0\rightarrow M\rightarrow 0$, where ![]() $G_i\in \mathcal{GF}(R)$ for every
$G_i\in \mathcal{GF}(R)$ for every ![]() $i=0,\ldots,n.$ Let
$i=0,\ldots,n.$ Let ![]() $K={\rm Ker}(G_0\to M)$. Clearly,
$K={\rm Ker}(G_0\to M)$. Clearly, ![]() ${\rm Gfd}_R(K)\leq n-1$. So, by induction there exists an exact sequence
${\rm Gfd}_R(K)\leq n-1$. So, by induction there exists an exact sequence ![]() $0\rightarrow K\rightarrow F'\rightarrow N'\rightarrow 0,$ where
$0\rightarrow K\rightarrow F'\rightarrow N'\rightarrow 0,$ where ![]() $N'\in \mathcal{PGF}(R)$ and
$N'\in \mathcal{PGF}(R)$ and ![]() ${\rm fd}_R(F')\leq n-1$. Consider the pushout diagram
${\rm fd}_R(F')\leq n-1$. Consider the pushout diagram

By the middle column D is Gorenstein flat. Using induction again, we get a short exact sequence of R-modules ![]() $0\to D\to F_0\to N\to 0$ where F 0 is flat and
$0\to D\to F_0\to N\to 0$ where F 0 is flat and ![]() $N\in\mathcal{PGF}(R)$.
$N\in\mathcal{PGF}(R)$.
Consider now another pushout diagram

It remains to see that ![]() ${\rm fd}_R(F)\leq n$. But this is true by the middle row since F 0 is flat and
${\rm fd}_R(F)\leq n$. But this is true by the middle row since F 0 is flat and ![]() ${\rm fd}_R(F')\leq n-1$.
${\rm fd}_R(F')\leq n-1$.
![]() $1.\Rightarrow 2.$ The case n = 0 holds by [Reference Saroch and Stovicek32, Theorem 4.11(2)]. So, we may assume that
$1.\Rightarrow 2.$ The case n = 0 holds by [Reference Saroch and Stovicek32, Theorem 4.11(2)]. So, we may assume that ![]() $n\geq 1$. By [Reference Saroch and Stovicek32, Theorem 4.9], there exists a special PGF precover
$n\geq 1$. By [Reference Saroch and Stovicek32, Theorem 4.9], there exists a special PGF precover ![]() $0\to N\to G\to M\to 0.$ By [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.9],
$0\to N\to G\to M\to 0.$ By [Reference Bennis, El Maaouy, García Rozas and Oyonarte2, Proposition 7.9], ![]() ${\rm Gfd}_R(N)\leq {\rm sup}\{{\rm Gfd}_R(G),{\rm Gfd}_R(M)-1\}\leq n-1$ which implies by (4) that there exists an exact sequence of R-modules
${\rm Gfd}_R(N)\leq {\rm sup}\{{\rm Gfd}_R(G),{\rm Gfd}_R(M)-1\}\leq n-1$ which implies by (4) that there exists an exact sequence of R-modules ![]() $0\to N\to K\to G'\to 0$ where
$0\to N\to K\to G'\to 0$ where ![]() ${\rm fd}_R(K)\leq n-1$ and
${\rm fd}_R(K)\leq n-1$ and ![]() $G'\in\mathcal{PGF}(R)$. Consider the pushout
$G'\in\mathcal{PGF}(R)$. Consider the pushout

Since ![]() $\mathcal{PGF}(R)$ is closed under extensions,
$\mathcal{PGF}(R)$ is closed under extensions, ![]() $L\in\mathcal{PGF}(R)$. Then, there exits (by definition) an exact sequence
$L\in\mathcal{PGF}(R)$. Then, there exits (by definition) an exact sequence ![]() $0\to L\to P\to L'\to 0$, with P projective and
$0\to L\to P\to L'\to 0$, with P projective and ![]() $L'\in
\mathcal{PGF}(R)$. Consider now another pushout
$L'\in
\mathcal{PGF}(R)$. Consider now another pushout

Since ![]() ${\rm fd}_R(K)\leq n-1$ and P is projective (then flat),
${\rm fd}_R(K)\leq n-1$ and P is projective (then flat), ![]() $H\in\mathcal{F}_n(R)$ by the middle row. It follows from the following commutative diagram with exact rows
$H\in\mathcal{F}_n(R)$ by the middle row. It follows from the following commutative diagram with exact rows

that ![]() $0\to L\to K\to M\to 0$ is
$0\to L\to K\to M\to 0$ is ![]() ${\rm Hom}_R(-,X)$-exact for any module
${\rm Hom}_R(-,X)$-exact for any module ![]() $X\in\mathcal{F}_n(R)\cap\mathcal{C}_n(R)$.
$X\in\mathcal{F}_n(R)\cap\mathcal{C}_n(R)$.
![]() $ 2.\Rightarrow 3.$ Similar to [Reference Saroch and Stovicek32, Theorem 4.11(2)
$ 2.\Rightarrow 3.$ Similar to [Reference Saroch and Stovicek32, Theorem 4.11(2)![]() $\Rightarrow$(3)], using the fact that any module
$\Rightarrow$(3)], using the fact that any module ![]() $C\in \mathcal{PGF}(R)^\perp\cap \mathcal{C}_n(R)$ has a special n-flat precover which exists by Lemma 3.3.
$C\in \mathcal{PGF}(R)^\perp\cap \mathcal{C}_n(R)$ has a special n-flat precover which exists by Lemma 3.3.
![]() $ 3.\Rightarrow 4.$ Similar to [Reference Saroch and Stovicek32, Theorem 4.11(3)
$ 3.\Rightarrow 4.$ Similar to [Reference Saroch and Stovicek32, Theorem 4.11(3)![]() $\Rightarrow$(4)] using the fact that every module
$\Rightarrow$(4)] using the fact that every module ![]() $F\in \mathcal{PGF}(R)^\perp$ has a special n-flat precover which exists by Lemma 3.3 and that
$F\in \mathcal{PGF}(R)^\perp$ has a special n-flat precover which exists by Lemma 3.3 and that ![]() $\mathcal{F}_n(R)\subseteq \mathcal{PGF}(R)^\perp$ by Lemma 3.2.
$\mathcal{F}_n(R)\subseteq \mathcal{PGF}(R)^\perp$ by Lemma 3.2.
Finally, it remains to show the equality. The inclusion ![]() $\mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)$ is clear and by Lemma 3.2 we also have
$\mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)$ is clear and by Lemma 3.2 we also have ![]() $\mathcal{F}_n(R)\subseteq \mathcal{PGF}(R)^\perp$. Then,
$\mathcal{F}_n(R)\subseteq \mathcal{PGF}(R)^\perp$. Then, ![]() $\mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$. Conversely, if
$\mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$. Conversely, if ![]() $M\in\mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$, then there exists by (4) a split exact sequence of R-modules
$M\in\mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$, then there exists by (4) a split exact sequence of R-modules ![]() $0\to M\to F\to N\to 0$, where
$0\to M\to F\to N\to 0$, where ![]() $N\in\mathcal{PGF}(R)$ and
$N\in\mathcal{PGF}(R)$ and ![]() ${\rm fd}_R(X)\leq n$. Then,
${\rm fd}_R(X)\leq n$. Then, ![]() $M\in \mathcal{F}_n(R)$.
$M\in \mathcal{F}_n(R)$.
The following result, which is Theorem A from the introduction, improves and generalizes [Reference Pérez30, Proposition 14.3.5] and [Reference Xu35, Lemma 4.4]. Here we have a more explicit description of the right hand of the n-Gorenstein flat cotorsion pair without any assumptions on the ring.
Corollary 3.5. The pair ![]() $\left(\mathcal{GF}_n(R),\mathcal{PGF}(R)^\perp\cap \mathcal{C}_n(R)\right)$ is a perfect hereditary cotorsion pair cogenerated by a set.
$\left(\mathcal{GF}_n(R),\mathcal{PGF}(R)^\perp\cap \mathcal{C}_n(R)\right)$ is a perfect hereditary cotorsion pair cogenerated by a set.
Consequently, the following assertions hold.
(a) Every R-module has a n-Gorenstein flat cover and n-Gorenstein cotorsion envelope.
(b) An R-module is n-Gorenstein cotorsion if and only if it is n-cotorsion from
 $\mathcal{PGF}(R)^\perp$.
$\mathcal{PGF}(R)^\perp$.
Proof. Let ![]() $\mathcal{A}=\mathcal{GF}_n(R)$ and
$\mathcal{A}=\mathcal{GF}_n(R)$ and ![]() $\mathcal{B}=\mathcal{PGF}(R)^\perp \cap \mathcal{C}_n(R)$. By Theorem 3.4(3),
$\mathcal{B}=\mathcal{PGF}(R)^\perp \cap \mathcal{C}_n(R)$. By Theorem 3.4(3), ![]() $\mathcal{A}=\;^{\perp}\mathcal{B}$. On the other hand, clearly
$\mathcal{A}=\;^{\perp}\mathcal{B}$. On the other hand, clearly ![]() $\mathcal{PGF}(R)\cup \mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)$. Then,
$\mathcal{PGF}(R)\cup \mathcal{F}_n(R)\subseteq \mathcal{GF}_n(R)$. Then, ![]() $\mathcal{A}^{\perp}=\mathcal{GF}_n(R)^{\perp}\subseteq \mathcal{F}_n(R)^\perp \cap \mathcal{PGF}(R)^\perp=\mathcal{B}$. Hence,
$\mathcal{A}^{\perp}=\mathcal{GF}_n(R)^{\perp}\subseteq \mathcal{F}_n(R)^\perp \cap \mathcal{PGF}(R)^\perp=\mathcal{B}$. Hence, ![]() $\mathcal{A}^{\perp}=\mathcal{B}$ and
$\mathcal{A}^{\perp}=\mathcal{B}$ and ![]() $(\mathcal{A},\mathcal{B})$ is a cotorsion pair.
$(\mathcal{A},\mathcal{B})$ is a cotorsion pair.
Now we prove that this cotorsion pair is perfect. But, since ![]() $\mathcal{GF}_n(R)$ is closed under direct limits by Proposition 3.1(3), we only need to check that it is complete [Reference Göbel and Trlifaj19, Corollary 2.3.7]. Following [Reference Göbel and Trlifaj19, Theorem 3.2.1(b)], a nice way to do that is to show that it is cogenerated by a set. By the proof of [Reference Saroch and Stovicek32, Theorem 4.9],
$\mathcal{GF}_n(R)$ is closed under direct limits by Proposition 3.1(3), we only need to check that it is complete [Reference Göbel and Trlifaj19, Corollary 2.3.7]. Following [Reference Göbel and Trlifaj19, Theorem 3.2.1(b)], a nice way to do that is to show that it is cogenerated by a set. By the proof of [Reference Saroch and Stovicek32, Theorem 4.9], ![]() $(\mathcal{PGF}(R),\mathcal{PGF}(R)^\perp)$ is a cotorsion pair cogenerated by a set
$(\mathcal{PGF}(R),\mathcal{PGF}(R)^\perp)$ is a cotorsion pair cogenerated by a set ![]() $\mathcal{A}_1$. We also know by Lemma 3.3 that the cotorsion pair
$\mathcal{A}_1$. We also know by Lemma 3.3 that the cotorsion pair ![]() $(\mathcal{F}_n(R),\mathcal{C}_n(R))$ is cogenerated by a set
$(\mathcal{F}_n(R),\mathcal{C}_n(R))$ is cogenerated by a set ![]() $\mathcal{A}_2$. Then,
$\mathcal{A}_2$. Then, ![]() $\mathcal{PGF}(R)^\perp \cap \mathcal{C}_n(R)=\mathcal{A}_1^\perp\ \cap\ \mathcal{A}_2^\perp=(\mathcal{A}_1\ \cup\ \mathcal{A}_2)^\perp$. This means that our desired pair is cogenerated by a set and hence complete.
$\mathcal{PGF}(R)^\perp \cap \mathcal{C}_n(R)=\mathcal{A}_1^\perp\ \cap\ \mathcal{A}_2^\perp=(\mathcal{A}_1\ \cup\ \mathcal{A}_2)^\perp$. This means that our desired pair is cogenerated by a set and hence complete.
Now we are ready to prove our second main result in this section. The following result improves [Reference Pérez30, Theorem 14.3.1] and [Reference Xu35, Theorem 4.5] in the sense that we need no extra assumptions on the ring R with an obvious description of the trivial objects.
Theorem 3.6. For any ring R, there exists a hereditary abelian model structure on R-Mod
 \begin{equation*}\mathcal{M}_n:=\left(\mathcal{GF}_n(R),\mathcal{PGF}(R)^\perp, \mathcal{C}_n(R)\right).\end{equation*}
\begin{equation*}\mathcal{M}_n:=\left(\mathcal{GF}_n(R),\mathcal{PGF}(R)^\perp, \mathcal{C}_n(R)\right).\end{equation*} Equivalently, there exists a hereditary abelian model structure on R-Mod, in which the cofibrations coincide with the monomorphisms with n-Gorenstein flat cokernel, the fibrations coincide with the epimorphisms with n-cotorsion kernel, and ![]() $\mathcal{PGF}(R)^\perp$ is the class of trivial objects.
$\mathcal{PGF}(R)^\perp$ is the class of trivial objects.
Proof. By Theorem 3.4, ![]() $\mathcal{F}_n(R)=\mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^\perp$. Then, by Lemma 3.3 and Corollary 3.5, there are two complete and hereditary cotorsion pairs:
$\mathcal{F}_n(R)=\mathcal{GF}_n(R)\cap \mathcal{PGF}(R)^\perp$. Then, by Lemma 3.3 and Corollary 3.5, there are two complete and hereditary cotorsion pairs:
Finally, the class ![]() $\mathcal{PGF}(R)^\perp$ is thick by [Reference Saroch and Stovicek32, Theorem 4.9] which completes the proof.
$\mathcal{PGF}(R)^\perp$ is thick by [Reference Saroch and Stovicek32, Theorem 4.9] which completes the proof.
Recall that a Frobenius category ![]() $\mathcal{A}$ is an exact category with enough injectives and projectives such that the projective objects coincide with the injective objects. In this case, we can form the stable category
$\mathcal{A}$ is an exact category with enough injectives and projectives such that the projective objects coincide with the injective objects. In this case, we can form the stable category ![]() $\underline{\mathcal{A}}:=\mathcal{A}/\sim$, which has the same objects as
$\underline{\mathcal{A}}:=\mathcal{A}/\sim$, which has the same objects as ![]() $\mathcal{A}$ and
$\mathcal{A}$ and ![]() ${\rm Hom}_{\mathcal{A}/\sim}(X,Y):={\rm Hom}_{\mathcal{A}}(X,Y)/\sim$, where
${\rm Hom}_{\mathcal{A}/\sim}(X,Y):={\rm Hom}_{\mathcal{A}}(X,Y)/\sim$, where ![]() $f\sim g$ if and only if f − g factors through a projective-injective object.
$f\sim g$ if and only if f − g factors through a projective-injective object.
The following result can be proved directly as in the case n = 0 (see [Reference Bravo, Gillespie and Hovey8, Theorem 4.5]). However, we follow an alternative approach due to Gillespie [Reference Gillespie21]. Recall [Reference Gillespie21, Sections 4 and 5] that for any hereditary Hovey triple ![]() $\mathcal{M}=(\mathcal{Q},\mathcal{W},\mathcal{R})$, the subcategory
$\mathcal{M}=(\mathcal{Q},\mathcal{W},\mathcal{R})$, the subcategory ![]() $\mathcal{Q}\cap \mathcal{R}$ is a Frobenius exact category (with the exact structure given by the short exact sequences with terms in
$\mathcal{Q}\cap \mathcal{R}$ is a Frobenius exact category (with the exact structure given by the short exact sequences with terms in ![]() $\mathcal{Q}\cap \mathcal{R}$) whose projective-injective objects are precisely those in
$\mathcal{Q}\cap \mathcal{R}$) whose projective-injective objects are precisely those in ![]() $\mathcal{Q}\cap\mathcal{W}\cap\mathcal{R}$. Moreover, the stable category
$\mathcal{Q}\cap\mathcal{W}\cap\mathcal{R}$. Moreover, the stable category ![]() $\underline{\mathcal{Q}\cap\mathcal{R}}$ is triangulated equivalent to
$\underline{\mathcal{Q}\cap\mathcal{R}}$ is triangulated equivalent to ![]() ${\rm Ho}(\mathcal{M})$ (see also [Reference Gillespie22, Proposition 4.2 and Theorem 4.3]). Consequently, we have the following corollary.
${\rm Ho}(\mathcal{M})$ (see also [Reference Gillespie22, Proposition 4.2 and Theorem 4.3]). Consequently, we have the following corollary.
Corollary 3.7. The subcategory ![]() $\mathcal{GF}_n(R)\cap \mathcal{C}_n(R)$ of both n-Gorenstein flat and n-cotorsion R-modules is a Frobenius category. The projective-injective modules are given by objects in
$\mathcal{GF}_n(R)\cap \mathcal{C}_n(R)$ of both n-Gorenstein flat and n-cotorsion R-modules is a Frobenius category. The projective-injective modules are given by objects in ![]() $\mathcal{F}_n(R)\cap\mathcal{C}_n(R)$. Moreover, the homotopy category of the n-Gorenstein flat model structure is triangle equivalent to the stable category
$\mathcal{F}_n(R)\cap\mathcal{C}_n(R)$. Moreover, the homotopy category of the n-Gorenstein flat model structure is triangle equivalent to the stable category ![]() $\underline{\mathcal{GF}_n(R)\cap \mathcal{C}_n(R)}$.
$\underline{\mathcal{GF}_n(R)\cap \mathcal{C}_n(R)}$.
Let ![]() $(\mathcal{T},\Sigma)$ be a triangulated category with coproducts and an autofunctor Σ. Recall that an object C of
$(\mathcal{T},\Sigma)$ be a triangulated category with coproducts and an autofunctor Σ. Recall that an object C of ![]() $\mathcal{T}$ is compact if for each family
$\mathcal{T}$ is compact if for each family ![]() $\{Y_i|i\in I\}$ of objects of
$\{Y_i|i\in I\}$ of objects of ![]() $\mathcal{T}$, the canonical morphism
$\mathcal{T}$, the canonical morphism
 \begin{equation*}\bigoplus_{i\in I} {\rm Hom}_\mathcal{T}(C,Y_i)\to {\rm Hom}_\mathcal{T}(C,\bigoplus_{i\in I}Y_i)\end{equation*}
\begin{equation*}\bigoplus_{i\in I} {\rm Hom}_\mathcal{T}(C,Y_i)\to {\rm Hom}_\mathcal{T}(C,\bigoplus_{i\in I}Y_i)\end{equation*} is an isomorphism. The category ![]() $\mathcal{T}$ is called compactly generated if there exists a set
$\mathcal{T}$ is called compactly generated if there exists a set ![]() $\mathcal{S}\subseteq \mathcal{T}$ of compact objects such that for each
$\mathcal{S}\subseteq \mathcal{T}$ of compact objects such that for each ![]() $0\neq Y\in\mathcal{Y}$ there is a morphism
$0\neq Y\in\mathcal{Y}$ there is a morphism ![]() $0\neq f:\Sigma^m S\to Y$ for some
$0\neq f:\Sigma^m S\to Y$ for some ![]() $S\in\mathcal{S}$ and
$S\in\mathcal{S}$ and ![]() $m\in\mathbb{Z}$.
$m\in\mathbb{Z}$.
It follows by Liang and Wang [Reference Liang and Wang29, Theorem 1(a)] that the stable category ![]() $\mathcal{E}_0=\underline{\mathcal{GF}(R)\cap\mathcal{C}(R)}$ is compactly generated when R is right coherent with finite left global Gorenstein projective dimension. Based on their work, this property is inherited by the stable categories
$\mathcal{E}_0=\underline{\mathcal{GF}(R)\cap\mathcal{C}(R)}$ is compactly generated when R is right coherent with finite left global Gorenstein projective dimension. Based on their work, this property is inherited by the stable categories ![]() $\underline{\mathcal{PGF}(R)}$ and
$\underline{\mathcal{PGF}(R)}$ and ![]() $\underline{\mathcal{GF}_n(R)\cap\mathcal{C}_n(R)}$ for every integer
$\underline{\mathcal{GF}_n(R)\cap\mathcal{C}_n(R)}$ for every integer ![]() $n\geq 0$ under the weaker assumption that R has finite global Gorenstein AC-projective dimension. That is, the supremum of the
$n\geq 0$ under the weaker assumption that R has finite global Gorenstein AC-projective dimension. That is, the supremum of the ![]() $\mathcal{GP}_{AC}(R)$-resolution dimension of all R-modules,
$\mathcal{GP}_{AC}(R)$-resolution dimension of all R-modules,
is finite, where ![]() $\mathcal{GP}_{AC}(R)$ denotes the class of Gorenstein AC-projective modules in the sense of [Reference Bravo, Gillespie and Hovey7].
$\mathcal{GP}_{AC}(R)$ denotes the class of Gorenstein AC-projective modules in the sense of [Reference Bravo, Gillespie and Hovey7].
Corollary 3.8. There exist triangulated equivalences
Furthermore, if ![]() ${\rm GPD}_{AC}(R) \lt \infty$, then these triangulated categories are compactly generated.
${\rm GPD}_{AC}(R) \lt \infty$, then these triangulated categories are compactly generated.
Proof. By Theorem 3.6 and [Reference Saroch and Stovicek32, Theorem 4.9], we have the model structures
with the same trivial objects and the following inclusions
Applying [Reference Estrada and Gillespie17, Lemma 5.4], we get the following triangulated equivalences
On the other hand, following Corollary 3.7 and [Reference Saroch and Stovicek32, p. 27], we have
 \begin{equation*}
{\rm Ho}(\mathcal{M}_n)\backsimeq \underline{\mathcal{GF}_n(R)\cap \mathcal{C}_n(R)} \text{ and }{\rm Ho}(\mathcal{N})\backsimeq \underline{\mathcal{PGF}(R)}
\end{equation*}
\begin{equation*}
{\rm Ho}(\mathcal{M}_n)\backsimeq \underline{\mathcal{GF}_n(R)\cap \mathcal{C}_n(R)} \text{ and }{\rm Ho}(\mathcal{N})\backsimeq \underline{\mathcal{PGF}(R)}
\end{equation*}as triangulated categories. Hence, the first statement follows.
Finally, if ![]() ${\rm GPD}_{AC}(R) \lt \infty$, then our last claim follows by [Reference Liang and Wang29, Theorem 24, Proposition 21 and Corollary 33] and the above triangulated equivalences.
${\rm GPD}_{AC}(R) \lt \infty$, then our last claim follows by [Reference Liang and Wang29, Theorem 24, Proposition 21 and Corollary 33] and the above triangulated equivalences.
It is well-known that the stable categories ![]() $\underline{\mathcal{GP}(R)}$ and
$\underline{\mathcal{GP}(R)}$ and ![]() $\underline{\mathcal{GI}(R)}$ are triangulated categories. Li and Wang showed in [Reference Liang and Wang29, Theorem 1] that these triangulated categories are compactly generated whenever
$\underline{\mathcal{GI}(R)}$ are triangulated categories. Li and Wang showed in [Reference Liang and Wang29, Theorem 1] that these triangulated categories are compactly generated whenever ![]() ${\rm GPD}(R) \lt \infty$ with R right or left coherent. Their proof is mainly based on [Reference Liang and Wang29, Theorem 25]. However, the coherence assumption in [Reference Liang and Wang29, Theorem 25] is not needed if we replace
${\rm GPD}(R) \lt \infty$ with R right or left coherent. Their proof is mainly based on [Reference Liang and Wang29, Theorem 25]. However, the coherence assumption in [Reference Liang and Wang29, Theorem 25] is not needed if we replace ![]() ${\rm GPD}(R) \lt \infty$ with
${\rm GPD}(R) \lt \infty$ with ![]() ${\rm GPD}_{AC}(R) \lt \infty$. Therefore, following the same argument in [Reference Liang and Wang29, Corollary 34], we have the improved result:
${\rm GPD}_{AC}(R) \lt \infty$. Therefore, following the same argument in [Reference Liang and Wang29, Corollary 34], we have the improved result:
Corollary 3.9. Let R be a ring with ![]() ${\rm GPD}_{AC}(R) \lt \infty$. Then,
${\rm GPD}_{AC}(R) \lt \infty$. Then,
are compactly generated.
4. PGF dimension of modules and rings
In this section, we are interested in the PGF dimension of modules and rings and its connection with other homological dimensions.
The following result is a key result to prove many of the results that will follow. It is a combination of [Reference Stergiopoulou33, Theorem 3.20] and [Reference Dalezios and Emmanouil11, Theorem 3.4![]() $(i)\Leftrightarrow (ii)$], except for the last statement.
$(i)\Leftrightarrow (ii)$], except for the last statement.
Proposition 4.1. The following assertions are equivalent:
(1)
 ${\rm {PGF}\mbox{-}pd}_R(M)\leq n.$
${\rm {PGF}\mbox{-}pd}_R(M)\leq n.$(2) M is a direct summand in a module N such that there exists an exact sequence of R-modules
 \begin{equation*}0\to N\to X\to N\to 0\end{equation*}
\begin{equation*}0\to N\to X\to N\to 0\end{equation*}where
 ${\rm pd}_R(X)\leq n$ and
${\rm pd}_R(X)\leq n$ and  ${\rm Tor}_{n+1}^R(E,N)=0$ for any injective right R-module.
${\rm Tor}_{n+1}^R(E,N)=0$ for any injective right R-module.(3) There exists an exact sequence of R-modules
 \begin{equation*}0\to M\to X\to G\to 0\end{equation*}
\begin{equation*}0\to M\to X\to G\to 0\end{equation*}where
 $G\in\mathcal{PGF}(R)$ and
$G\in\mathcal{PGF}(R)$ and  ${\rm pd}_R(X)\leq n$.
${\rm pd}_R(X)\leq n$.
Consequently, ![]() $\mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}=\mathcal{P}_n(R).$
$\mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}=\mathcal{P}_n(R).$
Proof. (1) is equivalent to (2) by [Reference Stergiopoulou33, Theorem 3.20] and to (3) by [Reference Dalezios and Emmanouil11, Theorem 3.4]. We only have to prove the equality ![]() $\mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}=\mathcal{P}_n(R)$.
$\mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}=\mathcal{P}_n(R)$.
Clearly ![]() $\mathcal{P}_n(R)\subseteq \mathcal{PGF}_n(R)$ and by Lemma 3.2,
$\mathcal{P}_n(R)\subseteq \mathcal{PGF}_n(R)$ and by Lemma 3.2, ![]() $\mathcal{P}_n(R)\subseteq \mathcal{PGF}(R)^\perp$. Then,
$\mathcal{P}_n(R)\subseteq \mathcal{PGF}(R)^\perp$. Then, ![]() $\mathcal{P}_n(R)\subseteq \mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$. Conversely, if
$\mathcal{P}_n(R)\subseteq \mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$. Conversely, if ![]() $M\in\mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$, then there exists by (3) a split exact sequence of R-modules
$M\in\mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^{\perp}$, then there exists by (3) a split exact sequence of R-modules ![]() $0\to M\to X\to G\to 0$ where
$0\to M\to X\to G\to 0$ where ![]() $G\in\mathcal{PGF}(R)$ and
$G\in\mathcal{PGF}(R)$ and ![]() ${\rm pd}_R(X)\leq n$. Then,
${\rm pd}_R(X)\leq n$. Then, ![]() $M\in \mathcal{P}_n(R)$.
$M\in \mathcal{P}_n(R)$.
As a consequence, we get new characterizations of left (n-)perfect rings. Recall that [Reference Enochs, Jenda and López-Ramos16, Definition 2.1] a ring R is left n-perfect if every flat R-module has projective dimension at most n. In particular, left perfect rings are exactly left 0-perfect rings.
Theorem 4.2. A ring R is left n-perfect if and only every Gorenstein flat has PGF dimension at most n. In particular, the following assertions are equivalent:
(1) R is left perfect.
(2)
 $\mathcal{GF}(R)=\mathcal{PGF}(R)$.
$\mathcal{GF}(R)=\mathcal{PGF}(R)$.(3)
 $\mathcal{PGF}(R)$ is closed under direct limits.
$\mathcal{PGF}(R)$ is closed under direct limits.(4)
 $\left(\mathcal{PGF}(R),\mathcal{PGF}(R)^\perp\right) $ is a perfect cotorsion pair.
$\left(\mathcal{PGF}(R),\mathcal{PGF}(R)^\perp\right) $ is a perfect cotorsion pair.(5)
 $\mathcal{PGF}(R)$ is covering.
$\mathcal{PGF}(R)$ is covering.(6) Every Gorenstein flat R-module has a PGF cover.
(7) Every flat R-module has a projective cover.
Proof. ![]() $(\Leftarrow)$ Clearly
$(\Leftarrow)$ Clearly ![]() $\mathcal{F}(R)\subseteq \mathcal{GF}(R)\subseteq \mathcal{PGF}_n(R)$ and by Lemma 3.2,
$\mathcal{F}(R)\subseteq \mathcal{GF}(R)\subseteq \mathcal{PGF}_n(R)$ and by Lemma 3.2, ![]() $\mathcal{F}(R)\subseteq \mathcal{PGF}(R)^\perp$. Thus,
$\mathcal{F}(R)\subseteq \mathcal{PGF}(R)^\perp$. Thus, ![]() $\mathcal{F}(R)\subseteq \mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^\perp=\mathcal{P}_n(R)$ by Proposition 4.1. This means that R is left n-perfect.
$\mathcal{F}(R)\subseteq \mathcal{PGF}_n(R)\cap \mathcal{PGF}(R)^\perp=\mathcal{P}_n(R)$ by Proposition 4.1. This means that R is left n-perfect. ![]() $(\Rightarrow )$ Let M be a Gorenstein flat R-module. By [Reference Bennis and Mahdou5, Theorem 3.5 and Proposition 3.6], M is a direct summand in a module N such that there exists an exact sequence of R-modules
$(\Rightarrow )$ Let M be a Gorenstein flat R-module. By [Reference Bennis and Mahdou5, Theorem 3.5 and Proposition 3.6], M is a direct summand in a module N such that there exists an exact sequence of R-modules ![]() $0\to N\to F\to N\to 0$ with F flat and
$0\to N\to F\to N\to 0$ with F flat and ![]() ${\rm Tor}_{1}^R(E,N)=0$ for any injective right R-module. It follows that
${\rm Tor}_{1}^R(E,N)=0$ for any injective right R-module. It follows that  ${\rm Tor}_{k\geq 1}^R(E,N)\cong {\rm Tor}_{1}^R(E,N)=0$. Since
${\rm Tor}_{k\geq 1}^R(E,N)\cong {\rm Tor}_{1}^R(E,N)=0$. Since ![]() $F\in\mathcal{F}(R)\subseteq \mathcal{P}_n(R)$, it follows from Proposition 4.1 that
$F\in\mathcal{F}(R)\subseteq \mathcal{P}_n(R)$, it follows from Proposition 4.1 that ![]() $M\in \mathcal{PGF}_n(R)$.
$M\in \mathcal{PGF}_n(R)$.
We now prove the equivalences (1)–(7):
![]() $(1)\Leftrightarrow (2)$ By [Reference Saroch and Stovicek32, Theorem 4.9]. It also follows from the above equivalence.
$(1)\Leftrightarrow (2)$ By [Reference Saroch and Stovicek32, Theorem 4.9]. It also follows from the above equivalence.
![]() $(2)\Rightarrow (3)$ By Proposition 3.1(3).
$(2)\Rightarrow (3)$ By Proposition 3.1(3).
![]() $(3)\Rightarrow (4)$ By [Reference Saroch and Stovicek32, Theorem 4.9] and [Reference Göbel and Trlifaj19, Corollary 2.3.7].
$(3)\Rightarrow (4)$ By [Reference Saroch and Stovicek32, Theorem 4.9] and [Reference Göbel and Trlifaj19, Corollary 2.3.7].
![]() $(4)\Rightarrow (5)$ Clear.
$(4)\Rightarrow (5)$ Clear.
![]() $(5)\Rightarrow (6)$ Clear.
$(5)\Rightarrow (6)$ Clear.
![]() $(6)\Rightarrow (7)$ Let F be a flat R-module and
$(6)\Rightarrow (7)$ Let F be a flat R-module and ![]() $f:P\to F$ be a PGF cover. We claim that f is a projective cover. By Wakamatsu Lemma,
$f:P\to F$ be a PGF cover. We claim that f is a projective cover. By Wakamatsu Lemma, ![]() $K:={\rm Ker} f\in \mathcal{PGF}(R)^\perp$. But
$K:={\rm Ker} f\in \mathcal{PGF}(R)^\perp$. But ![]() $F\in\mathcal{F}(R)\subseteq \mathcal{PGF}(R)^\perp$ by Lemma 3.2 and
$F\in\mathcal{F}(R)\subseteq \mathcal{PGF}(R)^\perp$ by Lemma 3.2 and ![]() $\mathcal{PGF}(R)\cap \mathcal{PGF}(R)^\perp=\mathcal{P}(R)$ by Proposition 4.1. Hence,
$\mathcal{PGF}(R)\cap \mathcal{PGF}(R)^\perp=\mathcal{P}(R)$ by Proposition 4.1. Hence, ![]() $P\in \mathcal{PGF}(R)\cap \mathcal{PGF}(R)^\perp=\mathcal{P}(R)$. It remains to show that for any morphism
$P\in \mathcal{PGF}(R)\cap \mathcal{PGF}(R)^\perp=\mathcal{P}(R)$. It remains to show that for any morphism ![]() $g: P\to P$ such that fg = f, is an automorphism. But this holds true as f is a PGF cover.
$g: P\to P$ such that fg = f, is an automorphism. But this holds true as f is a PGF cover.
![]() $(7)\Rightarrow (1)$ By the proof of [Reference Enochs and Jenda15, Theorem 5.3.2(3)
$(7)\Rightarrow (1)$ By the proof of [Reference Enochs and Jenda15, Theorem 5.3.2(3)![]() $\Rightarrow$ (1)].
$\Rightarrow$ (1)].
Theorem 4.2 can be interpreted from the point of view of global dimensions. For this purpose (and for later use), we introduce the following homological invariant.
Definition 4.3. The global PGF dimension of R with respect to a class ![]() $\mathcal{X}\subseteq R$-Mod is defined as:
$\mathcal{X}\subseteq R$-Mod is defined as: ![]() ${\rm PGFD}_{\mathcal{X}}(R):={\rm sup}\{{\rm {PGF}\mbox{-}pd}_R(X)|X\in\mathcal{X}\}.$
${\rm PGFD}_{\mathcal{X}}(R):={\rm sup}\{{\rm {PGF}\mbox{-}pd}_R(X)|X\in\mathcal{X}\}.$
In particular, we set
and we simply call it the global PGF dimension of R.
We note that the global PGF dimension has been recently studied by Dalezios and Emmanouil [Reference Dalezios and Emmanouil11].
Corollary 4.4. A ring R is left n-perfect if and only if ![]() ${\rm PGFD}_{\mathcal{GF}(R)}(R)\leq n$.
${\rm PGFD}_{\mathcal{GF}(R)}(R)\leq n$.
In particular, R is left perfect if and only if ![]() ${\rm PGFD}_{\mathcal{GF}(R)}(R)=0$.
${\rm PGFD}_{\mathcal{GF}(R)}(R)=0$.
We now turn our attention to the questions raised in § 1.
Remark 4.5. Consider the following assertions:
(GP1) Any Gorenstein projective R-module is Gorenstein flat.
(GP2) Any R-module has a special Gorenstein projective precover.
(GP3) Any Gorenstein projective R-module is PGF, that is,
 $\mathcal{PGF}(R)=\mathcal{GP}(R).$
$\mathcal{PGF}(R)=\mathcal{GP}(R).$
It follows that (GP3) is equivalent to (GP1) by [Reference Iacob28, Theorem 3] and implies (GP2) by [Reference Saroch and Stovicek32, Theorem 4.9]. However, it is not clear whether (GP2) implies (GP1) or (GP3). Following this remark, our focus will be on (GP3).
Instead of asking whether any Gorenstein projective module is PGF or not, one could ask the following question:
(Q4): How far is a Gorenstein projective module from being PGF?
The following result reduces this problem to two cases.
Proposition 4.6. The PGF dimension of a Gorenstein projective R-module M is either zero or infinite.
Consequently, the global dimension ![]() ${\rm PGFD}_{\mathcal{GP}(R)}(R)$ is either zero or infinite.
${\rm PGFD}_{\mathcal{GP}(R)}(R)$ is either zero or infinite.
Proof. Assume ![]() $n={\rm {PGF}\mbox{-}pd}_R(M) \lt \infty$ and let us consider a special PGF precover (which exists by [Reference Saroch and Stovicek32, Theorem 4.9])
$n={\rm {PGF}\mbox{-}pd}_R(M) \lt \infty$ and let us consider a special PGF precover (which exists by [Reference Saroch and Stovicek32, Theorem 4.9]) ![]() $0\to N\to G\to M\to 0.$ By [Reference Dalezios and Emmanouil11, Proposition 2.4(ii)],
$0\to N\to G\to M\to 0.$ By [Reference Dalezios and Emmanouil11, Proposition 2.4(ii)], ![]() ${\rm {PGF}\mbox{-}pd}_R(N)\leq \mathrm{max}\{{\rm {PGF}\mbox{-}pd}_R(G),{\rm {PGF}\mbox{-}pd}_R(M)\}\leq n.$ Hence,
${\rm {PGF}\mbox{-}pd}_R(N)\leq \mathrm{max}\{{\rm {PGF}\mbox{-}pd}_R(G),{\rm {PGF}\mbox{-}pd}_R(M)\}\leq n.$ Hence, ![]() $N\in\mathcal{PGF}_n(R)\cap\mathcal{PGF}(R)^\perp=\mathcal{P}_n(R)$ by Proposition 4.1. Moreover, since
$N\in\mathcal{PGF}_n(R)\cap\mathcal{PGF}(R)^\perp=\mathcal{P}_n(R)$ by Proposition 4.1. Moreover, since ![]() $M\in\mathcal{GP}(R)$, there exists an exact sequence of R-modules
$M\in\mathcal{GP}(R)$, there exists an exact sequence of R-modules ![]() $0\to M\to P_{-1}\to \cdots \to P_{-n}\to L\to 0$ with each Pj projective. Hence,
$0\to M\to P_{-1}\to \cdots \to P_{-n}\to L\to 0$ with each Pj projective. Hence,  ${\rm Ext}^1_R(M,N)\cong {\rm Ext}^{n+1}_R(L,N)=0$ as
${\rm Ext}^1_R(M,N)\cong {\rm Ext}^{n+1}_R(L,N)=0$ as ![]() $N\in\mathcal{P}_n(R)$ and then the above short exact sequence splits. Therefore,
$N\in\mathcal{P}_n(R)$ and then the above short exact sequence splits. Therefore, ![]() $M\in \mathcal{PGF}(R)$ and this means that
$M\in \mathcal{PGF}(R)$ and this means that ![]() ${\rm {PGF}\mbox{-}pd}_R(M)=0$.
${\rm {PGF}\mbox{-}pd}_R(M)=0$.
In order to continue our investigations, we need the notion of definable classes. Recall from [Reference Prest31, Theorem 3.4.7] that a class of modules ![]() $\mathcal{D}$ is called definable if it is closed under direct products, direct limits and pure submodules. Such a class is, in particular, closed under direct sums and direct summands. We denote by
$\mathcal{D}$ is called definable if it is closed under direct products, direct limits and pure submodules. Such a class is, in particular, closed under direct sums and direct summands. We denote by ![]() $\langle\mathcal{X}\rangle$ the definable class generated by a class of modules
$\langle\mathcal{X}\rangle$ the definable class generated by a class of modules ![]() $\mathcal{X}$, that is, the smallest definable class containing
$\mathcal{X}$, that is, the smallest definable class containing ![]() $\mathcal{X}$. The definable closure
$\mathcal{X}$. The definable closure ![]() $\langle \mathcal{X}\rangle$ can be constructed, for instance, by closing
$\langle \mathcal{X}\rangle$ can be constructed, for instance, by closing ![]() $\mathcal{X}$ under direct products, then under pure submodules and, finally, under pure quotients. In case
$\mathcal{X}$ under direct products, then under pure submodules and, finally, under pure quotients. In case ![]() $\mathcal{X}=\{X\}$, we simply write
$\mathcal{X}=\{X\}$, we simply write ![]() $\langle\mathcal{X}\rangle=\langle X\rangle$.
$\langle\mathcal{X}\rangle=\langle X\rangle$.
It has been shown in many recent works [Reference Cortés-Izurdiaga and Saroch10, Reference Estrada, Iacob and Pérez18, Reference Saroch and Stovicek32] that the definable classes ![]() $\langle R\rangle$ and
$\langle R\rangle$ and ![]() $\langle R^+\rangle$ are of great importance. They will also be of interest to us. Thus, we propose the following definition, giving names to the modules belonging to these classes.
$\langle R^+\rangle$ are of great importance. They will also be of interest to us. Thus, we propose the following definition, giving names to the modules belonging to these classes.
Definition 4.7. An R-module is called definable flat if it belongs to the definable class ![]() $\langle R\rangle$. Dually, an R-module is called definable injective if it belongs to the definable class
$\langle R\rangle$. Dually, an R-module is called definable injective if it belongs to the definable class ![]() $\langle (R_R)^+\rangle$.
$\langle (R_R)^+\rangle$.
Clearly, ![]() $\langle R\rangle=\langle \mathcal{P}(R)\rangle=\langle \mathcal{F}(R)\rangle$ and
$\langle R\rangle=\langle \mathcal{P}(R)\rangle=\langle \mathcal{F}(R)\rangle$ and ![]() $\langle (_RR)^+\rangle=\langle\mathcal{I}(R^\mathrm{op})\rangle =\langle\mathcal{FI}(R^\mathrm{op})\rangle $. Moreover, R is right coherent if and only if definable flat R-modules coincide with flats if and only if definable injective right R-modules coincide withFP-injectives (see [Reference Prest31, Theorem 3.4.24]). Recall that a module M is called FP-injective if
$\langle (_RR)^+\rangle=\langle\mathcal{I}(R^\mathrm{op})\rangle =\langle\mathcal{FI}(R^\mathrm{op})\rangle $. Moreover, R is right coherent if and only if definable flat R-modules coincide with flats if and only if definable injective right R-modules coincide withFP-injectives (see [Reference Prest31, Theorem 3.4.24]). Recall that a module M is called FP-injective if ![]() $Ext^1(F,M)_0$ for every finitely presented module F.
$Ext^1(F,M)_0$ for every finitely presented module F.
As we will see next, the class of definable flat modules is a key point for extending many results from the class of coherent rings to a larger class of rings.
Lemma 4.8. Given an integer ![]() $n\geq 0$,
$n\geq 0$, ![]() ${\rm fd}_R(\langle R\rangle)\leq n$ if and only if the direct product of any family of flat R-modules has finite flat dimension
${\rm fd}_R(\langle R\rangle)\leq n$ if and only if the direct product of any family of flat R-modules has finite flat dimension ![]() $\leq n$.
$\leq n$.
Consequently, ![]() ${\rm fd}_R(\langle R\rangle)={\rm sup}\{{\rm fd}_R(\prod_iF_i)| (F_i)_i \text{is a family of flat } R\text{-modules} \}.$
${\rm fd}_R(\langle R\rangle)={\rm sup}\{{\rm fd}_R(\prod_iF_i)| (F_i)_i \text{is a family of flat } R\text{-modules} \}.$
Proof. (![]() $\Rightarrow $) For every family
$\Rightarrow $) For every family ![]() $(F_i)_i$ of flat R-modules, we have
$(F_i)_i$ of flat R-modules, we have ![]() $F_i\in\langle \mathcal{F}(R)\rangle=\langle R\rangle$ and since
$F_i\in\langle \mathcal{F}(R)\rangle=\langle R\rangle$ and since ![]() $\langle R\rangle$ is closed under products,
$\langle R\rangle$ is closed under products, ![]() $\prod_i F_i\in \langle R\rangle$. Hence,
$\prod_i F_i\in \langle R\rangle$. Hence, ![]() ${\rm fd}_R(\prod_iF_i)\leq{\rm fd}_R(\langle R\rangle)\leq n$. (
${\rm fd}_R(\prod_iF_i)\leq{\rm fd}_R(\langle R\rangle)\leq n$. (![]() $\Leftarrow$) Assume
$\Leftarrow$) Assume ![]() ${\rm fd}_R(\prod\mathcal{F}(R))\leq n$ and let
${\rm fd}_R(\prod\mathcal{F}(R))\leq n$ and let ![]() $X\in \langle R\rangle=\langle \mathcal{F}(R)\rangle$. The definable class
$X\in \langle R\rangle=\langle \mathcal{F}(R)\rangle$. The definable class ![]() $\langle \mathcal{F}(R)\rangle$ can be constructed by closing
$\langle \mathcal{F}(R)\rangle$ can be constructed by closing ![]() $\mathcal{F}(R)$ under products, then under pure submodules and finally under pure quotients. By hypothesis, any direct product of any family of flat R-modules belongs to
$\mathcal{F}(R)$ under products, then under pure submodules and finally under pure quotients. By hypothesis, any direct product of any family of flat R-modules belongs to ![]() $\mathcal{F}_n(R)$, and clearly
$\mathcal{F}_n(R)$, and clearly ![]() $\mathcal{F}_n(R)$ is closed under pure submodules and quotients (since a short exact sequence
$\mathcal{F}_n(R)$ is closed under pure submodules and quotients (since a short exact sequence ![]() $\mathcal{E}$ is pure if and only if its character
$\mathcal{E}$ is pure if and only if its character ![]() $\mathcal{E}^+$ is split). Hence,
$\mathcal{E}^+$ is split). Hence, ![]() $\langle R\rangle=\langle \mathcal{F}(R)\rangle \subseteq\mathcal{F}_n(R)$, that is,
$\langle R\rangle=\langle \mathcal{F}(R)\rangle \subseteq\mathcal{F}_n(R)$, that is, ![]() ${\rm fd}_R(\langle R\rangle)\leq n$.
${\rm fd}_R(\langle R\rangle)\leq n$.
Izurdiaga [Reference Cortés-Izurdiaga9] investigated rings for which the direct product of any family of flat R-modules has finite flat dimension. He calls them [Reference Cortés-Izurdiaga9, Section 4] right weak coherent rings. Moreover, if n is the maximum of the set consisting of all flat dimensions of all direct products of flat R-modules, then R is called right weak n-coherent. In particular, right weak 0-coherent rings are nothing but right coherent rings. It follows by Lemma 4.8 that R is right weak coherent if and only if and only if any definable flat module has finite flat dimension. In this case, R is right weak n-coherent with ![]() $n={\rm fd}_R(\langle R\rangle)$.
$n={\rm fd}_R(\langle R\rangle)$.
We also recall from [Reference Gillespie20] the notion of Ding projective modules (which are introduced for the first time in [Reference Ding, Li and Mao12] under a different name). An R-module M is called Ding projective if it is a syzygy of a ![]() ${\rm Hom}_R(-,\mathcal{F}(R))$-exact exact sequence of projective R-modules. The Ding projective dimension of an R-module M is defined as
${\rm Hom}_R(-,\mathcal{F}(R))$-exact exact sequence of projective R-modules. The Ding projective dimension of an R-module M is defined as ![]() ${\rm Dpd}_R(M)={\rm resdim}_{\mathcal{DP}(R)}(M)$ where
${\rm Dpd}_R(M)={\rm resdim}_{\mathcal{DP}(R)}(M)$ where ![]() $\mathcal{DP}(R)$ denotes the class of Ding projective R-modules.
$\mathcal{DP}(R)$ denotes the class of Ding projective R-modules.
As a consequence of the above lemma, the assumption that R is right coherent in [Reference Iacob28, Theorem 2] and [Reference Cortés-Izurdiaga and Saroch10, Corollary 5.10] can be replaced by that R is right weak coherent.
Corollary 4.9. Assume that R is a right weak coherent ring. Given an R-module M, we have ![]() ${\rm Dpd}_R(M)= {\rm {PGF}\mbox{-}pd}_R(M)$. In particular,
${\rm Dpd}_R(M)= {\rm {PGF}\mbox{-}pd}_R(M)$. In particular, ![]() $\mathcal{DP}(R)=\mathcal{PGF}(R)$ is the left hand of a complete cotorsion pair.
$\mathcal{DP}(R)=\mathcal{PGF}(R)$ is the left hand of a complete cotorsion pair.
Proof. We only need to show the equality ![]() $\mathcal{PGF}(R)=\mathcal{DP}(R)$. The inclusion
$\mathcal{PGF}(R)=\mathcal{DP}(R)$. The inclusion ![]() $\mathcal{PGF}(R)\subseteq \mathcal{DP}(R)$ holds for any ring R. For the other inequality, let
$\mathcal{PGF}(R)\subseteq \mathcal{DP}(R)$ holds for any ring R. For the other inequality, let ![]() $M\in\mathcal{DP}(R)$, then M is a syzygy of a
$M\in\mathcal{DP}(R)$, then M is a syzygy of a ![]() ${\rm Hom}_R(-,\mathcal{F}(R))-$exact exact sequence P of projective R-modules. Let X be a definable flat R-module. By Lemma 4.8,
${\rm Hom}_R(-,\mathcal{F}(R))-$exact exact sequence P of projective R-modules. Let X be a definable flat R-module. By Lemma 4.8, ![]() $m={\rm fd}_R(X) \lt \infty$. Then, X has a finite flat resolution
$m={\rm fd}_R(X) \lt \infty$. Then, X has a finite flat resolution
Applying the functor ![]() ${\rm Hom}_R(\textbf{P},-)$ to this exact sequence, we get an exact sequence of complexes
${\rm Hom}_R(\textbf{P},-)$ to this exact sequence, we get an exact sequence of complexes
As the class of exact complexes is thick, it follows that the complex ![]() ${\rm Hom}_R(\textbf{P},X)$ is exact and hence
${\rm Hom}_R(\textbf{P},X)$ is exact and hence ![]() $M\in\mathcal{PGF}(R)$.
$M\in\mathcal{PGF}(R)$.
The last claim follows by [Reference Saroch and Stovicek32, Theorem 4.9].
One could, as in Lemma 4.8, consider rings for which every definable flat has finite projective dimension. The following lemma, which we will use later, says that such rings are nothing new.
Lemma 4.10. ![]() ${\rm pd}_R(\langle R\rangle) \lt \infty$ if and only if R is left weak coherent and right n-perfect for some integer
${\rm pd}_R(\langle R\rangle) \lt \infty$ if and only if R is left weak coherent and right n-perfect for some integer ![]() $n\geq 0$.
$n\geq 0$.
Proof. ![]() $(\Rightarrow)$ Assume
$(\Rightarrow)$ Assume ![]() $n={\rm pd}_R(\langle R\rangle) \lt \infty$. Then,
$n={\rm pd}_R(\langle R\rangle) \lt \infty$. Then, ![]() ${\rm pd}_R(X)\leq n$ for all
${\rm pd}_R(X)\leq n$ for all ![]() $X\in \langle R\rangle$. In particular,
$X\in \langle R\rangle$. In particular, ![]() ${\rm fd}_R(X)\leq {\rm pd}_R(X)\leq n$ for all
${\rm fd}_R(X)\leq {\rm pd}_R(X)\leq n$ for all ![]() $X\in \langle R\rangle$ and
$X\in \langle R\rangle$ and ![]() ${\rm pd}_R(X)\leq n$ for all
${\rm pd}_R(X)\leq n$ for all ![]() $X\in\mathcal{F}(R)\subseteq \langle R\rangle$.
$X\in\mathcal{F}(R)\subseteq \langle R\rangle$. ![]() $(\Leftarrow)$ Assume that
$(\Leftarrow)$ Assume that ![]() $m={\rm fd}_R(\langle R\rangle) \lt \infty$. Given a partial projective resolution of an R-module
$m={\rm fd}_R(\langle R\rangle) \lt \infty$. Given a partial projective resolution of an R-module ![]() $M\in \langle R\rangle$
$M\in \langle R\rangle$
we get that Km is flat and hence ![]() ${\rm pd}_R(K_m)\leq n$ as
${\rm pd}_R(K_m)\leq n$ as ![]() $K_m\in \langle R\rangle$. Therefore,
$K_m\in \langle R\rangle$. Therefore, ![]() ${\rm pd}_R(M)\leq n+m$. Thus,
${\rm pd}_R(M)\leq n+m$. Thus, ![]() ${\rm pd}_R(\langle R\rangle)\leq n+m \lt \infty$.
${\rm pd}_R(\langle R\rangle)\leq n+m \lt \infty$.
Now we are ready to give a partial answer to Question (Q3) raised in § 1. Recall that a ![]() ${\rm Hom}_R(-,\mathcal{P}(R))$-exact exact complex of projective modules is called totally acyclic complex of projectives.
${\rm Hom}_R(-,\mathcal{P}(R))$-exact exact complex of projective modules is called totally acyclic complex of projectives.
Proposition 4.11. ![]() $\mathcal{PGF}(R)=\mathcal{GP}(R)$ if and only if any totally acyclic complex of projectives is
$\mathcal{PGF}(R)=\mathcal{GP}(R)$ if and only if any totally acyclic complex of projectives is ![]() ${\rm Hom}_R(-,\langle R\rangle)$-exact if and only if any totally acyclic complex of projectives is
${\rm Hom}_R(-,\langle R\rangle)$-exact if and only if any totally acyclic complex of projectives is ![]() $(\mathcal{I}(R^{op})\otimes-)$-exact.
$(\mathcal{I}(R^{op})\otimes-)$-exact.
In particular, this is the case if one of the following holds:
(a) R is right weak coherent and left n-perfect for some integer
 $n\geq 0$.
$n\geq 0$.(b) R is a ring where any injective right R-module has finite flat dimension.
Proof. The equivalences follow immediately from [Reference Saroch and Stovicek32, Corollary 4.5].
(a) By above, it suffices to show that any totally acyclic complex of projectives P is ![]() ${\rm Hom}_R(-,X)$-exact for any definable flat R-module X. But, this can be shown as in the proof of Corollary 4.9, using a finite projective resolution of X which exists by assumption and Lemma 4.10.
${\rm Hom}_R(-,X)$-exact for any definable flat R-module X. But, this can be shown as in the proof of Corollary 4.9, using a finite projective resolution of X which exists by assumption and Lemma 4.10.
(b) Follows by [Reference Iacob28, Proposition 9].
(i) Notice that the assertion ‘any totally acyclic complex of projectives is
 ${\rm Hom}_R(-,\langle R\rangle)$-exact’ is equivalent to
${\rm Hom}_R(-,\langle R\rangle)$-exact’ is equivalent to  $\langle R\rangle\subseteq \mathcal{GP}(R)^\perp$. Therefore, Proposition 4.11 improves [Reference Iacob28, Theorem 4] in the sense that if we replace the class of flat modules with that of definable flat we can drop the coherence assumption. We also note that every right coherent ring is right weak coherent, so the example in Proposition 4.11(a) is more general.
$\langle R\rangle\subseteq \mathcal{GP}(R)^\perp$. Therefore, Proposition 4.11 improves [Reference Iacob28, Theorem 4] in the sense that if we replace the class of flat modules with that of definable flat we can drop the coherence assumption. We also note that every right coherent ring is right weak coherent, so the example in Proposition 4.11(a) is more general.(ii) In view of Proposition 4.11, Remark 4.5 and Theorem 4.2, if R is right weak coherent, then R is left perfect if and only if
 $\mathcal{GP}(R)=\mathcal{GF}(R)$. This result improves [Reference Bravo, Gillespie and Hovey8, Theorem 4.5
$\mathcal{GP}(R)=\mathcal{GF}(R)$. This result improves [Reference Bravo, Gillespie and Hovey8, Theorem 4.5  $(i)\Leftrightarrow (iv)$].
$(i)\Leftrightarrow (iv)$].
Consequently, partial answers to questions (Q1) and (Q2) are obtained.
Corollary 4.13. Assume that R satisfies the equivalent conditions of Proposition 4.11.
(1) For any R-module M, we have
 ${\rm Gfd}_R(M)\leq {\rm Gpd}_R(M)$.
${\rm Gfd}_R(M)\leq {\rm Gpd}_R(M)$.In particular, every Gorenstein projective R-module is Gorenstein flat.
(2)
 $(\mathcal{GP}(R),\mathcal{GP}(R)^\perp)$ is a complete hereditary cotorsion pair.
$(\mathcal{GP}(R),\mathcal{GP}(R)^\perp)$ is a complete hereditary cotorsion pair.In particular, every R-module has a special Gorenstein projective precover.
Proof. (1) We only need to show that ![]() $\mathcal{GP}(R)\subseteq \mathcal{GF}(R)$. But this follows by Proposition 4.16 as
$\mathcal{GP}(R)\subseteq \mathcal{GF}(R)$. But this follows by Proposition 4.16 as ![]() $\mathcal{GP}(R)=\mathcal{PGF}(R)\subseteq \mathcal{GF}(R)$.
$\mathcal{GP}(R)=\mathcal{PGF}(R)\subseteq \mathcal{GF}(R)$.
(2) Follows by Proposition 4.11 and [Reference Saroch and Stovicek32, Theorem 4.9].
We now focus our attention on the global PGF dimension of R. As a first result, we provide simple ways to compute it (compare with [Reference Dalezios and Emmanouil11, Theorem 5.1]).
Theorem 4.14. The following assertions are equivalent:
(1)
 ${\rm PGFD}(R)\leq n$.
${\rm PGFD}(R)\leq n$.(2) The following two assertions hold.
(i)
 ${\rm id}_R(M)\leq n$ for every definable flat R-module M.
${\rm id}_R(M)\leq n$ for every definable flat R-module M.(ii)
 ${\rm pd}_R(M)\leq n$ for every injective R-module M.
${\rm pd}_R(M)\leq n$ for every injective R-module M.
(3) The following two assertions hold.
(i)
 ${\rm fd}_{R^{op}}(M)\leq n$ for every definable injective right R-module M.
${\rm fd}_{R^{op}}(M)\leq n$ for every definable injective right R-module M.(ii)
 ${\rm pd}_R(M)\leq n$ for every injective R-module M.
${\rm pd}_R(M)\leq n$ for every injective R-module M.
(4) The following two assertions hold.
(i)
 ${\rm fd}_{R^{op}}(M)\leq n$ for every (FP-)injective right R-module M.
${\rm fd}_{R^{op}}(M)\leq n$ for every (FP-)injective right R-module M.(ii)
 ${\rm pd}_R(M)\leq n$ for every injective R-module M.
${\rm pd}_R(M)\leq n$ for every injective R-module M.
Consequently, the global PGF dimension of R can be computed by the following formulas:
 \begin{align*}
{\rm PGFD}(R)&= max\{{\rm pd}_R(\mathcal{I}(R)),{\rm id}_R(\langle R\rangle)\}\\
&= max\{{\rm pd}_R(\mathcal{I}(R)),{\rm fd}_{R^{op}}(\langle R^+\rangle)\}\\
&= max\{{\rm pd}_R(\mathcal{I}(R),{\rm fd}_{R^{op}}(\mathcal{I}(R^{op}))\}.
\end{align*}
\begin{align*}
{\rm PGFD}(R)&= max\{{\rm pd}_R(\mathcal{I}(R)),{\rm id}_R(\langle R\rangle)\}\\
&= max\{{\rm pd}_R(\mathcal{I}(R)),{\rm fd}_{R^{op}}(\langle R^+\rangle)\}\\
&= max\{{\rm pd}_R(\mathcal{I}(R),{\rm fd}_{R^{op}}(\mathcal{I}(R^{op}))\}.
\end{align*}Proof. ![]() $1.\Rightarrow 2.$ (a) Consider an R-module N and a finite PGF resolution:
$1.\Rightarrow 2.$ (a) Consider an R-module N and a finite PGF resolution:
By [Reference Saroch and Stovicek32, Corollary 4.5],  ${\rm Ext}^{k\geq 1}_R(G_i,M)=0$ for any
${\rm Ext}^{k\geq 1}_R(G_i,M)=0$ for any ![]() $M\in\langle R\rangle$ and i. Hence,
$M\in\langle R\rangle$ and i. Hence,  ${\rm Ext}^{n+1}_R(N,M)\cong {\rm Ext}_R^1(G_n,M)=0$. Then,
${\rm Ext}^{n+1}_R(N,M)\cong {\rm Ext}_R^1(G_n,M)=0$. Then, ![]() ${\rm id}_R(M)\leq n$.
${\rm id}_R(M)\leq n$.
(b) Let M be an injective R-module. Since ![]() ${\rm {PGF}\mbox{-}pd}_R(M)\leq n$, there exists a split short exact sequence
${\rm {PGF}\mbox{-}pd}_R(M)\leq n$, there exists a split short exact sequence ![]() $0\to M\to X\to G\to 0$ with
$0\to M\to X\to G\to 0$ with ![]() ${\rm pd}_R(X)\leq n$ by Proposition 4.1(3). Hence,
${\rm pd}_R(X)\leq n$ by Proposition 4.1(3). Hence, ![]() ${\rm pd}_R(M)\leq n$.
${\rm pd}_R(M)\leq n$.
![]() $2.\Rightarrow 3.$ We only prove (a) as (b) is clear. For any definable injective right R-module M, we have
$2.\Rightarrow 3.$ We only prove (a) as (b) is clear. For any definable injective right R-module M, we have ![]() ${\rm fd}_{R^\mathrm{op}}(M)\leq n$ if and only if
${\rm fd}_{R^\mathrm{op}}(M)\leq n$ if and only if  ${\rm Tor}^R_{n+1}(M,-)=0$ if and only if
${\rm Tor}^R_{n+1}(M,-)=0$ if and only if  $ {\rm Ext}_R^{n+1}(-,M^+)\cong{\rm Tor}^R_{n+1}(M,-)^+=0$ if and only
$ {\rm Ext}_R^{n+1}(-,M^+)\cong{\rm Tor}^R_{n+1}(M,-)^+=0$ if and only ![]() ${\rm id}_R(M^+)\leq n$. This later holds by 2(a) and [Reference Estrada, Iacob and Pérez18, Remark 2.10] as
${\rm id}_R(M^+)\leq n$. This later holds by 2(a) and [Reference Estrada, Iacob and Pérez18, Remark 2.10] as ![]() $M^+\in\langle R\rangle$. Hence,
$M^+\in\langle R\rangle$. Hence, ![]() ${\rm fd}_{R^\mathrm{op}}(M)\leq n$.
${\rm fd}_{R^\mathrm{op}}(M)\leq n$.
![]() $3.\Rightarrow 4.$ (b) is clear and (a) follows by
$3.\Rightarrow 4.$ (b) is clear and (a) follows by ![]() $\mathcal{I}({R^\mathrm{op}})\subseteq \mathcal{FI}({R^\mathrm{op}})\subseteq \langle \mathcal{FI}({R^\mathrm{op}})\rangle= \langle (R_R)^+\rangle$.
$\mathcal{I}({R^\mathrm{op}})\subseteq \mathcal{FI}({R^\mathrm{op}})\subseteq \langle \mathcal{FI}({R^\mathrm{op}})\rangle= \langle (R_R)^+\rangle$.
![]() $4.\Rightarrow 1.$ Let M be an R-module. Consider a projective and an injective resolution of M:
$4.\Rightarrow 1.$ Let M be an R-module. Consider a projective and an injective resolution of M:
respectively. Decomposing these exact sequences into short exact ones we get, for every integer ![]() $i\in {\mathbb{N}}$,
$i\in {\mathbb{N}}$,
where ![]() $L_i={\rm Coker}(P_{i+1}\to P_{i})$ and
$L_i={\rm Coker}(P_{i+1}\to P_{i})$ and ![]() $K_i={\rm Ker}(I_i\to I_{i+1})$. Note that
$K_i={\rm Ker}(I_i\to I_{i+1})$. Note that ![]() $M=L_0=K_0$. Adding the direct sum of the first sequences,
$M=L_0=K_0$. Adding the direct sum of the first sequences,
 \begin{equation*}0 \to \bigoplus_{i\in{\mathbb{N}}}L_{i+1}\to \bigoplus_{i\in{\mathbb{N}}}P_i\to M\oplus( \bigoplus_{i\in{\mathbb{N}}}L_{i+1})\to 0\end{equation*}
\begin{equation*}0 \to \bigoplus_{i\in{\mathbb{N}}}L_{i+1}\to \bigoplus_{i\in{\mathbb{N}}}P_i\to M\oplus( \bigoplus_{i\in{\mathbb{N}}}L_{i+1})\to 0\end{equation*}to the direct product of the second ones,
 \begin{equation*}0\to M\oplus( \prod_{i\in{\mathbb{N}}}K_{i+1})\to \prod_{i\in{\mathbb{N}}}I_i\to \prod_{i\in{\mathbb{N}}}K_{i+1}\to 0\end{equation*}
\begin{equation*}0\to M\oplus( \prod_{i\in{\mathbb{N}}}K_{i+1})\to \prod_{i\in{\mathbb{N}}}I_i\to \prod_{i\in{\mathbb{N}}}K_{i+1}\to 0\end{equation*} we get an exact sequence of the form ![]() $0\to N\to X\to N\to 0$, where
$0\to N\to X\to N\to 0$, where
 \begin{equation*}X=(\bigoplus_{i\in N} P_i)\oplus (\prod_{i\in N} I_i)\text{ and } N=M\oplus \left((\bigoplus_{i\in N} L_{i+1}) \oplus (\prod_{i\in N} K_{i+1})\right).\end{equation*}
\begin{equation*}X=(\bigoplus_{i\in N} P_i)\oplus (\prod_{i\in N} I_i)\text{ and } N=M\oplus \left((\bigoplus_{i\in N} L_{i+1}) \oplus (\prod_{i\in N} K_{i+1})\right).\end{equation*} By (b), ![]() ${\rm pd}_R(X)={\rm pd}_R((\prod_{i\in N} I_i))\leq n$ and by (a),
${\rm pd}_R(X)={\rm pd}_R((\prod_{i\in N} I_i))\leq n$ and by (a),  ${\rm Tor}^R_{n+1}(E,N)=0$ for any injective right R-module E. And since M is a direct summand in N, it follows from Proposition 4.1 that
${\rm Tor}^R_{n+1}(E,N)=0$ for any injective right R-module E. And since M is a direct summand in N, it follows from Proposition 4.1 that ![]() ${\rm {PGF}\mbox{-}pd}_R(M)\leq n$ as desired.
${\rm {PGF}\mbox{-}pd}_R(M)\leq n$ as desired.
Global dimensions of rings are known to characterize classical rings. And the global PGF dimension is no exception. Recall that a ring R is called quasi-Frobenius if injective left (respectively, right) R-modules coincide with projective left (respectively, right) modules.
Corollary 4.15. ![]() ${\rm PGFD}(R)=0$ if and only if R is quasi-Frobenius.
${\rm PGFD}(R)=0$ if and only if R is quasi-Frobenius.
Proof. ![]() $(\Rightarrow)$ By Theorem 4.14(2), we have
$(\Rightarrow)$ By Theorem 4.14(2), we have ![]() $\mathcal{P}(R)\subseteq \langle R\rangle\subseteq \mathcal{I}(R)$ and
$\mathcal{P}(R)\subseteq \langle R\rangle\subseteq \mathcal{I}(R)$ and ![]() $\mathcal{I}(R)\subseteq \mathcal{P}(R)$. Then,
$\mathcal{I}(R)\subseteq \mathcal{P}(R)$. Then, ![]() $\mathcal{P}(R)=\mathcal{I}(R)$ and therefore R is quasi-Frobenius.
$\mathcal{P}(R)=\mathcal{I}(R)$ and therefore R is quasi-Frobenius. ![]() $(\Leftarrow)$ If R is quasi-Frobenius, then
$(\Leftarrow)$ If R is quasi-Frobenius, then ![]() $\mathcal{I}(R)=\mathcal{P}(R)$ and
$\mathcal{I}(R)=\mathcal{P}(R)$ and ![]() $\mathcal{I}(R^\mathrm{op})=\mathcal{P}(R^\mathrm{op})\subseteq \mathcal{F}(R^\mathrm{op})$. Hence,
$\mathcal{I}(R^\mathrm{op})=\mathcal{P}(R^\mathrm{op})\subseteq \mathcal{F}(R^\mathrm{op})$. Hence, ![]() ${\rm PGFD}(R)=0$ by Theorem 4.14(4).
${\rm PGFD}(R)=0$ by Theorem 4.14(4).
At this point, it is natural to ask what the relationship between the global PGF dimension and the global Gorenstein projective dimension could be. Clearly, ![]() ${\rm GPD}(R)\leq {\rm PGFD}(R)$ as
${\rm GPD}(R)\leq {\rm PGFD}(R)$ as ![]() $\mathcal{PGF}(R)\subseteq \mathcal{GP}(R)$. Over an (Iwanaga-)Gorenstein ring R, it is an immediate consequence of Huang [Reference Huang25, Theorems 4.9 and 4.13] that we have an equality
$\mathcal{PGF}(R)\subseteq \mathcal{GP}(R)$. Over an (Iwanaga-)Gorenstein ring R, it is an immediate consequence of Huang [Reference Huang25, Theorems 4.9 and 4.13] that we have an equality ![]() ${\rm GPD}(R)={\rm PGFD}(R)$. Dalezios and Emmanouil, on the other hand, have shown in [Reference Dalezios and Emmanouil11, Theorem 5.1] this equality when R has finite global PGF dimension.
${\rm GPD}(R)={\rm PGFD}(R)$. Dalezios and Emmanouil, on the other hand, have shown in [Reference Dalezios and Emmanouil11, Theorem 5.1] this equality when R has finite global PGF dimension.
Our last main result gives a positive answer to this question for any ring R. It is worth noting that the following result, as pointed out to me by Sergio Estrada, is contained in the proof of a recent result by Wang, Yang, Shao and Zhang [Reference Wang, Yang, Shao and Zhang34, Theorem 3.7]. However, our proof is different.
Theorem 4.16. The global Gorenstein projective dimension of R coincides with the global PGF dimension of R. That is, ![]() ${\rm GPD}(R)={\rm PGFD}(R).$
${\rm GPD}(R)={\rm PGFD}(R).$
Proof. The inequality ![]() ${\rm GPD}(R)\leq {\rm PGFD}(R)$ is clear since
${\rm GPD}(R)\leq {\rm PGFD}(R)$ is clear since ![]() $\mathcal{PGF}(R)\subseteq \mathcal{GP}(R)$. If
$\mathcal{PGF}(R)\subseteq \mathcal{GP}(R)$. If ![]() ${\rm GPD}(R)=\infty$, then
${\rm GPD}(R)=\infty$, then ![]() ${\rm PGFD}(R)={\rm GPD}(R)$ and we are done.
${\rm PGFD}(R)={\rm GPD}(R)$ and we are done.
Assume ![]() $n={\rm GPD}(R) \lt \infty$. By [Reference Bennis and Mahdou6, Corollary 2.7],
$n={\rm GPD}(R) \lt \infty$. By [Reference Bennis and Mahdou6, Corollary 2.7], ![]() ${\rm pd}_R(E)\leq n$ for every injective R-module E. On the other hand, following [Reference Cortés-Izurdiaga9, Examples 4.4(3)], R is right weak coherent. It follows that
${\rm pd}_R(E)\leq n$ for every injective R-module E. On the other hand, following [Reference Cortés-Izurdiaga9, Examples 4.4(3)], R is right weak coherent. It follows that ![]() ${\rm fd}_R(\langle R\rangle) \lt \infty$ by Lemma 4.8. This implies that
${\rm fd}_R(\langle R\rangle) \lt \infty$ by Lemma 4.8. This implies that ![]() ${\rm id}_R(\langle R\rangle)\leq n$ by [Reference Bennis and Mahdou6, Corollary 2.7]. Applying now Theorem 4.14(2), we get that
${\rm id}_R(\langle R\rangle)\leq n$ by [Reference Bennis and Mahdou6, Corollary 2.7]. Applying now Theorem 4.14(2), we get that ![]() ${\rm PGFD}(R)\leq n$.
${\rm PGFD}(R)\leq n$.
We end the paper with some consequences of Theorem 4.16.
Gorenstein injective modules are seen as dual to Gorenstein projective modules. Based on this, one could introduce a dual notion of a PGF module. Let us call an R-module Gorenstein definable injective if it is a syzygy of a ![]() ${\rm Hom}_R(\langle R^+\rangle,-)$-exact exact sequence of injective R-modules. Define its Gorenstein definable injective dimension as
${\rm Hom}_R(\langle R^+\rangle,-)$-exact exact sequence of injective R-modules. Define its Gorenstein definable injective dimension as ![]() ${\rm Gdid}(M)={\rm resdim}_{\mathcal{GDI}(R)}(M)$ where
${\rm Gdid}(M)={\rm resdim}_{\mathcal{GDI}(R)}(M)$ where ![]() $\mathcal{GDI}(R)$ denotes the class of all Gorenstein definable injective R-modules.
$\mathcal{GDI}(R)$ denotes the class of all Gorenstein definable injective R-modules.
It is known that the global dimension of R can be computed either by projective or injective dimensions, that is, the following equality holds:
This fact was extended to the Gorenstein setting by Enochs and Jenda [Reference Enochs and Jenda15, Section 12.3] for (Iwanaga-)Gorenstein rings and later by Bennis and Mahdou [Reference Bennis and Mahdou6, Theorem 1.1] for any ring.
Inspired by this, one could ask whether the equality
holds true as well?
Using again Theorem 4.16, we give a positive answer to this question.
Corollary 4.17. For any ring R, we have the following equalities:
with ![]() ${\rm GDID}(R):={\rm sup}\{\rm {Gdid}_R(M)|M \text{is an }R\text{-module}\}.$
${\rm GDID}(R):={\rm sup}\{\rm {Gdid}_R(M)|M \text{is an }R\text{-module}\}.$
Proof. First, we have the equality ![]() ${\rm PGFD}(R)={\rm GID}(R)$ that follows by Theorem 4.16 and [Reference Bennis and Mahdou6, Theorem 1.1].
${\rm PGFD}(R)={\rm GID}(R)$ that follows by Theorem 4.16 and [Reference Bennis and Mahdou6, Theorem 1.1].
Clearly, ![]() ${\rm GID}(R)\leq {\rm sup}\{{\rm Gdid}(M)|M\in R\text{-Mod}\}$ since
${\rm GID}(R)\leq {\rm sup}\{{\rm Gdid}(M)|M\in R\text{-Mod}\}$ since ![]() $\mathcal{GDI}(R)\subseteq \mathcal{GI}(R)$. Assume now that
$\mathcal{GDI}(R)\subseteq \mathcal{GI}(R)$. Assume now that ![]() $n={\rm GID}(R) \lt \infty$. If we prove that
$n={\rm GID}(R) \lt \infty$. If we prove that ![]() ${\rm id}_R(M) \lt \infty$ for any definable injective R-module M, we are done, as this condition implies that
${\rm id}_R(M) \lt \infty$ for any definable injective R-module M, we are done, as this condition implies that ![]() $\mathcal{GI}(R)=\mathcal{GDI}(R)$. Following [Reference Bennis and Mahdou6, Corollary 2.7], it suffices to show that
$\mathcal{GI}(R)=\mathcal{GDI}(R)$. Following [Reference Bennis and Mahdou6, Corollary 2.7], it suffices to show that ![]() ${\rm fd}_R(M) \lt \infty$ for any definable injective R-module. But, using [Reference Cortés-Izurdiaga and Saroch10, Lemma 5.6(1)], it suffices to show that
${\rm fd}_R(M) \lt \infty$ for any definable injective R-module. But, using [Reference Cortés-Izurdiaga and Saroch10, Lemma 5.6(1)], it suffices to show that ![]() ${\rm fd}_R(M) \lt \infty$ for every FP-injective R-module M.
${\rm fd}_R(M) \lt \infty$ for every FP-injective R-module M.
Let ![]() $_RM$ be FP-injective. Then, there exists a pure monomorphism
$_RM$ be FP-injective. Then, there exists a pure monomorphism ![]() $0\to M \hookrightarrow E$ with
$0\to M \hookrightarrow E$ with ![]() $_RE$ injective. Using again [Reference Bennis and Mahdou6, Corollary 2.7], we get that
$_RE$ injective. Using again [Reference Bennis and Mahdou6, Corollary 2.7], we get that ![]() ${\rm fd}_R(E)\leq n$ and hence
${\rm fd}_R(E)\leq n$ and hence ![]() ${\rm fd}_R(M)\leq {\rm fd}_R(E)\leq n \lt \infty$ as desired.
${\rm fd}_R(M)\leq {\rm fd}_R(E)\leq n \lt \infty$ as desired.
Remark 4.18. It clear by the definitions that we have the inequalities
 \begin{align*}
{\rm GPD}(R) & \leq {\rm DPD}(R) \leq{\rm PGFD}(R)\leq {\rm GPD}_{AC}(R),\\
{\rm GID}(R) & \leq {\rm DID}(R) \leq{\rm GDID}(R)\leq {\rm GID}_{AC}(R)
\end{align*}
\begin{align*}
{\rm GPD}(R) & \leq {\rm DPD}(R) \leq{\rm PGFD}(R)\leq {\rm GPD}_{AC}(R),\\
{\rm GID}(R) & \leq {\rm DID}(R) \leq{\rm GDID}(R)\leq {\rm GID}_{AC}(R)
\end{align*}with
 \begin{align*}
{\rm DPD}(R) & :={\rm sup}\{{\rm Dpd}_R(M)| M \text{is an }R\text{-module} \},\\
{\rm DID}(R) & :={\rm sup}\{{\rm Did}_R(M)| M \text{is an }R\text{-module} \},\\
{\rm GPD}_{AC}(R) & :={\rm sup}\{{\rm resdim}_{\mathcal{GI}_{AC}(R)}(M)| M \text{is an }R\text{-module} \},
\end{align*}
\begin{align*}
{\rm DPD}(R) & :={\rm sup}\{{\rm Dpd}_R(M)| M \text{is an }R\text{-module} \},\\
{\rm DID}(R) & :={\rm sup}\{{\rm Did}_R(M)| M \text{is an }R\text{-module} \},\\
{\rm GPD}_{AC}(R) & :={\rm sup}\{{\rm resdim}_{\mathcal{GI}_{AC}(R)}(M)| M \text{is an }R\text{-module} \},
\end{align*} where ![]() $\mathcal{GI}_{AC}(R)$ denotes the class of all Gorenstein AC-injective modules in the sense of [Reference Bravo, Gillespie and Hovey7].
$\mathcal{GI}_{AC}(R)$ denotes the class of all Gorenstein AC-injective modules in the sense of [Reference Bravo, Gillespie and Hovey7].
As stated above, Bennis and Mahdou showed in [Reference Bennis and Mahdou6, Theorem 1.1] the equality ![]() ${\rm GPD}(R)={\rm GID}(R)$ for any ring R. Generally, Huerta, Mendoza and Pérez have recently shown in [Reference Huerta, Mendoza and Pérez26, Corollary 8.8] the following equalities:
${\rm GPD}(R)={\rm GID}(R)$ for any ring R. Generally, Huerta, Mendoza and Pérez have recently shown in [Reference Huerta, Mendoza and Pérez26, Corollary 8.8] the following equalities:
The result [Reference Huerta, Mendoza and Pérez26, Corollary 8.8] is based on [Reference Huerta, Mendoza and Pérez26, Lemma 8.1], which is stated incorrectly as indicated in the corrigendum [Reference Huerta, Mendoza and Pérez27]. So, the result [Reference Huerta, Mendoza and Pérez26, Corollary 8.8] is no longer available and the question of whether the equalities ![]() ${\rm DPD}(R)={\rm DID}(R)$ and
${\rm DPD}(R)={\rm DID}(R)$ and ![]() ${\rm GPD}_{AC}(R)={\rm GID}_{AC}(R)$ hold for any ring R is still open. However, following Corollary 4.17, we have a positive answer for the second equality. Generally, we have the following equalities for any ring R:
${\rm GPD}_{AC}(R)={\rm GID}_{AC}(R)$ hold for any ring R is still open. However, following Corollary 4.17, we have a positive answer for the second equality. Generally, we have the following equalities for any ring R:
Auslander’s theorem on the global dimension states that we can compute the global dimension of R by just computing the projective dimension of cyclic R-modules. That is, the formula ![]() ${\rm gldim}(R)={\rm sup}\{{\rm pd}_R(R/I)|I \text{ is a left idea}\}$ holds true. Bennis, Hu and Wang [Reference Bennis, Hu and Wang4, Theorem 1.1] extended this formula to the Gorenstein setting for commutative rings. However, one can see that the same proof also holds for non-commutative rings. Taking advantage of this fact, together with Theorem 4.16, we get a PGF version of Auslander’s theorem.
${\rm gldim}(R)={\rm sup}\{{\rm pd}_R(R/I)|I \text{ is a left idea}\}$ holds true. Bennis, Hu and Wang [Reference Bennis, Hu and Wang4, Theorem 1.1] extended this formula to the Gorenstein setting for commutative rings. However, one can see that the same proof also holds for non-commutative rings. Taking advantage of this fact, together with Theorem 4.16, we get a PGF version of Auslander’s theorem.
Corollary 4.19. (Auslander’s theorem on the global PGF dimension)
For any ring R, we have the following formula:
Proof. The inequality ![]() $\{{\rm {PGF}\mbox{-}pd}_R(R/I)|I \text{ is a left ideal}\}\leq {\rm PGFD}(R)$ is clear. We may assume that
$\{{\rm {PGF}\mbox{-}pd}_R(R/I)|I \text{ is a left ideal}\}\leq {\rm PGFD}(R)$ is clear. We may assume that ![]() $n={\rm sup}\{{\rm {PGF}\mbox{-}pd}_R(R/I)|I \text{ is a left ideal}\} \lt \infty$. Since
$n={\rm sup}\{{\rm {PGF}\mbox{-}pd}_R(R/I)|I \text{ is a left ideal}\} \lt \infty$. Since ![]() $\mathcal{PGF}(R)\subseteq \mathcal{GP}(R)$, we have
$\mathcal{PGF}(R)\subseteq \mathcal{GP}(R)$, we have ![]() ${\rm Gpd}(R/I)\leq {\rm {PGF}\mbox{-}pd}_R(R/I)\leq n$ for every left ideal I, and therefore
${\rm Gpd}(R/I)\leq {\rm {PGF}\mbox{-}pd}_R(R/I)\leq n$ for every left ideal I, and therefore ![]() ${\rm sup}\{{\rm Gpd}_R(R/I)|I \text{ is a left ideal}\}\leq n$. On the other hand, by the non-commutative version of [Reference Bennis, Hu and Wang4, Theorem 1.1], we have that
${\rm sup}\{{\rm Gpd}_R(R/I)|I \text{ is a left ideal}\}\leq n$. On the other hand, by the non-commutative version of [Reference Bennis, Hu and Wang4, Theorem 1.1], we have that ![]() ${\rm GPD}(R)={\rm sup}\{{\rm Gpd}_R(R/I)|I \text{ is a left ideal}\}\leq n$. Finally, using Theorem 4.16, we get that
${\rm GPD}(R)={\rm sup}\{{\rm Gpd}_R(R/I)|I \text{ is a left ideal}\}\leq n$. Finally, using Theorem 4.16, we get that ![]() ${\rm PGFD}(R)={\rm GPD}(R)\leq n$ which completes the proof.
${\rm PGFD}(R)={\rm GPD}(R)\leq n$ which completes the proof.
Acknowledgements
The author would like to thank Marco A. Pérez for his kindness in sharing his book [Reference Pérez30] and for informing me about the Corrigendum [Reference Huerta, Mendoza and Pérez27]. Additionally, gratitude is extended to Sergio Estrada for identifying a misprint in the proof of Lemma 4.8 and for sharing the reference [Reference Wang, Yang, Shao and Zhang34]. Special thanks also go to Luis Oyonarte for his comments on an earlier version of this paper and for his constant support. Finally, we express our appreciation to the referee for suggestions that enhanced the exposition.


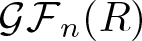
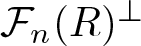

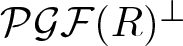

 . The homotopy category of this model structure is triangulated equivalent to the stable category
. The homotopy category of this model structure is triangulated equivalent to the stable category