Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T10:21:15.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed Bruce–Roberts numbers

Part of: Singularities

Published online by Cambridge University Press:  27 February 2020

Carles Bivià-Ausina  and
Maria Aparecida Soares Ruas
Carles Bivià-Ausina
Affiliation:
Institut Universitari de Matemàtica Pura i Aplicada, Universitat Politècnica de València, Camí de Vera, s/n, València 46022, Spain ([email protected])
Maria Aparecida Soares Ruas
Affiliation:
Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, Av. Trabalhador São-carlense, 400, São Carlos, SP13566-590, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the notions of μ*-sequences and Tjurina numbers of functions to the framework of Bruce–Roberts numbers, that is, to pairs formed by the germ at 0 of a complex analytic variety X ⊆ ℂn and a finitely 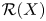${\mathcal R}(X)$-determined analytic function germ f : (ℂn, 0) → (ℂ, 0). We analyze some fundamental properties of these numbers.

Keywords

Milnor numberlogarithmic vector fieldsTjurina numberfinite determinacy

MSC classification

Primary: 32S05: Local singularities
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 2 , May 2020 , pp. 456 - 474
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ahmed, I., Ruas, M. A. S. and Tomazella, J., Invariants of topological relative right equivalences, Math. Proc. Camb. Philos. Soc. 155(2) (2013), 307–315.CrossRefGoogle Scholar
2.Aleksandrov, A. G., Cohomology of a quasi-homogeneous complete intersection, Math. USSR Izv. 26 (1986), 437–477.CrossRefGoogle Scholar
3.Briançon, J. and Maynadier-Gervais, H., Sur le nombre de Milnor d'une singularité semi-quasi-homogène, C. R. Math. Acad. Sci. Paris 334(4) (2002), 317–320.CrossRefGoogle Scholar
4.Bruce, J. W. and Roberts, R. M., Critical points of functions on analytic varieties, Topology 27(1) (1988), 57–90.CrossRefGoogle Scholar
5.Damon, J., Higher multiplicities and almost free divisors and complete intersections, Memoirs of the American Mathematical Society, Volume 123 (American Mathematical Society, Providence, RI, 1996).CrossRefGoogle Scholar
6.Damon, J., On the freeness of equisingular deformations of plane curve singularities, Topology Appl. 118(1–2) (2002), 31–43.CrossRefGoogle Scholar
7.Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H., Singular 4-0-2. A computer algebra system for polynomial computations. Available at http://www.singular.uni-kl.de (2015).Google Scholar
8.Gaffney, T., Multiplicities and equisingularity of icis germs, Invent. Math. 123(1) (1996), 209–220.CrossRefGoogle Scholar
9.De Góes Grulha, N. Jr., The Euler obstruction and Bruce–Roberts' Milnor number, Q. J. Math. 60 (2009), 291–302.CrossRefGoogle Scholar
10.Giusti, M. and Henry, J.-P. G., Minorations de nombres de Milnor, Bull. Soc. Math. France 108(1) (1980), 17–45.CrossRefGoogle Scholar
11.Greuel, G., Der Gauss–Mannin–Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten, Math. Ann. 214 (1975), 235–266.CrossRefGoogle Scholar
12.Hauser, H. and Müller, G., On the Lie algebra T(X) of vector fields on a singularity, J. Math. Sci. Univ. Tokyo 1(1) (1994), 239–250.Google Scholar
13.Hauser, H. and Müller, G., Affine varieties and Lie algebras of vector fields, Manuscripta Math. 80(3) (1993), 309–337.CrossRefGoogle Scholar
14.Huneke, C. and Swanson, I., Integral closure of ideals, rings, and modules, London Mathematical Society Lecture Note Series, Volume 336 (Cambridge, Cambridge University Press, 2006).Google Scholar
15.Liu, Y., Milnor and Tjurina numbers for hypersurface germs with isolated singularity, C. R. Math. Acad. Sci. Paris 356(9) (2018), 963–966.CrossRefGoogle Scholar
16.Looijenga, E. J. N., Isolated singular points on complete intersections, London Mathematical Society Lecture Note Series, Volume 77 (Cambridge, Cambridge University Press, 1984).CrossRefGoogle Scholar
17.Nuño-Ballesteros, J. J., Oréfice, B. and Tomazella, J., The Bruce–Roberts number of a function on a weighted homogeneous hypersurface, Q. J. Math. 64(1) (2013), 269–280.CrossRefGoogle Scholar
18.Ohmoto, T., Suwa, T. and Yokura, S., A remark on the Chern classes of local complete intersections, Proc. Japan Acad. Ser. A Math. Sci. 73(5) (1997), 93–95.CrossRefGoogle Scholar
19.Saito, K., Theory of logarithmic differential forms and logarithmic vector fields, J. Fac. Sci. Univ. Tokyo Sect. 1A Math. 27(5) (1980), 265–291.Google Scholar
20.Teissier, B., Cycles évanescents, sections planes et conditions de Whitney, Singularités à Cargèse (Rencontre Singularités Géom. Anal., Inst. Études Sci., Cargèse, 1972), Astérisque (7–8) (1973), 285–362.Google Scholar
21.Tráng, L. D., Computation of Milnor number of isolated singularity of complete intersection, Funct. Anal. Appl. 8 (1974), 127–131.CrossRefGoogle Scholar
22.Wahl, J., Derivations, automorphisms and deformations of quasihomogeneous singularities, in Singularities, Part 2 (Arcata, CA, 1981), Proceedings of Symposia in Pure Mathematics, Volume 40, pp. 613–624 (American Mathematical Society, Providence, RI, 1983).CrossRefGoogle Scholar