Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-02T16:03:12.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximum-likelihood estimation of the parameters of a four-parameter class of probability distributions

Published online by Cambridge University Press:  20 January 2009

Siegfried H. Lehnigk
Siegfried H. Lehnigk
Affiliation:
Micom, Amsmi-rd-re-op, Redstone Arsenal, AL 35898-5248, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall concern ourselves with the class of continuous, four-parameter, one-sided probability distributions which can be characterized by the probability density function (pdf) class

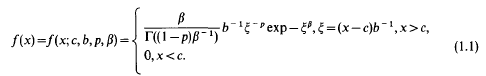
It depends on the four parameters: shift c ∈ R, scale b > 0, initial shape p < 1, and terminal shape β > 0. For p ≦ 0, the definition of f(x) can be completed by setting f(c) = β/bΓ(β−1)>0 if p = 0, and f(c) = 0 if p < 0. For 0 < p < 1, f(x) remains undefined at x = c; f(x)↑ + ∞ as x↓c.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 31 , Issue 2 , June 1988 , pp. 271 - 283
Copyright
Copyright © Edinburgh Mathematical Society 1988

References

REFERENCES

1.Amoroso, L., Richerche intorno alla curva dei reditti, Ann. Mat. Pura. Appl. (4) 2 (1924), 123–157.Google Scholar
2.Courant, R., Differential and Integral Calculus (2nd ed., vol. 1, Interscience Publishers, New York, 1937).Google Scholar
3.Essenwanger, O. M., Applied Statistics in Atmospheric Sciences (Elsevier, Amsterdam, 1976).Google Scholar
4.Gradshteyn, I. S. and Ryzhik, I. M., Tables of Integrals, Series, and Products (4th ed., Academic Press, New York, 1965).Google Scholar
5.Harter, H. L., Maximum-likelihood estimation of the parameters of a four-parameter generalized Gamma population from complete and censored samples, Technometrics 9 (1967), 159–165.CrossRefGoogle Scholar
6.Harter, H. L. and Moore, A. H., Maximum-likelihood estimation of Gamma and Weibull populations from complete and censored samples, Technometrics 7 (1965), 639–643.CrossRefGoogle Scholar
7.Law, A. M. and Kelton, W. D., Simulation Modeling and Analysis (McGraw-Hill, New York, 1982).Google Scholar
8.Lehnigk, S. H., Maxwell and Wien processes as special cases of the generalized Feller diffusion process, J. Math. Phys. 18 (1977), 104–105.CrossRefGoogle Scholar
9.Lehnigk, S. H., Initial condition solutions of the generalized Feller equations, J. Appl. Math. Phys. (ZAMP) 29 (1978), 273–294.Google Scholar
10.Lehnigk, S. H., On a class of probability distributions, Math. Methods Appl. Sci. 9 (1987), 210–219.CrossRefGoogle Scholar
11.Lehnigk, S. H., Characteristic functions of a class of probability distributions, Complex Variables Theory Appl. (1987), to appear.CrossRefGoogle Scholar
12.Van Parr, B. and Webster, J. T., A method for discriminating between failure density functions used in reliability predictions, Technometrics 7 (1965), 1–10.CrossRefGoogle Scholar
13.Roussas, G. G., A First Course in Mathematical Statistics (Addison-Wesley, Reading, 1973).Google Scholar
14.Stacy, E. W., A generalization of the Gamma distribution, Ann. Math. Stat. 33 (1962), 1187–1192.CrossRefGoogle Scholar
15.Stacy, E. W. and Mihram, G. A., Parameter estimation for a generalized Gamma distribution, Technometrics 7 (1965), 349–358.CrossRefGoogle Scholar