Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nordahl, T. E.
and
Scheiblich, H. E.
1978.
Regular * semigroups.
Semigroup Forum,
Vol. 16,
Issue. 1,
p.
369.
Feigenbaum, Ruth
1979.
Regular semigroup congruences.
Semigroup Forum,
Vol. 17,
Issue. 1,
p.
373.
LaTorre, D. R.
1982.
Group congruences on regular semigroups.
Semigroup Forum,
Vol. 24,
Issue. 1,
p.
327.
Krishnam, V. S.
and
Levitan, M.
1986.
Regular involution groupoids-revisited.
Semigroup Forum,
Vol. 35,
Issue. 1,
p.
353.
Blyth, T.S.
and
Almeida Santos, M.H.
1993.
On naturally ordered regular semigroups with biggest idempotents.
Communications in Algebra,
Vol. 21,
Issue. 5,
p.
1761.
Rui, Changxiang
1999.
Weakly regular *-semigroups.
Semigroup Forum,
Vol. 58,
Issue. 3,
p.
463.
Margolis, Stuart
2021.
A tribute to John Meakin on the occasion of his 75th birthday.
Semigroup Forum,
Vol. 102,
Issue. 1,
p.
1.


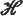 ) of congruences on S which are contained in Green's equivalence
) of congruences on S which are contained in Green's equivalence