Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:23:44.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix Differentiation of the Characteristic Function

Published online by Cambridge University Press:  20 January 2009

H. W. Turnbull
H. W. Turnbull
Affiliation:
St Andrews University.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following work is a sequel to three previous communications, and more particularly to the first. The present object is to shew the effect of repeated operation with the matrix differential operator 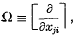, when it acts upon a scalar matrix formed from an n rowed determinant |xij|, or sums of principal minors, the n2 elements xij being treated as independent variables. Thus when z is a scalar quantity ω z means the matrix [∂z/∂xij], whose ijth element is the derivative.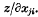

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 2 , Issue 4 , June 1931 , pp. 256 - 264
Copyright
Copyright © Edinburgh Mathematical Society 1931

References

page 256 note 1 I. Turnbull, H. W, On differentiating a matrix, Proc. Edinburgh Math. Soc. (2), 1 (1927), 111–128.CrossRefGoogle Scholar

II. A matrix form of Taylor's Theorem (2), 2 (1929), 33–54.Google Scholar

III. The invariant theory of bilinear forms, Proc. London Math. Soc. (1931).Google Scholar

page 259 note 1 CfDickson, L. E, Modern Algebraic Theories (Chicago, 1926), 48, after replacing P r by C n-l-r.Google Scholar