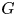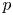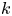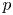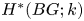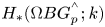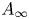1. Introduction
The general context is that we have a finite group $G$![]() , and a field $k$
, and a field $k$![]() of characteristic $p$
of characteristic $p$![]() . We are interested in the differential graded cochain algebra $C^{*}(BG;k)$
. We are interested in the differential graded cochain algebra $C^{*}(BG;k)$![]() and the differential graded algebra $C_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$
and the differential graded algebra $C_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$![]() of chains on the loop space: these two are Koszul dual to each other, and the Eilenberg–Moore and Rothenberg–Steenrod spectral sequences relate the cohomology ring $H^{*}(BG;k)$
of chains on the loop space: these two are Koszul dual to each other, and the Eilenberg–Moore and Rothenberg–Steenrod spectral sequences relate the cohomology ring $H^{*}(BG;k)$![]() to the homology ring $H_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$
to the homology ring $H_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$![]() , see § 5. Of course if $G$
, see § 5. Of course if $G$![]() is a $p$
is a $p$![]() -group, $BG$
-group, $BG$![]() is $p$
is $p$![]() -complete so $\Omega (BG{{}^{{}^{\wedge }}_p})\simeq G$
-complete so $\Omega (BG{{}^{{}^{\wedge }}_p})\simeq G$![]() , but, in general, $H_*(\Omega (BG{{}^{{}^{\wedge }}_p}); k)$
, but, in general, $H_*(\Omega (BG{{}^{{}^{\wedge }}_p}); k)$![]() is infinite dimensional. Henceforth, we will omit the brackets from $\Omega (BG{{}^{{}^{\wedge }}_p})$
is infinite dimensional. Henceforth, we will omit the brackets from $\Omega (BG{{}^{{}^{\wedge }}_p})$![]() .
.
We consider a simple case where the two rings are not formal, but we can identify the $A_{\infty }$![]() structures precisely (see § 3 for a brief summary on $A_{\infty }$
structures precisely (see § 3 for a brief summary on $A_{\infty }$![]() -algebras). From now on, we suppose specifically that $G$
-algebras). From now on, we suppose specifically that $G$![]() is a finite group with cyclic Sylow $p$
is a finite group with cyclic Sylow $p$![]() -subgroup $P$
-subgroup $P$![]() , and let $BG$
, and let $BG$![]() be its classifying space. Then the inclusion of the Sylow $p$
be its classifying space. Then the inclusion of the Sylow $p$![]() -normaliser $N_G(P) \to G$
-normaliser $N_G(P) \to G$![]() and the quotient map $N_G(P) \to N_G(P)/O_{p'}N_G(P)$
and the quotient map $N_G(P) \to N_G(P)/O_{p'}N_G(P)$![]() induce mod $p$
induce mod $p$![]() cohomology equivalences
cohomology equivalences
see Swan [Reference Swan15] or Theorem II.6.8 of Adem and Milgram [Reference Adem and Milgram1]. Hence, after $p$![]() -completion, we have homotopy equivalences
-completion, we have homotopy equivalences
see Lemma I.5.5 of Bousfield and Kan [Reference Bousfield and Kan3]. Here, $O_{p'}N_G(P)$![]() denotes the largest normal $p'$
denotes the largest normal $p'$![]() -subgroup of $N_G(P)$
-subgroup of $N_G(P)$![]() . Thus, $N_G(P)/O_{p'}N_G(P)$
. Thus, $N_G(P)/O_{p'}N_G(P)$![]() is a semidirect product $\mathbb {Z}/p^{n}\rtimes \mathbb {Z}/q$
is a semidirect product $\mathbb {Z}/p^{n}\rtimes \mathbb {Z}/q$![]() , where $q$
, where $q$![]() is a divisor of $p-1$
is a divisor of $p-1$![]() , and $\mathbb {Z}/q$
, and $\mathbb {Z}/q$![]() acts faithfully as a group of automorphisms of $\mathbb {Z}/p^{n}$
acts faithfully as a group of automorphisms of $\mathbb {Z}/p^{n}$![]() . In particular, the isomorphism type of $N_G(P)/O_{p'}N_G(P)$
. In particular, the isomorphism type of $N_G(P)/O_{p'}N_G(P)$![]() only depends on $|P|=p^{n}$
only depends on $|P|=p^{n}$![]() and the inertial index $q=|N_G(P):C_G(P)|$
and the inertial index $q=|N_G(P):C_G(P)|$![]() , and therefore so does the homotopy type of $BG{{}^{{}^{\wedge }}_p}$
, and therefore so does the homotopy type of $BG{{}^{{}^{\wedge }}_p}$![]() . Our main theorem determines the multiplication maps $m_i$
. Our main theorem determines the multiplication maps $m_i$![]() in the $A_\infty$
in the $A_\infty$![]() structure on $H^{*}(BG;k)$
structure on $H^{*}(BG;k)$![]() and $H_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$
and $H_*(\Omega (BG{{}^{{}^{\wedge }}_p});k)$![]() arising from $C^{*}(BG;k)$
arising from $C^{*}(BG;k)$![]() and $C_*(\Omega (BG{{}^{{}^{\wedge }}_p}); k)$
and $C_*(\Omega (BG{{}^{{}^{\wedge }}_p}); k)$![]() respectively. We will suppose from now on that $p^{n}>2,\, q>1$
respectively. We will suppose from now on that $p^{n}>2,\, q>1$![]() since the case of a $p$
since the case of a $p$![]() -group is well understood.
-group is well understood.
The starting point is the cohomology ring
There is a preferred generator $t_1\in H^{1}(B\mathbb {Z}/p^{n};k)=\mathrm {Hom}(\mathbb {Z}/p^{n},\,k)$![]() and we take $x_1\in H^{2}(B\mathbb {Z}/p^{n};k)$
and we take $x_1\in H^{2}(B\mathbb {Z}/p^{n};k)$![]() to be the $n$
to be the $n$![]() th Bockstein of $t_1$
th Bockstein of $t_1$![]() . Now take $x=x_1^{q},\, t=x_1^{q-1}t_1$
. Now take $x=x_1^{q},\, t=x_1^{q-1}t_1$![]() .
.
Before stating our result, we should be clear about grading and signs.
Remark 1.1 We will be discussing both homology and cohomology, so we should be explicit that everything is graded homologically, so that differentials always lower degree. Explicitly, the degree of an element of $H^{i}(G;k)$![]() is $-i$
is $-i$![]() .
.
Remark 1.2 Sign conventions for Massey products and $A_{\infty }$![]() algebras mean that a specific sign will enter repeatedly in our statements, so for brevity, we write
algebras mean that a specific sign will enter repeatedly in our statements, so for brevity, we write

Theorem 1.3 Let $G$![]() be a finite group with cyclic Sylow $p$
be a finite group with cyclic Sylow $p$![]() -subgroup $P$
-subgroup $P$![]() of order $p^{n}$
of order $p^{n}$![]() and inertial index $q$
and inertial index $q$![]() so that
so that
Up to quasi-isomorphism, the $A_\infty$![]() structure on $H^{*}(BG;k)$
structure on $H^{*}(BG;k)$![]() is determined by
is determined by
where $h=p^{n}-(p^{n}-1)/q$![]() . This implies
. This implies
for all $j_1,\, \ldots ,\, j_{p^{n}}\geq 0$![]() . All $m_i$
. All $m_i$![]() for $i>2$
for $i>2$![]() on all other $i$
on all other $i$![]() -tuples of monomials give zero.
-tuples of monomials give zero.
If $q>1$![]() and $p^{n}\ne 3$
and $p^{n}\ne 3$![]() then
then
Up to quasi-isomorphism, the $A_\infty$![]() structure is determined by
structure is determined by
This implies
for all $j_1,\, \ldots ,\, j_{p^{n}}\geq 0$![]() . All $m_i$
. All $m_i$![]() for $i>2$
for $i>2$![]() on all other $i$
on all other $i$![]() -tuples of monomials give zero.
-tuples of monomials give zero.
If $q>1$![]() and $p^{n}=3$
and $p^{n}=3$![]() then $q=2$
then $q=2$![]() and
and
and all $m_i$![]() are zero for $i>2$
are zero for $i>2$![]() .
.
2. The group algebra and its cohomology
We assume from now on, without loss of generality, that $G$![]() has a normal cyclic Sylow $p$
has a normal cyclic Sylow $p$![]() -subgroup $P=C_G(P)$
-subgroup $P=C_G(P)$![]() , with inertial index $q=|G:P|$
, with inertial index $q=|G:P|$![]() . We shall assume that $q>1$
. We shall assume that $q>1$![]() , which then forces $p$
, which then forces $p$![]() to be odd. For notation, let
to be odd. For notation, let
where $\gamma$![]() is a primitive $q$
is a primitive $q$![]() th root of unity modulo $p^{n}$
th root of unity modulo $p^{n}$![]() . Let $P=\langle g\rangle$
. Let $P=\langle g\rangle$![]() and $H=\langle s\rangle$
and $H=\langle s\rangle$![]() as subgroups of $G$
as subgroups of $G$![]() .
.
In this section, we introduce a grading on $kG$![]() . This comes from the fact that the radical filtration of $kG$
. This comes from the fact that the radical filtration of $kG$![]() is isomorphic to its associated graded in this case. This is a somewhat rare phenomenon, but when it happens, it induces an extra grading on mod $p$
is isomorphic to its associated graded in this case. This is a somewhat rare phenomenon, but when it happens, it induces an extra grading on mod $p$![]() cohomology of $BG$
cohomology of $BG$![]() and homology of $\Omega BG{{}^{{}^{\wedge }}_p}$
and homology of $\Omega BG{{}^{{}^{\wedge }}_p}$![]() , that we can exploit to good effect.
, that we can exploit to good effect.
Let $k$![]() be a field of characteristic $p$
be a field of characteristic $p$![]() . The action of $H$
. The action of $H$![]() on $kP$
on $kP$![]() by conjugation preserves the radical series, and since $|H|$
by conjugation preserves the radical series, and since $|H|$![]() is not divisible by $p$
is not divisible by $p$![]() , there are invariant complements. Thus, we may choose an element $U\in J(kP)$
, there are invariant complements. Thus, we may choose an element $U\in J(kP)$![]() such that $U$
such that $U$![]() spans an $H$
spans an $H$![]() -invariant complement of $J^{2}(kP)$
-invariant complement of $J^{2}(kP)$![]() in $J(kP)$
in $J(kP)$![]() . It can be checked that
. It can be checked that

is such an element, and that $sUs^{-1}=\gamma U$![]() . This gives us the following presentation for $kG$
. This gives us the following presentation for $kG$![]() :
:
We shall regard $kG$![]() as a $\mathbb {Z}[{1}/{q}]$
as a $\mathbb {Z}[{1}/{q}]$![]() -graded algebra with $|s|=0$
-graded algebra with $|s|=0$![]() and $|U|=1/q$
and $|U|=1/q$![]() . Then the bar resolution is doubly graded, and taking homomorphisms into $k$
. Then the bar resolution is doubly graded, and taking homomorphisms into $k$![]() , the cochains $C^{*}(BG;k)$
, the cochains $C^{*}(BG;k)$![]() inherit a double grading. The differential decreases the homological grading and preserves the internal grading. Thus, the cohomology $H^{*}(G,\,k)=H^{*}(BG;k)$
inherit a double grading. The differential decreases the homological grading and preserves the internal grading. Thus, the cohomology $H^{*}(G,\,k)=H^{*}(BG;k)$![]() is doubly graded:
is doubly graded:
where $|x|=(-2q,\,-p^{n})$![]() , $|t|=(-2q+1,\,-h)$
, $|t|=(-2q+1,\,-h)$![]() , and $h=p^{n}-(p^{n}-1)/q$
, and $h=p^{n}-(p^{n}-1)/q$![]() . Here, the first degree is homological, the second internal. The Massey product $\langle t,\,t,\,\ldots ,\,t\rangle$
. Here, the first degree is homological, the second internal. The Massey product $\langle t,\,t,\,\ldots ,\,t\rangle$![]() ($p^{n}$
($p^{n}$![]() repetitions) is equal to $-x^{h}$
repetitions) is equal to $-x^{h}$![]() . This may easily be determined by restriction to $P$
. This may easily be determined by restriction to $P$![]() , where it is well known that the $p^{n}$
, where it is well known that the $p^{n}$![]() -fold Massey product of the degree one exterior generator is a non-zero degree two element. The usual convention is to make the constant $-1$
-fold Massey product of the degree one exterior generator is a non-zero degree two element. The usual convention is to make the constant $-1$![]() , because this Massey product is minus the $n$
, because this Massey product is minus the $n$![]() th Bockstein of $t$
th Bockstein of $t$![]() [Reference Kraines10, Theorem 19].
[Reference Kraines10, Theorem 19].
3. $A_\infty$ -algebras
-algebras
An $A_{\infty }$![]() -algebra over a field is a $\mathbb {Z}$
-algebra over a field is a $\mathbb {Z}$![]() -graded vector space $A$
-graded vector space $A$![]() with graded maps $m_n: A^{\otimes n}\rightarrow A$
with graded maps $m_n: A^{\otimes n}\rightarrow A$![]() of degree $n-2$
of degree $n-2$![]() for $n\geq 1$
for $n\geq 1$![]() satisfying
satisfying
for $n\geq 1$![]() . The map $m_1$
. The map $m_1$![]() is therefore a differential, and the map $m_2$
is therefore a differential, and the map $m_2$![]() induces a product on $H_*(A)$
induces a product on $H_*(A)$![]() .
.
A theorem of Kadeishvili [Reference Kadeishvili7] (see also Keller [Reference Keller8, Reference Keller9] or Merkulov [Reference Merkulov13]) may be stated as follows. Suppose that we are given a differential graded algebra $A$![]() , over a field $k$
, over a field $k$![]() . Let $Z^{*}(A)$
. Let $Z^{*}(A)$![]() be the cocycles, $B^{*}(A)$
be the cocycles, $B^{*}(A)$![]() be the coboundaries, and $H^{*}(A)=Z^{*}(A)/B^{*}(A)$
be the coboundaries, and $H^{*}(A)=Z^{*}(A)/B^{*}(A)$![]() . Choose a vector space splitting $f_1\colon H^{*}(A) \to Z^{*}(A) \subseteq A$
. Choose a vector space splitting $f_1\colon H^{*}(A) \to Z^{*}(A) \subseteq A$![]() of the quotient. Then this gives by an inductive procedure an $A_\infty$
of the quotient. Then this gives by an inductive procedure an $A_\infty$![]() structure on $H^{*}(A)$
structure on $H^{*}(A)$![]() so that the map $f_1$
so that the map $f_1$![]() is the degree one part of a quasi-isomorphism of $A_\infty$
is the degree one part of a quasi-isomorphism of $A_\infty$![]() -algebras.
-algebras.
If $A$![]() happens to carry auxiliary gradings respected by the product structure and preserved by the differential, then it is easy to check from the inductive procedure that the maps in the construction may be chosen so that they also respect these gradings. It then follows that the structure maps $m_i$
happens to carry auxiliary gradings respected by the product structure and preserved by the differential, then it is easy to check from the inductive procedure that the maps in the construction may be chosen so that they also respect these gradings. It then follows that the structure maps $m_i$![]() of the $A_\infty$
of the $A_\infty$![]() structure on $H^{*}(A)$
structure on $H^{*}(A)$![]() also respect these gradings.
also respect these gradings.
Let us apply this to $H^{*}(BG;k)$![]() . We examine the elements $m_i(t,\,\ldots ,\,t)$
. We examine the elements $m_i(t,\,\ldots ,\,t)$![]() . By definition, we have $m_1(t)=0$
. By definition, we have $m_1(t)=0$![]() and $m_2(t,\,t)=0$
and $m_2(t,\,t)=0$![]() . The degree of $m_i(t,\,\ldots ,\,t)$
. The degree of $m_i(t,\,\ldots ,\,t)$![]() is $i$
is $i$![]() times the degree of $t$
times the degree of $t$![]() , increased in the homological direction by $i-2$
, increased in the homological direction by $i-2$![]() . This gives
. This gives
The homological degree is even, so if $m_i(t,\, \ldots ,\, t)$![]() is non-zero then it is a multiple of a power of $x$
is non-zero then it is a multiple of a power of $x$![]() . Comparing degrees, if $m_i(t,\,\ldots ,\,t)$
. Comparing degrees, if $m_i(t,\,\ldots ,\,t)$![]() is a non-zero multiple of $x^{\alpha }$
is a non-zero multiple of $x^{\alpha }$![]() then we have
then we have
Eliminating $\alpha$![]() , we obtain $(iq-i+1)p^{n}=ihq$
, we obtain $(iq-i+1)p^{n}=ihq$![]() . Substituting $h=p^{n}-(p^{n}-1)/q$
. Substituting $h=p^{n}-(p^{n}-1)/q$![]() , this gives $i=p^{n}$
, this gives $i=p^{n}$![]() . Finally, since the Massey product of $p^{n}$
. Finally, since the Massey product of $p^{n}$![]() copies of $t$
copies of $t$![]() is equal to $-x^{h}$
is equal to $-x^{h}$![]() , it follows that $m_{p^{n}}(t,\,\ldots ,\,t)=\epsilon (p^{n}) x^{h}$
, it follows that $m_{p^{n}}(t,\,\ldots ,\,t)=\epsilon (p^{n}) x^{h}$![]() , where the sign is as defined in Remark 1.2 ([Reference Lu, Palmieri, Wu and Zhang11, Theorem 3.1], corrected in [Reference Buijs, Moreno-Fernández and Murillo4, Theorem 3.2]). Thus, we have
, where the sign is as defined in Remark 1.2 ([Reference Lu, Palmieri, Wu and Zhang11, Theorem 3.1], corrected in [Reference Buijs, Moreno-Fernández and Murillo4, Theorem 3.2]). Thus, we have

We shall elaborate on this argument in a more general context in the next section, where we shall see that the rest of the $A_\infty$![]() structure is also determined in a similar way.
structure is also determined in a similar way.
4. $A_\infty$ structures on a polynomial tensor exterior algebra
structures on a polynomial tensor exterior algebra
In this section, we shall examine the following general situation. Our goal is to establish that there are only two possible $A_\infty$![]() structures satisfying Hypothesis 4.1, and that the Koszul dual also satisfies the same hypothesis with the roles of $a$
structures satisfying Hypothesis 4.1, and that the Koszul dual also satisfies the same hypothesis with the roles of $a$![]() and $b$
and $b$![]() , and of $h$
, and of $h$![]() and $\ell$
and $\ell$![]() reversed.
reversed.
Hypothesis 4.1 $A$![]() is a $\mathbb {Z}\times \mathbb {Z}$
is a $\mathbb {Z}\times \mathbb {Z}$![]() -graded $A_\infty$
-graded $A_\infty$![]() -algebra over a field $k$
-algebra over a field $k$![]() , where the operators $m_i$
, where the operators $m_i$![]() have degree $(i-2,\,0)$
have degree $(i-2,\,0)$![]() , satisfying
, satisfying
(1) $m_1=0$
 , so that $m_2$
, so that $m_2$ is strictly associative,
is strictly associative,(2) ignoring the $m_i$
 with $i>2$
with $i>2$ , the algebra $A$
, the algebra $A$ is $k[x] \otimes \Lambda (t)$
is $k[x] \otimes \Lambda (t)$ where $|x|=(-2a,\,-\ell )$
where $|x|=(-2a,\,-\ell )$ and $|t|=(-2b-1,\,-h)$
and $|t|=(-2b-1,\,-h)$ , and
, and(3) $ha-\ell b = 1$
 .
.
Remarks 4.2
(i) The $A_\infty$
 -algebra $H^{*}(BG;k)$
-algebra $H^{*}(BG;k)$ of the last section satisfies this hypothesis, with $a=q$
of the last section satisfies this hypothesis, with $a=q$ , $b=q-1$
, $b=q-1$ , $h=p^{n}-(p^{n}-1)/q$
, $h=p^{n}-(p^{n}-1)/q$ , $\ell =p^{n}$
, $\ell =p^{n}$ .
.(ii) By comparing degrees, if we have $m_\ell (t,\,\ldots ,\,t)=\epsilon (\ell ) x^{h}$
 then
then
$(2b+1)\ell + 2-\ell = 2ah$![]() and so $ha-\ell b = 1$
and so $ha-\ell b = 1$![]() . This explains the role of part (3) of the hypothesis. The consequence is, of course, that $a$
. This explains the role of part (3) of the hypothesis. The consequence is, of course, that $a$![]() and $b$
and $b$![]() are coprime, and so are $h$
are coprime, and so are $h$![]() and $\ell$
and $\ell$![]() .
.
Lemma 4.3 If $m_i(t,\,\ldots ,\,t)$![]() is non-zero, then $i=\ell > 2$
is non-zero, then $i=\ell > 2$![]() and $m_\ell (t,\,\ldots ,\,t)$
and $m_\ell (t,\,\ldots ,\,t)$![]() is a multiple of $x^{h}$
is a multiple of $x^{h}$![]() .
.
Proof. The argument is the same as in the last section. The degree of $m_i(t,\,\ldots ,\,t)$![]() is $i|t| +(i- 2,\,0) = (-2ib - 2,\, -ih)$
is $i|t| +(i- 2,\,0) = (-2ib - 2,\, -ih)$![]() . Since the homological degree is even, if $m_i(t,\,\ldots ,\,t)$
. Since the homological degree is even, if $m_i(t,\,\ldots ,\,t)$![]() is non-zero then it is a multiple of some power of $x$
is non-zero then it is a multiple of some power of $x$![]() , say $x^{\alpha }$
, say $x^{\alpha }$![]() . Then we have
. Then we have
Eliminating $\alpha$![]() gives $(ib+1)\ell =iha$
gives $(ib+1)\ell =iha$![]() , and so using $ha-\ell b =1$
, and so using $ha-\ell b =1$![]() we have $i=\ell$
we have $i=\ell$![]() . Substituting back gives $\alpha = h$
. Substituting back gives $\alpha = h$![]() .
.
Elaborating on this argument gives the entire $A_\infty$![]() structure. If $m_\ell (t,\,\ldots ,\,t)$
structure. If $m_\ell (t,\,\ldots ,\,t)$![]() is non-zero, then by rescaling the variables $t$
is non-zero, then by rescaling the variables $t$![]() and $x$
and $x$![]() if necessary we can assume that $m_\ell (t,\,\ldots ,\,t)=\epsilon (\ell ) x^{h}$
if necessary we can assume that $m_\ell (t,\,\ldots ,\,t)=\epsilon (\ell ) x^{h}$![]() (note that we can even do this without extending the field, since $\ell$
(note that we can even do this without extending the field, since $\ell$![]() and $h$
and $h$![]() are coprime).
are coprime).
Proposition 4.4 If $m_\ell (t,\,\ldots ,\,t)=0$![]() then all $m_i$
then all $m_i$![]() are zero for $i>2$
are zero for $i>2$![]() . If $m_\ell (t,\,\ldots ,\,t)= \epsilon (\ell ) x^{h}$
. If $m_\ell (t,\,\ldots ,\,t)= \epsilon (\ell ) x^{h}$![]() then $m_\ell (x^{j_1}t,\,\ldots ,\,x^{j_\ell }t)= \epsilon (\ell )x^{h+j_1+\cdots +j_\ell }$
then $m_\ell (x^{j_1}t,\,\ldots ,\,x^{j_\ell }t)= \epsilon (\ell )x^{h+j_1+\cdots +j_\ell }$![]() , and all $m_i$
, and all $m_i$![]() for $i>2$
for $i>2$![]() on all other $i$
on all other $i$![]() -tuples of monomials give zero.
-tuples of monomials give zero.
Proof. All monomials live in different degrees, so we do not need to consider linear combinations of monomials. Suppose that $m_i(x^{j_1}t^{\varepsilon _1},\,\ldots ,\,x^{j_i}t^{\varepsilon _i})$![]() is some constant multiple of $x^{j}t^{\varepsilon }$
is some constant multiple of $x^{j}t^{\varepsilon }$![]() , where each of $\varepsilon _1,\,\ldots ,\,\varepsilon _i,\,\varepsilon$
, where each of $\varepsilon _1,\,\ldots ,\,\varepsilon _i,\,\varepsilon$![]() is either zero or one. Then comparing degrees, we have
is either zero or one. Then comparing degrees, we have
Setting
we have $\beta \leqslant i$![]() , and
, and
Thus
Eliminating $\alpha$![]() , we obtain
, we obtain
Since $ha-\ell b=1$![]() , this gives $\beta = \ell (i-2) /(\ell -2)$
, this gives $\beta = \ell (i-2) /(\ell -2)$![]() . Combining this with $\beta \leqslant i$
. Combining this with $\beta \leqslant i$![]() gives $i\leqslant \ell$
gives $i\leqslant \ell$![]() . If $i<\ell$
. If $i<\ell$![]() then $\beta$
then $\beta$![]() is not divisible by $\ell$
is not divisible by $\ell$![]() , and so $\alpha \ell + \beta h = 0$
, and so $\alpha \ell + \beta h = 0$![]() cannot hold. So we have $\beta =i=\ell$
cannot hold. So we have $\beta =i=\ell$![]() , $\varepsilon _1=\dots =\varepsilon _\ell =1$
, $\varepsilon _1=\dots =\varepsilon _\ell =1$![]() , $\varepsilon =0$
, $\varepsilon =0$![]() , $\alpha =-h$
, $\alpha =-h$![]() , and $j=h+j_1+\cdots +j_\ell$
, and $j=h+j_1+\cdots +j_\ell$![]() . Finally, the identities satisfied by the $m_i$
. Finally, the identities satisfied by the $m_i$![]() for an $A_\infty$
for an $A_\infty$![]() structure show that all the constant multiples have to be the same, hence all equal to zero or after rescaling, all equal to $\epsilon (\ell )$
structure show that all the constant multiples have to be the same, hence all equal to zero or after rescaling, all equal to $\epsilon (\ell )$![]() .
.
Theorem 4.5 Under Hypothesis 4.1, if $\ell > 2$![]() then there are two possible $A_\infty$
then there are two possible $A_\infty$![]() structures on $A$
structures on $A$![]() . There is the formal one, where $m_i$
. There is the formal one, where $m_i$![]() is equal to zero for $i>2$
is equal to zero for $i>2$![]() , and the non-formal one, where after replacing $x$
, and the non-formal one, where after replacing $x$![]() and $t$
and $t$![]() by suitable multiples, the only non-zero $m_i$
by suitable multiples, the only non-zero $m_i$![]() with $i>2$
with $i>2$![]() is $m_\ell$
is $m_\ell$![]() , and the only non-zero values on monomials are given by
, and the only non-zero values on monomials are given by
Theorem 4.6 Let $G=\mathbb {Z}/p^{n} \rtimes \mathbb {Z}/q$![]() as above, and $k$
as above, and $k$![]() a field of characteristic $p$
a field of characteristic $p$![]() . Then the $A_\infty$
. Then the $A_\infty$![]() structure on $H^{*}(G,\,k)$
structure on $H^{*}(G,\,k)$![]() given by Kadeishvili's theorem may be taken to be the non-formal possibility named in the above theorem, with $a=q$
given by Kadeishvili's theorem may be taken to be the non-formal possibility named in the above theorem, with $a=q$![]() , $b=q-1$
, $b=q-1$![]() , $h=p^{n}-(p^{n}-1)/q$
, $h=p^{n}-(p^{n}-1)/q$![]() , $\ell =p^{n}$
, $\ell =p^{n}$![]() .
.
Proof. Since we have $m_{p^{n}}(t,\,\ldots ,\,t)=\epsilon (p^{n}) x^{h}$![]() , the formal possibility does not hold.
, the formal possibility does not hold.
Remark 4.7 Dag Madsen's thesis [Reference Madsen12] has an appendix in which the $A_\infty$![]() structure is computed for the cohomology of a truncated polynomial ring, reaching similar conclusions by more direct methods. A similar computation appears in Examples 7.1.5 and 7.2.4 of the book by Witherspoon [Reference Witherspoon16].
structure is computed for the cohomology of a truncated polynomial ring, reaching similar conclusions by more direct methods. A similar computation appears in Examples 7.1.5 and 7.2.4 of the book by Witherspoon [Reference Witherspoon16].
5. Loops on $BG{{}^{{}^{\wedge }}_p}$
In general, for a finite group $G$![]() , the classifying space $BG$
, the classifying space $BG$![]() is $p$
is $p$![]() -good, see Proposition VII.5.1 of Bousfield and Kan [Reference Bousfield and Kan3]. So its $p$
-good, see Proposition VII.5.1 of Bousfield and Kan [Reference Bousfield and Kan3]. So its $p$![]() -completion $BG{{}^{{}^{\wedge }}_p}$
-completion $BG{{}^{{}^{\wedge }}_p}$![]() is $p$
is $p$![]() -complete. This space and its loop space have been the subject of considerable study, beginning with the work of Cohen and Levi [Reference Cohen and Levi5]. We have $H^{*}(BG{{}^{{}^{\wedge }}_p};k)\cong H^{*}(BG;k)=H^{*}(G,\,k)$
-complete. This space and its loop space have been the subject of considerable study, beginning with the work of Cohen and Levi [Reference Cohen and Levi5]. We have $H^{*}(BG{{}^{{}^{\wedge }}_p};k)\cong H^{*}(BG;k)=H^{*}(G,\,k)$![]() and $\pi _1(BG{{}^{{}^{\wedge }}_p})=G/O^{p}(G)$
and $\pi _1(BG{{}^{{}^{\wedge }}_p})=G/O^{p}(G)$![]() , the largest $p$
, the largest $p$![]() -quotient of $G$
-quotient of $G$![]() . In our case, $G=\mathbb {Z}/p^{n}\rtimes \mathbb {Z}/q$
. In our case, $G=\mathbb {Z}/p^{n}\rtimes \mathbb {Z}/q$![]() with $q>1$
with $q>1$![]() , we have $G=O^{p}(G)$
, we have $G=O^{p}(G)$![]() and so $BG{{}^{{}^{\wedge }}_p}$
and so $BG{{}^{{}^{\wedge }}_p}$![]() is simply connected. So the Eilenberg–Moore spectral sequence converges to the homology of its loop space:
is simply connected. So the Eilenberg–Moore spectral sequence converges to the homology of its loop space:
(Eilenberg–Moore [Reference Eilenberg and Moore6], Smith [Reference Smith14]). The internal grading on $C^{*}(BG;k)$![]() gives this spectral sequence a third grading that is preserved by the differentials, and $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)$
gives this spectral sequence a third grading that is preserved by the differentials, and $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)$![]() is again doubly graded. Since $H^{*}(G,\,k)=k[x] \otimes \Lambda (t)$
is again doubly graded. Since $H^{*}(G,\,k)=k[x] \otimes \Lambda (t)$![]() with $|x|=(-2q,\,-p^{n})$
with $|x|=(-2q,\,-p^{n})$![]() and $|t|=(-2q+1,\,-h)$
and $|t|=(-2q+1,\,-h)$![]() , it follows that the $E^{2}$
, it follows that the $E^{2}$![]() page of this spectral sequence is $k[\tau ] \otimes \Lambda (\xi )$
page of this spectral sequence is $k[\tau ] \otimes \Lambda (\xi )$![]() where $|\xi |=(-1,\,2q,\,p^{n})$
where $|\xi |=(-1,\,2q,\,p^{n})$![]() and $|\tau |=(-1,\,2q-1,\,h)$
and $|\tau |=(-1,\,2q-1,\,h)$![]() (recall $h=p^{n}-(p^{n}-1)/q$
(recall $h=p^{n}-(p^{n}-1)/q$![]() ). Provided that we are not in the case $h=2$
). Provided that we are not in the case $h=2$![]() , which only happens if $p^{n}=3$
, which only happens if $p^{n}=3$![]() , ungrading $E^{\infty }$
, ungrading $E^{\infty }$![]() gives
gives
with $|\tau |=(2q-2,\,h)$![]() and $|\xi |=(2q-1,\,p^{n})$
and $|\xi |=(2q-1,\,p^{n})$![]() .
.
In the exceptional case $h=2$![]() , $p^{n}=3$
, $p^{n}=3$![]() , we have $q=2$
, we have $q=2$![]() , and the group $G$
, and the group $G$![]() is the symmetric group $\Sigma _3$
is the symmetric group $\Sigma _3$![]() of degree three. An explicit computation (for example by squeezed resolutions [Reference Benson2]) gives
of degree three. An explicit computation (for example by squeezed resolutions [Reference Benson2]) gives
with $|\tau |=(2,\,2)$![]() and $|\xi |=(3,\,3)$
and $|\xi |=(3,\,3)$![]() , and the two gradings collapse to a single grading.
, and the two gradings collapse to a single grading.
Applying Theorem 4.5, and using the fact that either formal case is Koszul dual to the other, we have the following.
Theorem 5.1 Suppose that $p^{n}\ne 3$![]() . Then the $A_\infty$
. Then the $A_\infty$![]() structure on $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)=k[\tau ]\otimes \Lambda (\xi )$
structure on $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)=k[\tau ]\otimes \Lambda (\xi )$![]() is given by
is given by
and for $i>2$![]() , all $m_i$
, all $m_i$![]() on all other $i$
on all other $i$![]() -tuples of monomials give zero.
-tuples of monomials give zero.
Again using [Reference Lu, Palmieri, Wu and Zhang11] corrected in [Reference Buijs, Moreno-Fernández and Murillo4], we may reinterpret this in terms of Massey products.
Corollary 5.2 In $H_*(\Omega BG{{}^{{}^{\wedge }}_p};k)$![]() , the Massey products $\langle \xi ,\,\ldots ,\,\xi \rangle$
, the Massey products $\langle \xi ,\,\ldots ,\,\xi \rangle$![]() ($i$
($i$![]() times) vanish for $0< i< h$
times) vanish for $0< i< h$![]() , and give $-\tau ^{p^{n}}$
, and give $-\tau ^{p^{n}}$![]() for $i=h$
for $i=h$![]() .
.
Note that the exceptional case $p^{n}=3$![]() also fits the corollary, if we interpret a $2$
also fits the corollary, if we interpret a $2$![]() -fold Massey product as an ordinary product.
-fold Massey product as an ordinary product.
Acknowledgements
The authors are grateful to EPSRC: the second author is supported by EP/P031080/1, which also enabled the first author to visit Warwick. The authors would also like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for providing an opportunity to work on this project during the simultaneous programmes ‘$K$![]() -theory, algebraic cycles and motivic homotopy theory’ and ‘Groups, representations and applications: new perspectives’ (one author was supported by each programme).
-theory, algebraic cycles and motivic homotopy theory’ and ‘Groups, representations and applications: new perspectives’ (one author was supported by each programme).