Hostname: page-component-f554764f5-wjqwx Total loading time: 0 Render date: 2025-04-11T19:07:05.776Z Has data issue: false hasContentIssue false
  • English
  • Français

A logarithmic uncertainty principle for functions with radial symmetry

Part of: Normed linear spaces and Banach spaces; Banach lattices Linear function spaces and their duals

Published online by Cambridge University Press:  31 March 2025

Jacopo Bellazzini Open the ORCID record for Jacopo Bellazzini [Opens in a new window]  and
Matteo Nesi Open the ORCID record for Matteo Nesi [Opens in a new window]
Jacopo Bellazzini
Affiliation:
Dipartimento di Matematica, Università di Pisa, Largo B. Pontecorvo 5, Pisa, Italy ([email protected])
Matteo Nesi
Affiliation:
Departement Mathematik und Informatik, Universität Basel, Spiegelgasse 1, Basel, Switzerland
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove a new uncertainty principle for functions with radial symmetry by differentiating a radial version of the Stein–Weiss inequality. The difficulty is to prove the differentiability in the limit of the best constant that unlike the general case it is not known. We provide also an integral alternative formula for the logarithmic weight 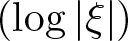$(\log|\xi|)$ in Fourier domain.

Keywords

logarithmic uncertaintyStein–Weiss inequalityfractional Sobolev spaces

MSC classification

Primary: 39B62: Functional inequalities, including subadditivity, convexity, etc. 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems 46B70: Interpolation between normed linear spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 14
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bahouri, H., Chemin, J. Y. and Danchin, R., Fourier Analysis and Nonlinear Partial Differential Equations. Grundlehren der Mathematischen Wissenschaften (Springer, Berlin Heidelberg, 2011).CrossRefGoogle Scholar
Beckner, W., Inequalities in Fourier analysis, Ann. Math. 102 (1975), 159–182.CrossRefGoogle Scholar
Beckner, W., Pitt’s inequality and the uncertainty principle, Proc. Am. Math. Soc. 123 (1995), 1897–1905.Google Scholar
Bellazzini, J., Frank, R. L. and Visciglia, N., Maximizers for Gagliardo–Nirenberg inequalities and related non-local problems, Math. Ann. 360 (2014), 653–673.CrossRefGoogle Scholar
Bellazzini, J., Ghimenti, M., Mercuri, C., Moroz, V. and Van Schaftingen, J., Sharp Gagliardo–Nirenberg inequalities in fractional Coulomb–Sobolev spaces, Trans. Am. Math. Soc. 370 (2018), 8285–8310.CrossRefGoogle Scholar
Brezis, H., Van Schaftingen, J. and Yung, P. L., A surprising formula for Sobolev norms, Proc. Natl Acad. Sci. 118 (2021), e2025254118.Google ScholarPubMed
Brué, E. and Nguyen, Q. H., On the Sobolev space of functions with derivative of logarithmic order, Adv. Nonlinear Anal. 9 (2020), 836–849.CrossRefGoogle Scholar
Carlen, E. and Loss, M., Competing symmetries, the logarithmic HLS inequality and Onofri’s inequality on Sn, Geom. Funct. Anal. 2 (1992), 90–104.CrossRefGoogle Scholar
Crismale, V., De Luca, L., Kubin, A., Ninno, A. and Ponsiglione, M., The variational approach to s-fractional heat flows and the limit cases $s\rightarrow 0^+$ and $s\rightarrow 1^-$, J. Funct. Anal. 284 (2023), 109851.Google Scholar
De Carli, L., On the Lp–Lq norm of the Hankel transform and related operators, J. Math. Anal. Appl. 348 (2008), 366–382 pp.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., Hitchhiker’s guide to the fractional Sobolev spaces, Bull. Sci. Math. 136 (2012), 521–573.Google Scholar
Gorbachev, D., Liflyand, E. and Tikhonov, S., Weighted norm inequalities for integral transforms, Indiana Univ. Math. J. 67 (2018), 1949–2003.CrossRefGoogle Scholar
Lieb, E. H. and Loss, M., Analysis. CRM Proceedings & Lecture Notes, Volume 14, (American Mathematical Society, 2001).Google Scholar
Rubin, B. S., One-dimensional representation, inversion and certain properties of Riesz potentials of radial functions, Mat. Zametki 34 (1983), 521–533.Google Scholar
Stein, E. M., Interpolation of linear operators, Trans. Am. Math. Soc. 83 (1956), 482–492.CrossRefGoogle Scholar
Stein, E. M. and Weiss, G., Introduction to Fourier Analysis on Euclidean Spaces (PMS-32) (Princeton University Press, 1971).Google Scholar
Beckner, W., Pitt’s inequality with sharp convolution estimates, Proc. Amer. Math. Soc. 136 (2008), 1871–1885.CrossRefGoogle Scholar