Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T00:50:42.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattices whose ideal lattice is Stone

Published online by Cambridge University Press:  20 January 2009

R. Beazer
R. Beazer
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An elementary fact about ideal lattices of bounded distributive lattices is that they belong to the equational class ℬω of all distributive p-algebras (distributive lattices with pseudocomplementation). The lattice of equational subclasses of ℬω is known to be a chain

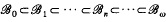
of type (ω+l, where ℬ0 is the class of Boolean algebras and ℬ1 is the class of Stone algebras. G. Grätzer in his book [7] asks after a characterisation of those bounded distributive lattices whose ideal lattice belongs to ℬ (n≧1). The answer to the problem for the case n = 0 is well known: the ideal lattice of a bounded lattice L is Boolean if and only if L is a finite Boolean algebra. D. Thomas [10] recently solved the problem for the case n = 1 utilising the order-topological duality theory for bounded distributive lattices and in [5] W. Bowen obtained another proof of Thomas's result via a construction of the dual space of the ideal lattice of a bounded distributive lattice from its dual space. In this paper we give a short, purely algebraic proof of Thomas's result and deduce from it necessary and sufficient conditions for the ideal lattice of a bounded distributive lattice to be a relative Stone algebra.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 1 , February 1983 , pp. 107 - 112
Copyright
Copyright © Edinburgh Mathematical Society 1983

References

REFERENCES

1.Balbes, R. and Dwinger, Ph., Distributive Lattices (Univ. Missouri Press, Columbia, Missouri, 1974).Google Scholar
2.Beazer, R., The determination congruence on double p-algebras, Algebra Universalis 6 (1976), 121–129.CrossRefGoogle Scholar
3.Beazer, R., Regular double p-algebras with Stone congruence lattices, Algebra Universalis 9 (1979), 238–243.CrossRefGoogle Scholar
4.Blyth, T. S., Ideals and filters of pseudo-complemented semilattices, Proc. Edinburgh Math. Soc. 23 (1980), 301–316.CrossRefGoogle Scholar
5.Bowen, W., Lattice Theory and Topology (Ph.D. thesis, Oxford, 1981).Google Scholar
6.Cornish, W., Congruences on distributive pseudocomplemented lattices, Bull. Austral. Math.Soc. 8 (1973), 161–179.CrossRefGoogle Scholar
7.Grätzer, G., General Lattice Theory (Birkhäuser Verlag, Basel, 1978).CrossRefGoogle Scholar
8.Katriñák, T., The structure of distributive double p-algebras. Regularity and congruences, Algebra Universalis 3 (1973), 238–246.CrossRefGoogle Scholar
9.Köhler, P., A subdirectly irreducible double Heyting algebra which is not simple, Algebra Universalis 10 (1980), 189–194.CrossRefGoogle Scholar
10.Thomas, D., Problems in Functional Analysis (Ph.D. thesis, Oxford, 1976).Google Scholar