Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-24T21:02:06.904Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice packing of nearly-euclidean balls in spaces of even dimension

Published online by Cambridge University Press:  20 January 2009

J. A. Rush
J. A. Rush
Affiliation:
Department of Mathematics, Box 354350 University of Washington Seattle, WA 98195 USA E-mail address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider nearly-Euclidean balls of the shape

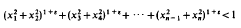
where ε is a small positive number, and n is even. If ε is small enough, then the maximum lattice-packing density of this body is essentially greater than the Minkowski-Hlawka bound for large n.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 39 , Issue 1 , February 1996 , pp. 163 - 169
Copyright
Copyright © Edinburgh Mathematical Society 1996

References

REFERENCES

1. Abramowitz, M. and Stegun, I. A., eds., Handbook of Mathematical Functions (National Bureau of Standards, 1965; and Dover 1966).Google Scholar
2. Cassels, J. W. S., An Introduction to the Geometry of Numbers (Springer-Verlag, N.Y., 1959).CrossRefGoogle Scholar
3. Conway, J. H. and Sloane, N. J. A., Sphere Packings, Lattices and Groups (Springer-Verlag, N.Y., 1987).Google Scholar
4. Elkies, N. D., Odlyzko, A. M. and Rush, J. A., On the packing densities of superballs and other bodies, Invent. Math. 105 (1991), 613–639.Google Scholar
5. Erdélyi, A., Asymptotic Expansions (Dover, 1956).Google Scholar
6. Gruber, P. M. and Lekkerkerker, C. G., Geometry of Numbers (Elsevier, North-Holland, Amsterdam, 1987).Google Scholar
7. Hlawka, E., Zur Geometric der Zahlen, Math. Z. 49 (1943), 285–312.CrossRefGoogle Scholar
8. Minkowski, H., Geometric der Zahlen (I. Leipzig, B. G. Teubner, 1896).Google Scholar
9. Minkowski, H., Gesammelte Abhandlungen (Chelsea, N.Y. (reprint), 1969).Google Scholar
10. Rogers, C. A., Packing and Covering Cambridge University Press, 1964).Google Scholar
11. Rush, J. A. and Sloane, N. J. A., An improvement to the Minkowski-Hlawka bound for packing superballs, Mathematika 34 (1987), 8–18.CrossRefGoogle Scholar
12. Rush, J. A., A lower bound on packing density, Invent. Math. 98 (1989), 499–509.Google Scholar
13. Rush, J. A., A bound, and a conjecture, on the maximum lattice-packing density of a superball, Mathematika 40 (1993), 137–143.Google Scholar