Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-17T01:28:10.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Lamplighter groups, median spaces and Hilbertian geometry

Part of: Special aspects of infinite or finite groups

Published online by Cambridge University Press:  09 June 2022

Anthony Genevois
Anthony Genevois*
Affiliation:
Institut Montpellierain Alexander Grothendieck, 499-554 Rue du Truel, 34090 Montpellier, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

From any two median spaces $X$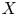 and $Y$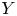, we construct a new median space $X \circledast Y$, referred to as the diadem product of $X$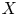 and $Y$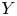, and we show that this construction is compatible with wreath products in the following sense: given two finitely generated groups $G,\,H$ 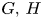and two (equivariant) coarse embeddings into median spaces $X,\,Y$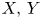, there exist a(n equivariant) coarse embedding $G\wr H \to X \circledast Y$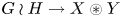. The construction offers a unified point of view on various questions related to the Hilbertian geometry of wreath products of groups.

Keywords

Wreath productsmedian spacesCAT(0) cube complexescompressionHaagerup propertyKazhdan property (T)

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 500 - 529
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arzhantseva, G., Guba, V. and Sapir, M., Metrics on diagram groups and uniform embeddings in a Hilbert space, Comment. Math. Helv. 81(4) (2006), 911–929.CrossRefGoogle Scholar
Austin, T., Naor, A. and Peres, Y., The wreath product of $\Bbb Z$ with $\Bbb Z$ has Hilbert compression exponent $\frac {2}3$, Proc. Amer. Math. Soc. 137(1) (2009), 85–90.CrossRefGoogle Scholar
Baudier, F., Motakis, P., Schlumprecht, T. and Zsák, A., On the bi-Lipschitz geometry of lamplighter graphs. preprint arXiv:1902.07098, to appear in Discrete Comput. Geom., 2019.Google Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan's property (T), New Mathematical Monographs, Volume 11 (Cambridge University Press, Cambridge, 2008).CrossRefGoogle Scholar
Bourgain, J., The metrical interpretation of superreflexivity in Banach spaces, Israel J. Math. 56(2) (1986), 222–230.CrossRefGoogle Scholar
Brieussel, J. and Zheng, T., Speed of random walks, isoperimetry and compression of finitely generated groups, Ann. Math. (2) 193(1) (2021), 1–105.CrossRefGoogle Scholar
Cave, C. and Dreesen, D., Embeddability of generalised wreath products, Bull. Aust. Math. Soc. 91(2) (2015), 250–263.CrossRefGoogle Scholar
Chatterji, I., Druţu, C. and Haglund, F., Kazhdan and Haagerup properties from the median viewpoint, Adv. Math. 225 (2010), 882–921.CrossRefGoogle Scholar
Chepoi, V., Graphs of some ${\rm CAT}(0)$ complexes, Adv. Appl. Math. 24(2) (2000), 125–179.CrossRefGoogle Scholar
Cherix, P.-A., Martin, F. and Valette, A., Spaces with measured walls, the Haagerup property and property (T), Ergodic Theory Dynam. Syst. 24(6) (2004), 1895–1908.CrossRefGoogle Scholar
Cornulier, Y., Stalder, Y. and Valette, A., Proper actions of wreath products and generalizations, Trans. Amer. Math. Soc. 364 (2012), 3159–3184.CrossRefGoogle Scholar
Genevois, A., Cubical-like geometry of quasi-median graphs and applications to geometric group theory. PhD Thesis, preprint arXiv:1712.01618, 2017.Google Scholar
Li, S., Compression bounds for wreath products, Proc. Amer. Math. Soc. 138(8) (2010), 2701–2714.CrossRefGoogle Scholar
Leemann, P.-H. and Schneeberger, G., Property FW and wreath products of groups: a simple approach using Schreier graphs. preprint arXiv:2101.03817, 2021Google Scholar
Nowak, P., On coarse embeddability into $l_p$-spaces and a conjecture of Dranishnikov, Fund. Math. 189(2) (2006), 111–116.CrossRefGoogle Scholar
Naor, A. and Peres, Y., Embeddings of discrete groups and the speed of random walks. Int. Math. Res. Not. IMRN, pages Art. ID rnn 076, 34, 2008CrossRefGoogle Scholar
Naor, A. and Peres, Y., $L_p$ compression, traveling salesmen, and stable walks, Duke Math. J. 157(1) (2011), 53–108.CrossRefGoogle Scholar
Parry, W., Growth series of some wreath products, Trans. Amer. Math. Soc. 331(2) (1992), 751–759.CrossRefGoogle Scholar
Roller, M., Pocsets, median algebras and group actions; an extended study of Dunwoody's construction and Sageev's theorem. dissertation, 1998Google Scholar
Stalder, Y. and Valette, A., Wreath products with the integers, proper actions and Hilbert space compression, Geom. Dedicata 124 (2007), 199–211.CrossRefGoogle Scholar
Tessera, R., Asymptotic isoperimetry on groups and uniform embeddings into Banach spaces, Comment. Math. Helv. 86(3) (2011), 499–535.CrossRefGoogle Scholar
Van de Vel, M., Theory of convex structures (North-Holland, Amsterdam, 1993).Google Scholar
Yu, G., The coarse Baum-Connes conjecture for spaces which admit a uniform embedding into Hilbert space, Invent. Math. 139(1) (2000), 201–240.CrossRefGoogle Scholar