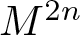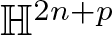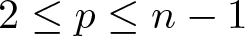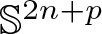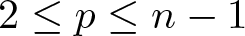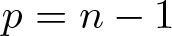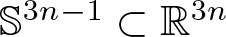The study of isometric immersions of Kaehler manifolds ![]() $(M^{2n},J)$,
$(M^{2n},J)$, ![]() $n\geq 2$, into spheres
$n\geq 2$, into spheres ![]() $\mathbb{S}^{2n+p}$ and hyperbolic spaces
$\mathbb{S}^{2n+p}$ and hyperbolic spaces ![]() $\mathbb{H}^{2n+p}$ with low codimension p was initiated by Ryan [Reference Ryan8]. He showed that for hypersurfaces there is only
$\mathbb{H}^{2n+p}$ with low codimension p was initiated by Ryan [Reference Ryan8]. He showed that for hypersurfaces there is only ![]() $M^4=\mathbb{S}^2\times\mathbb{S}^2\subset\mathbb{S}^5\subset\mathbb{R}^6$ in the sphere and that in the hyperbolic space there is
$M^4=\mathbb{S}^2\times\mathbb{S}^2\subset\mathbb{S}^5\subset\mathbb{R}^6$ in the sphere and that in the hyperbolic space there is ![]() $M^4=\mathbb{H}^2\times\mathbb{S}^2\subset\mathbb{H}^5\subset\mathbb{L}^6$ besides the even dimensional horospheres. Later on, Dajczer-Rodríguez [Reference Dajczer and Rodríguez3] proved that, regardless of the codimension, such isometric immersions do not occur if we require minimality.
$M^4=\mathbb{H}^2\times\mathbb{S}^2\subset\mathbb{H}^5\subset\mathbb{L}^6$ besides the even dimensional horospheres. Later on, Dajczer-Rodríguez [Reference Dajczer and Rodríguez3] proved that, regardless of the codimension, such isometric immersions do not occur if we require minimality.
The possibilities for Kaehler submanifolds with low codimension in spheres are rather restricted. In fact, it was shown by Florit–Hui–Zheng [Reference Florit, Hui and Zheng7] that if we have an isometric immersion into the unit sphere  $f\colon M^{2n}\to\mathbb{S}^{2n+p}_1$ with
$f\colon M^{2n}\to\mathbb{S}^{2n+p}_1$ with ![]() $p\leq n-1$, then
$p\leq n-1$, then ![]() $p=n-1$ and
$p=n-1$ and ![]() $f(M)\subset{\mathbb{S}}^{3n-1}_1\subset\mathbb{R}^{3n} = {\mathbb{R}}^3\times\cdots\times\mathbb{R}^3$ is an open subset of a Riemannian product of umbilical spheres
$f(M)\subset{\mathbb{S}}^{3n-1}_1\subset\mathbb{R}^{3n} = {\mathbb{R}}^3\times\cdots\times\mathbb{R}^3$ is an open subset of a Riemannian product of umbilical spheres  $\{\mathbb{S}^2_{c_j}\}_{1\leq j\leq n}$ in
$\{\mathbb{S}^2_{c_j}\}_{1\leq j\leq n}$ in ![]() $\mathbb{R}^3$ such that
$\mathbb{R}^3$ such that ![]() $1/c_1+\cdots+1/c_n=1$.
$1/c_1+\cdots+1/c_n=1$.
In [Reference Florit, Hui and Zheng7], it was observed that for submanifolds in hyperbolic space, a similar result as theirs is not possible due to the presence of the horospheres. In fact, there are the compositions ![]() $f=j\circ g$, where
$f=j\circ g$, where ![]() $j\colon{\mathbb{R}}^{2n+p-1}\to\mathbb{H}^{2n+p}$ is a horosphere and
$j\colon{\mathbb{R}}^{2n+p-1}\to\mathbb{H}^{2n+p}$ is a horosphere and ![]() $g\colon M^{2n}\to{\mathbb{R}}^{2n+p-1}$ an isometric immersion. In that respect, we observe that for any codimension, there is an abundance of non-holomorphic Kaehler submanifolds, a class intensively studied in the last 25 years with emphasis on the ones that are minimal. For an account of the basic facts on the subject of real Kaehler submanifolds, we refer to Chapter 15 in [Reference Dajczer and Tojeiro4] and the references listed in [Reference Dajczer and Vlachos5].
$g\colon M^{2n}\to{\mathbb{R}}^{2n+p-1}$ an isometric immersion. In that respect, we observe that for any codimension, there is an abundance of non-holomorphic Kaehler submanifolds, a class intensively studied in the last 25 years with emphasis on the ones that are minimal. For an account of the basic facts on the subject of real Kaehler submanifolds, we refer to Chapter 15 in [Reference Dajczer and Tojeiro4] and the references listed in [Reference Dajczer and Vlachos5].
The main goal of this paper is to locally characterize the submanifolds described next.
Example 1. Let the Kaehler manifold ![]() $M^{2n}$ be the Riemannian product of a hyperbolic plane and a set of two-dimensional round spheres given by
$M^{2n}$ be the Riemannian product of a hyperbolic plane and a set of two-dimensional round spheres given by
 \begin{equation*}
M^{2n}=\mathbb{H}^2_{c_1}\times\mathbb{S}^2_{c_2}\times\cdots\times\mathbb{S}^2_{c_n}
\quad \textrm{with}\ 1/c_1+\cdots +1/c_n=-1.
\end{equation*}
\begin{equation*}
M^{2n}=\mathbb{H}^2_{c_1}\times\mathbb{S}^2_{c_2}\times\cdots\times\mathbb{S}^2_{c_n}
\quad \textrm{with}\ 1/c_1+\cdots +1/c_n=-1.
\end{equation*} Then let ![]() $f\colon M^{2n}\to\mathbb{H}^{3n-1}_{-1}$ be the submanifold defined by
$f\colon M^{2n}\to\mathbb{H}^{3n-1}_{-1}$ be the submanifold defined by ![]() $g=i\circ f\colon M^{2n}\to\mathbb{L}^{3n}$, where
$g=i\circ f\colon M^{2n}\to\mathbb{L}^{3n}$, where ![]() $i\colon\mathbb{H}^{3n-1}\to\mathbb{L}^{3n}$ is the inclusion into the flat Lorentzian space
$i\colon\mathbb{H}^{3n-1}\to\mathbb{L}^{3n}$ is the inclusion into the flat Lorentzian space ![]() $\mathbb{L}^{3n}=\mathbb{L}^3\times\mathbb{R}^3\times\cdots\times\mathbb{R}^3$ and
$\mathbb{L}^{3n}=\mathbb{L}^3\times\mathbb{R}^3\times\cdots\times\mathbb{R}^3$ and ![]() $g=g_1\times g_2\times\cdots\times g_n$ is the extrinsic product of umbilical surfaces
$g=g_1\times g_2\times\cdots\times g_n$ is the extrinsic product of umbilical surfaces  $g_1\colon \mathbb{H}^2_{c_1}\to\mathbb{L}^3$ and
$g_1\colon \mathbb{H}^2_{c_1}\to\mathbb{L}^3$ and  $g_j\colon\mathbb{S}^2_{c_j}\to\mathbb{R}^3$,
$g_j\colon\mathbb{S}^2_{c_j}\to\mathbb{R}^3$, ![]() $2\leq j\leq n$.
$2\leq j\leq n$.
To make our goal feasible, it is necessary to remove the possibility for the submanifold to lay inside a horosphere. Such a task is fulfilled here inspired by the following sharp estimate given as Corollary 15.6 in [Reference Dajczer and Tojeiro4].
Let ![]() $f\colon M^{2n}\to\mathbb{R}^{2n+p}$,
$f\colon M^{2n}\to\mathbb{R}^{2n+p}$, ![]() $1\leq p\leq n-1$, be an isometric immersion of a Kaehler manifold. At any
$1\leq p\leq n-1$, be an isometric immersion of a Kaehler manifold. At any ![]() $x\in M^{2n}$, there is a complex vector subspace
$x\in M^{2n}$, there is a complex vector subspace ![]() $L^{2\ell}\subset T_xM$ with
$L^{2\ell}\subset T_xM$ with ![]() $\ell\geq n-p$ such that the sectional curvature of
$\ell\geq n-p$ such that the sectional curvature of ![]() $M^{2n}$ satisfies
$M^{2n}$ satisfies ![]() $K(Z,JZ)\leq 0$ for any
$K(Z,JZ)\leq 0$ for any ![]() $Z\in L^{2\ell}$.
$Z\in L^{2\ell}$.
The following is the main result of this paper.
Theorem 2. Let  $f\colon M^{2n}\to\mathbb{H}^{2n+p}_{-1}$,
$f\colon M^{2n}\to\mathbb{H}^{2n+p}_{-1}$, ![]() $p\leq n-1$, be an isometric immersion of a Kaehler manifold. Assume that at some point
$p\leq n-1$, be an isometric immersion of a Kaehler manifold. Assume that at some point ![]() $x_0\in M^{2n}$, there is a complex vector subspace
$x_0\in M^{2n}$, there is a complex vector subspace  $V^{2m}\subset T_{x_0}M$ with
$V^{2m}\subset T_{x_0}M$ with ![]() $m\geq p$ such that the sectional curvature of
$m\geq p$ such that the sectional curvature of ![]() $M^{2n}$ satisfies
$M^{2n}$ satisfies ![]() $K(S,JS) \gt 0$ for any
$K(S,JS) \gt 0$ for any ![]() $0\neq S\in V^{2m}$. Then
$0\neq S\in V^{2m}$. Then ![]() $p=n-1$ and f(M) is an open subset of the submanifold given by Example 1.
$p=n-1$ and f(M) is an open subset of the submanifold given by Example 1.
The remaining of this paper is devoted to generalize several results by Dajczer and Vlachos [Reference Dajczer and Vlachos5]. The following result improves their Theorem 7 that deals with the size of the dimension of the complex subspaces where the holomorphic sectional curvature is non-positive. In addition, we establish an estimate for the Ricci curvature. Moreover, in both cases, the estimates now obtained are sharp.
Theorem 3. Let ![]() $f\colon M^{2n}\to\mathbb{H}^{2n+p}$,
$f\colon M^{2n}\to\mathbb{H}^{2n+p}$, ![]() $1\leq p\leq n-2$, be an isometric immersion of a Kaehler manifold. At any point
$1\leq p\leq n-2$, be an isometric immersion of a Kaehler manifold. At any point ![]() $x\in M^{2n}$, there is a complex vector subspace
$x\in M^{2n}$, there is a complex vector subspace ![]() $V^{2\ell}\subset T_xM$ with
$V^{2\ell}\subset T_xM$ with ![]() $\ell\geq n-p+1$ such that for any
$\ell\geq n-p+1$ such that for any ![]() $S\in V^{2\ell}$, the sectional curvature of
$S\in V^{2\ell}$, the sectional curvature of ![]() $M^{2n}$ satisfies
$M^{2n}$ satisfies ![]() $K(S,JS)\leq 0$ and the Ricci curvature that
$K(S,JS)\leq 0$ and the Ricci curvature that ![]() $Ric(S)\leq 0$.
$Ric(S)\leq 0$.
For p = 1, the above estimates follow trivially from the aforementioned result due to Ryan. For codimension p = 2, they are a consequence of Theorem 1 in [Reference Dajczer and Vlachos5] and, as is the case for p = 1, with the stronger assertions ![]() $K(S,JS)=0=Ric(S)$. It is shown in [Reference Dajczer and Vlachos5] that locally
$K(S,JS)=0=Ric(S)$. It is shown in [Reference Dajczer and Vlachos5] that locally ![]() $f=j\circ g$ is a composition as given above. To reach that conclusion, one has to use the non-flat Kaehler hypersurfaces in Euclidean space, whose classification can be seen in [Reference Dajczer and Tojeiro4] as Theorem 15.14, which have only two non-zero simple principal curvatures. In particular, observe that when the hypersurface has a plane of positive sectional curvature, these examples show that Theorem 3 is sharp already for p = 2.
$f=j\circ g$ is a composition as given above. To reach that conclusion, one has to use the non-flat Kaehler hypersurfaces in Euclidean space, whose classification can be seen in [Reference Dajczer and Tojeiro4] as Theorem 15.14, which have only two non-zero simple principal curvatures. In particular, observe that when the hypersurface has a plane of positive sectional curvature, these examples show that Theorem 3 is sharp already for p = 2.
From the two results above, we obtain the following generalization of Theorem 3 in [Reference Dajczer and Vlachos5] given there for codimension ![]() $p\leq n-2$.
$p\leq n-2$.
Corollary 4. A Kaehler manifold ![]() $M^{2n}$,
$M^{2n}$, ![]() $n\geq 2$, that at some point possesses positive holomorphic sectional curvature cannot be isometrically immersed in
$n\geq 2$, that at some point possesses positive holomorphic sectional curvature cannot be isometrically immersed in ![]() $\mathbb{H}^{3n-1}$.
$\mathbb{H}^{3n-1}$.
The next result was obtained in [Reference Dajczer and Vlachos5] for ![]() $p\leq n-2$ under the weaker hypothesis that the Omori-Yau weak maximum principle for the Hessian holds on
$p\leq n-2$ under the weaker hypothesis that the Omori-Yau weak maximum principle for the Hessian holds on ![]() $M^{2n}$. Under the assumptions that the Riemannian manifold is complete with sectional curvature bounded from below, we have from Theorem 2.3 in [Reference Alías, Mastrolia and Rigoli1] that the Omori-Yau maximum principle for the Hessian holds.
$M^{2n}$. Under the assumptions that the Riemannian manifold is complete with sectional curvature bounded from below, we have from Theorem 2.3 in [Reference Alías, Mastrolia and Rigoli1] that the Omori-Yau maximum principle for the Hessian holds.
Theorem 5. Let ![]() $f\colon M^{2n}\to\mathbb{H}^{3n-1}$ be an isometric immersion of a complete Kaehler manifold with sectional curvature bounded from below. Then f(M) is unbounded.
$f\colon M^{2n}\to\mathbb{H}^{3n-1}$ be an isometric immersion of a complete Kaehler manifold with sectional curvature bounded from below. Then f(M) is unbounded.
Finally, we consider the case of submanifolds with codimension two.
Theorem 6. Let ![]() $f\colon M^{2n}\to\mathbb{H}^{2n+2}$,
$f\colon M^{2n}\to\mathbb{H}^{2n+2}$, ![]() $n\geq 3$, be an isometric immersion of a Kaehler manifold which does not contain an open subset of flat points. Then either n = 3 and
$n\geq 3$, be an isometric immersion of a Kaehler manifold which does not contain an open subset of flat points. Then either n = 3 and ![]() $M^6\subset\mathbb{H}^2\times\mathbb{S}^2\times\mathbb{S}^2\subset\mathbb{H}^8\subset\mathbb{L}^9$ or there is a composition of isometric immersion
$M^6\subset\mathbb{H}^2\times\mathbb{S}^2\times\mathbb{S}^2\subset\mathbb{H}^8\subset\mathbb{L}^9$ or there is a composition of isometric immersion ![]() $f=j\circ g$, where
$f=j\circ g$, where ![]() $g\colon M^{2n}\to\mathbb{R}^{2n+1}$ is a real Kaehler hypersurface and
$g\colon M^{2n}\to\mathbb{R}^{2n+1}$ is a real Kaehler hypersurface and ![]() $j\colon\mathbb{R}^{2n+1}\to\mathbb{H}^{2n+2}$ is a horosphere.
$j\colon\mathbb{R}^{2n+1}\to\mathbb{H}^{2n+2}$ is a horosphere.
In addition, the result extends Theorem 1 in [Reference Dajczer and Vlachos5] by including the case n = 3. Moreover, it generalizes this result as well as Theorem 6 in [Reference Dajczer and Vlachos5] since now it is global and, with respect to the latter, it does not require to assume flat normal bundle.
1. Several algebraic considerations
1.1. Some general facts
Let ![]() $W^{p,p}$ denote a real vector space of dimension 2p endowed with an indefinite inner product of signature (p, p). Thus, p is the maximal dimension of a vector subspace such that the induced inner product is either positive or negative definite. A vector subspace
$W^{p,p}$ denote a real vector space of dimension 2p endowed with an indefinite inner product of signature (p, p). Thus, p is the maximal dimension of a vector subspace such that the induced inner product is either positive or negative definite. A vector subspace ![]() $L\subset W^{p,p}$ is called degenerate if
$L\subset W^{p,p}$ is called degenerate if ![]() $L\cap L^\perp\neq 0$ and nondegenerate if otherwise. Moreover, a vector subspace L ≠ 0 is called isotropic if it satisfies
$L\cap L^\perp\neq 0$ and nondegenerate if otherwise. Moreover, a vector subspace L ≠ 0 is called isotropic if it satisfies ![]() $L=L\cap L^\perp$.
$L=L\cap L^\perp$.
The following result is Sublemma 2.3 in [Reference do Carmo and Dajczer6] and Corollary 4.3 in [Reference Dajczer and Tojeiro4].
Proposition 7. Given a vector subspace ![]() $L\subset W^{p,p}$, there is a direct sum decomposition
$L\subset W^{p,p}$, there is a direct sum decomposition ![]() $W^{p,p}=\mathcal{U}\oplus\hat{\mathcal{U}}\oplus\mathcal{V}$, where
$W^{p,p}=\mathcal{U}\oplus\hat{\mathcal{U}}\oplus\mathcal{V}$, where ![]() $\mathcal{U}=L\cap L^\perp$ such that the vector subspace
$\mathcal{U}=L\cap L^\perp$ such that the vector subspace ![]() $\hat{\mathcal{U}}$ is isotropic, the vector subspace
$\hat{\mathcal{U}}$ is isotropic, the vector subspace ![]() $\mathcal{V}=(\mathcal{U}\oplus\hat{\mathcal{U}})^\perp$ is non-degenerate and
$\mathcal{V}=(\mathcal{U}\oplus\hat{\mathcal{U}})^\perp$ is non-degenerate and ![]() $L\subset\mathcal{U}\oplus\mathcal{V}$.
$L\subset\mathcal{U}\oplus\mathcal{V}$.
Let V be a finite-dimensional real vector space and ![]() $\varphi\colon V\times V\to W^{p,p}$ a bilinear form. Then φ is called a flat bilinear form if
$\varphi\colon V\times V\to W^{p,p}$ a bilinear form. Then φ is called a flat bilinear form if
for all ![]() $X,Z,Y,T\in V$. We denote the vector subspace generated by φ by
$X,Z,Y,T\in V$. We denote the vector subspace generated by φ by
and say that φ is surjective if ![]() $\mathcal{S}(\varphi)=W^{p,p}$. The (right) kernel φ is defined by
$\mathcal{S}(\varphi)=W^{p,p}$. The (right) kernel φ is defined by
If ![]() $V_1,V_2\subset V$ are vector subspaces, we denote
$V_1,V_2\subset V$ are vector subspaces, we denote
A vector ![]() $X\in V$ is called a (left) regular element of φ if
$X\in V$ is called a (left) regular element of φ if ![]() $\dim\varphi_X(V)=r$, where
$\dim\varphi_X(V)=r$, where
and ![]() $\varphi_X\colon V\to W^{p,p}$ is the linear transformation defined by
$\varphi_X\colon V\to W^{p,p}$ is the linear transformation defined by
The set ![]() ${\rm RE}(\varphi)$ of regular elements of φ is easily seen to be an open dense subset of V; for instance, see Proposition 4.4 in [Reference Dajczer and Tojeiro4].
${\rm RE}(\varphi)$ of regular elements of φ is easily seen to be an open dense subset of V; for instance, see Proposition 4.4 in [Reference Dajczer and Tojeiro4].
Proposition 8. Let ![]() $\varphi\colon V\times V\to W^{p,p}$ be a flat bilinear form. If
$\varphi\colon V\times V\to W^{p,p}$ be a flat bilinear form. If ![]() $X\in RE(\varphi)$, then
$X\in RE(\varphi)$, then
 \begin{equation}
{\cal S}(\varphi|_{V\times \ker\varphi_X})\subset
\varphi_X(V)\cap(\varphi_X(V))^\perp.
\end{equation}
\begin{equation}
{\cal S}(\varphi|_{V\times \ker\varphi_X})\subset
\varphi_X(V)\cap(\varphi_X(V))^\perp.
\end{equation}Proof. See Sublemma 2.4 in [Reference do Carmo and Dajczer6] or Proposition 4.6 in [Reference Dajczer and Tojeiro4].
1.2. A general bilinear form
Let ![]() $V^{2n}$ and
$V^{2n}$ and ![]() $\mathbb{L}^p$,
$\mathbb{L}^p$, ![]() $p\geq 2$, be real vector spaces such that there is
$p\geq 2$, be real vector spaces such that there is ![]() $J\in Aut(V)$, which satisfies
$J\in Aut(V)$, which satisfies ![]() $J^2=-I$, and
$J^2=-I$, and ![]() $\mathbb{L}^p$ is endowed with a Lorentzian inner product
$\mathbb{L}^p$ is endowed with a Lorentzian inner product ![]() $\langle\,,\,\rangle$. Then let
$\langle\,,\,\rangle$. Then let ![]() $W^{p,p}=\mathbb{L}^p\oplus\mathbb{L}^p$ be endowed with the inner product of signature (p, p) defined by
$W^{p,p}=\mathbb{L}^p\oplus\mathbb{L}^p$ be endowed with the inner product of signature (p, p) defined by
Let ![]() $\alpha\colon V^{2n}\times V^{2n}\to\mathbb{L}^p$ be a symmetric bilinear form, and then let the bilinear form
$\alpha\colon V^{2n}\times V^{2n}\to\mathbb{L}^p$ be a symmetric bilinear form, and then let the bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be defined by
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be defined by
Then β satisfies
for any ![]() $X,Y\in V^{2n}$. Notice that
$X,Y\in V^{2n}$. Notice that ![]() $\beta(X,X)=(\zeta,0)$ for
$\beta(X,X)=(\zeta,0)$ for ![]() $X\in V^{2n}$ and
$X\in V^{2n}$ and ![]() $\zeta\in\mathbb{L}^p$. Moreover, if
$\zeta\in\mathbb{L}^p$. Moreover, if ![]() $\beta(X,Y)=(\xi,\eta)$, then we have
$\beta(X,Y)=(\xi,\eta)$, then we have
In particular, it follows that ![]() $\mathcal{N}(\beta)$ is a J-invariant vector subspace of
$\mathcal{N}(\beta)$ is a J-invariant vector subspace of ![]() $V^{2n}$.
$V^{2n}$.
In the sequel, ![]() $U_0^s\subset\mathbb{L}^p$ is the s-dimensional vector subspace
$U_0^s\subset\mathbb{L}^p$ is the s-dimensional vector subspace ![]() $U_0^s=\pi_1({\cal S}(\beta))$, where
$U_0^s=\pi_1({\cal S}(\beta))$, where ![]() $\pi_1\colon W^{p,p}\to\mathbb{L}^p$ denotes the projection onto the first component of
$\pi_1\colon W^{p,p}\to\mathbb{L}^p$ denotes the projection onto the first component of ![]() $W^{p,p}$. Hence,
$W^{p,p}$. Hence,
Proposition 9. The bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ satisfies
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ satisfies
Moreover, if the vector subspace ![]() ${\cal S}(\beta)$ is degenerate, then
${\cal S}(\beta)$ is degenerate, then ![]() $1\leq s\leq p-1$, and there is a non-zero light-like vector
$1\leq s\leq p-1$, and there is a non-zero light-like vector ![]() $v\in U_0^s$ such that
$v\in U_0^s$ such that
Proof. If  $\sum_{j=1}^k\beta(X_j,Y_j)=(\xi,\eta)$, we obtain from Equation (5) that
$\sum_{j=1}^k\beta(X_j,Y_j)=(\xi,\eta)$, we obtain from Equation (5) that
 \begin{equation*}
\sum_{j=1}^k\beta(Y_j,X_j)=(\xi,-\eta),\quad
\sum_{j=1}^k\beta(X_j,JY_j)=(\eta,-\xi)\quad\textrm{and}\quad
\sum_{j=1}^k\beta(JY_j,X_j)=(\eta,\xi).
\end{equation*}
\begin{equation*}
\sum_{j=1}^k\beta(Y_j,X_j)=(\xi,-\eta),\quad
\sum_{j=1}^k\beta(X_j,JY_j)=(\eta,-\xi)\quad\textrm{and}\quad
\sum_{j=1}^k\beta(JY_j,X_j)=(\eta,\xi).
\end{equation*} Hence, ![]() $(\xi,0),(0,\xi),(\eta,0)\in{\cal S}(\beta)$ and thus
$(\xi,0),(0,\xi),(\eta,0)\in{\cal S}(\beta)$ and thus ![]() $\mathcal{S}(\beta)\subset U_0^s\oplus U_0^s$. If
$\mathcal{S}(\beta)\subset U_0^s\oplus U_0^s$. If ![]() $(\xi,\eta)\in U_0^s\oplus U_0^s$, there are
$(\xi,\eta)\in U_0^s\oplus U_0^s$, there are ![]() $\delta,\bar{\delta}\in \mathbb{L}^p$ such that
$\delta,\bar{\delta}\in \mathbb{L}^p$ such that ![]() $(\xi,\delta),(\eta,\bar{\delta})\in{\cal S}(\beta)$ and as just seen
$(\xi,\delta),(\eta,\bar{\delta})\in{\cal S}(\beta)$ and as just seen ![]() $(\xi,\eta)\in{\cal S}(\beta)$.
$(\xi,\eta)\in{\cal S}(\beta)$.
Since ![]() ${\cal S}(\beta)\neq 0$ and Equation (6) is satisfied, then if
${\cal S}(\beta)\neq 0$ and Equation (6) is satisfied, then if ![]() ${\cal S}(\beta)$ is a degenerate subspace, we have that
${\cal S}(\beta)$ is a degenerate subspace, we have that ![]() $1\leq s\leq p-1$. If
$1\leq s\leq p-1$. If ![]() $\mathcal{U}={\cal S}(\beta)\cap({\cal S}(\beta))^\perp$, we claim that
$\mathcal{U}={\cal S}(\beta)\cap({\cal S}(\beta))^\perp$, we claim that ![]() $\mathcal{U}=U_1\oplus U_1$, where
$\mathcal{U}=U_1\oplus U_1$, where ![]() $U_1=\pi_1(\mathcal{U})$. We have from Equation (5) that
$U_1=\pi_1(\mathcal{U})$. We have from Equation (5) that
and
Hence, if ![]() $(\xi,\eta)\in\mathcal{U}$, then also
$(\xi,\eta)\in\mathcal{U}$, then also ![]() $(\eta,-\xi)$,
$(\eta,-\xi)$, ![]() $(\xi,-\eta)$,
$(\xi,-\eta)$, ![]() $(\eta,\xi)\in\mathcal{U}$. Thus,
$(\eta,\xi)\in\mathcal{U}$. Thus, ![]() $(\xi,0),(0,\xi),(\eta,0)\in\mathcal{U}$ and hence
$(\xi,0),(0,\xi),(\eta,0)\in\mathcal{U}$ and hence ![]() $\mathcal{U}\subset U_1\oplus U_1$. If
$\mathcal{U}\subset U_1\oplus U_1$. If ![]() $(\xi,\eta)\in U_1\oplus U_1$, there are
$(\xi,\eta)\in U_1\oplus U_1$, there are ![]() $\delta,\bar{\delta}\in \mathbb{L}^p$ such that
$\delta,\bar{\delta}\in \mathbb{L}^p$ such that ![]() $(\xi,\delta),(\eta,\bar{\delta})\in\mathcal{U}$ and thus
$(\xi,\delta),(\eta,\bar{\delta})\in\mathcal{U}$ and thus ![]() $(\xi,\eta)\in\mathcal{U}$, proving the claim. It follows from Equation (2) and the claim that the vector subspace
$(\xi,\eta)\in\mathcal{U}$, proving the claim. It follows from Equation (2) and the claim that the vector subspace ![]() $U_1\subset\mathbb{L}^p$ is isotropic and thus Equation (7) holds.
$U_1\subset\mathbb{L}^p$ is isotropic and thus Equation (7) holds.
Given ![]() $X\in V^{2n}$, we denote
$X\in V^{2n}$, we denote ![]() $N(X)=\ker B_X$, where
$N(X)=\ker B_X$, where ![]() $B_X=\beta_X$. It follows from Equation (5) that the vector subspace N(X) is J-invariant.
$B_X=\beta_X$. It follows from Equation (5) that the vector subspace N(X) is J-invariant.
Lemma 10. Let the bilinear form β be flat and ![]() $X\in RE(\beta)$ satisfy
$X\in RE(\beta)$ satisfy ![]() $\beta|_{V\times N(X)}\neq 0$. Then there is a non-zero light-like vector
$\beta|_{V\times N(X)}\neq 0$. Then there is a non-zero light-like vector ![]() $v\in\mathbb{L}^p$ such that
$v\in\mathbb{L}^p$ such that
 \begin{equation}
{span}\{v\}\oplus{span}\{v\}\subset{\cal S}(\beta|_{V\times N(X)})\subset
B_X(V)\cap (B_X(V))^\perp.
\end{equation}
\begin{equation}
{span}\{v\}\oplus{span}\{v\}\subset{\cal S}(\beta|_{V\times N(X)})\subset
B_X(V)\cap (B_X(V))^\perp.
\end{equation} Moreover, if ![]() $(v^{\prime},w^{\prime})\in B_X(V)$, where
$(v^{\prime},w^{\prime})\in B_X(V)$, where ![]() $v^{\prime},w^{\prime}$ are light-like vectors, then
$v^{\prime},w^{\prime}$ are light-like vectors, then ![]() $v^{\prime},w^{\prime}\in\textrm{span}\{v\}$.
$v^{\prime},w^{\prime}\in\textrm{span}\{v\}$.
Proof. First notice that the second inclusion in Equation (8) is just Equation (1). If ![]() $\beta|_{N(X)\times N(X)}\neq 0$, then the vector subspace
$\beta|_{N(X)\times N(X)}\neq 0$, then the vector subspace ![]() ${\cal S}(\beta|_{N(X)\times N(X)})$ is isotropic. Then by Equation (7), there is
${\cal S}(\beta|_{N(X)\times N(X)})$ is isotropic. Then by Equation (7), there is ![]() $v\in\mathbb{L}^p$ such that
$v\in\mathbb{L}^p$ such that ![]() $\textrm{span}\{v\}\oplus\textrm{span}\{v\}={\cal S}(\beta|_{N(X)\times N(X)})$. Suppose that
$\textrm{span}\{v\}\oplus\textrm{span}\{v\}={\cal S}(\beta|_{N(X)\times N(X)})$. Suppose that ![]() $\beta|_{N(X)\times N(X)}=0$. By assumption, there are
$\beta|_{N(X)\times N(X)}=0$. By assumption, there are ![]() $Y\in V^{2n}$ and
$Y\in V^{2n}$ and ![]() $Z\in N(X)$ such that
$Z\in N(X)$ such that ![]() $\beta(Y,Z)=(v,w)\neq 0$. Since the vector subspace
$\beta(Y,Z)=(v,w)\neq 0$. Since the vector subspace ![]() ${\cal S}(\beta|_{V\times N(X)})$ is isotropic, we have
${\cal S}(\beta|_{V\times N(X)})$ is isotropic, we have
whereas from Equation (5) and the flatness of β, we obtain
Thus, the vectors ![]() $v,w\in\mathbb{L}^p$ are both light-like.
$v,w\in\mathbb{L}^p$ are both light-like.
It suffices to argue for v ≠ 0 since ![]() $\beta(Y,JZ)=(w,-v)$. Since N(X) is J-invariant and
$\beta(Y,JZ)=(w,-v)$. Since N(X) is J-invariant and ![]() ${\cal S}(\beta|_{V\times N(X)})$ is isotropic, we obtain using Equation (5) that
${\cal S}(\beta|_{V\times N(X)})$ is isotropic, we obtain using Equation (5) that
and hence w = av. Then from
we obtain the first inclusion in Equation (8).
Let ![]() $B_XZ=(v^{\prime},w^{\prime})$ be as in the statement. By Equation (8), we have
$B_XZ=(v^{\prime},w^{\prime})$ be as in the statement. By Equation (8), we have
and thus ![]() $v^{\prime}\in\textrm{span}\{v\}$. Since
$v^{\prime}\in\textrm{span}\{v\}$. Since ![]() $B_XJZ=(w^{\prime},-v^{\prime}),$ then also
$B_XJZ=(w^{\prime},-v^{\prime}),$ then also ![]() $w^{\prime}\in\textrm{span}\{v\}$.
$w^{\prime}\in\textrm{span}\{v\}$.
Proposition 11. Let the bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$,
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$, ![]() $p\leq n$, be surjective and flat. Then we have
$p\leq n$, be surjective and flat. Then we have
Moreover, if ![]() $\mathcal{N}(\beta)=0$ and
$\mathcal{N}(\beta)=0$ and ![]() $X\in RE(\beta)$, then
$X\in RE(\beta)$, then ![]() $B_X\colon V^{2n}\to W^{p,p}$ is an isomorphism.
$B_X\colon V^{2n}\to W^{p,p}$ is an isomorphism.
Proof. If ![]() $X\in RE(\beta)$, we have
$X\in RE(\beta)$, we have ![]() $\dim N(X)\geq 2n-2p$. Since
$\dim N(X)\geq 2n-2p$. Since ![]() $\mathcal{N}(\beta)\subset N(X)$, if we have that
$\mathcal{N}(\beta)\subset N(X)$, if we have that ![]() $N(X)=0$ for some
$N(X)=0$ for some ![]() $X\in RE(\beta)$, then the result holds trivially. Thus, it remains to argue when
$X\in RE(\beta)$, then the result holds trivially. Thus, it remains to argue when ![]() $N(X)\neq 0$ for any
$N(X)\neq 0$ for any ![]() $X\in RE(\beta)$. In this case, we also show that
$X\in RE(\beta)$. In this case, we also show that ![]() $\mathcal{N}(\beta)\neq 0$, and this gives the second statement.
$\mathcal{N}(\beta)\neq 0$, and this gives the second statement.
If ![]() $\beta|_{V\times N(X)}=0$ for some
$\beta|_{V\times N(X)}=0$ for some ![]() $X\in RE(\beta)$, then
$X\in RE(\beta)$, then ![]() $N(X)=\mathcal{N}(\beta)$. Then
$N(X)=\mathcal{N}(\beta)$. Then ![]() $\mathcal{N}(\beta)\neq 0$ and
$\mathcal{N}(\beta)\neq 0$ and ![]() $\dim\mathcal{N}(\beta)=\dim N(X)\geq 2n-2p$. Hence, we assume that
$\dim\mathcal{N}(\beta)=\dim N(X)\geq 2n-2p$. Hence, we assume that ![]() $\beta|_{V\times N(X)}\neq 0$ for any
$\beta|_{V\times N(X)}\neq 0$ for any ![]() $X\in RE(\beta)$. Fix a vector
$X\in RE(\beta)$. Fix a vector ![]() $X\in {\rm RE}(\beta)$. By Lemma 10, there is a non-zero light-like vector
$X\in {\rm RE}(\beta)$. By Lemma 10, there is a non-zero light-like vector ![]() $v\in\mathbb{L}^p$, such that
$v\in\mathbb{L}^p$, such that
On the one hand, since ![]() ${\cal S}(\beta)=W^{p,p}$ and the subset
${\cal S}(\beta)=W^{p,p}$ and the subset ![]() ${\rm RE}(\beta)$ is dense, there are
${\rm RE}(\beta)$ is dense, there are ![]() $Y\in RE(\beta)$ and
$Y\in RE(\beta)$ and ![]() $
Z\in V^{2n}$ such that
$
Z\in V^{2n}$ such that ![]() ${\langle\!\langle}\beta(Y,Z),(v,0){\rangle\!\rangle}\neq 0$. On the other hand, since
${\langle\!\langle}\beta(Y,Z),(v,0){\rangle\!\rangle}\neq 0$. On the other hand, since ![]() $Y\in RE(\beta)$, then Lemma 10 yields a non-zero light-like vector
$Y\in RE(\beta)$, then Lemma 10 yields a non-zero light-like vector ![]() $w\in\mathbb{L}^p$ such that
$w\in\mathbb{L}^p$ such that  $\textrm{span}\{w\}\oplus\textrm{span}\{w\}\subset{\cal S}(\beta|_{V\times N(Y)})
\subset B_Y(V)\cap(B_Y(V))^\perp$, and hence,
$\textrm{span}\{w\}\oplus\textrm{span}\{w\}\subset{\cal S}(\beta|_{V\times N(Y)})
\subset B_Y(V)\cap(B_Y(V))^\perp$, and hence, ![]() ${\langle\!\langle}\beta(Y,Z),(w,0){\rangle\!\rangle}=0$. Thus, the vectors v and w are linearly independent.
${\langle\!\langle}\beta(Y,Z),(w,0){\rangle\!\rangle}=0$. Thus, the vectors v and w are linearly independent.
From Equation (1), we obtain that ![]() $B_Y(N(X))\subset\mathcal{U}^\tau(X)$. If
$B_Y(N(X))\subset\mathcal{U}^\tau(X)$. If ![]() $(av,bv)\in B_Y(N(X))$, then the second part of Lemma 10 gives that
$(av,bv)\in B_Y(N(X))$, then the second part of Lemma 10 gives that ![]() $av,bv\in\textrm{span}\{w\}$, and hence,
$av,bv\in\textrm{span}\{w\}$, and hence, ![]() $a=b=0$. Thus,
$a=b=0$. Thus, ![]() $\textrm{span}\{v\}\oplus\textrm{span}\{v\}\cap B_Y(N(X))=0$. Consequently, for
$\textrm{span}\{v\}\oplus\textrm{span}\{v\}\cap B_Y(N(X))=0$. Consequently, for ![]() $B_Y|_{N(X)}\colon N(X)\to\mathcal{U}^\tau(X)$ and since
$B_Y|_{N(X)}\colon N(X)\to\mathcal{U}^\tau(X)$ and since ![]() $\textrm{span}\{v\}\oplus\textrm{span}\{v\}\subset \mathcal{U}^\tau(X)$, we have that
$\textrm{span}\{v\}\oplus\textrm{span}\{v\}\subset \mathcal{U}^\tau(X)$, we have that ![]() $N_1=\ker B_Y|_{N(X)}$ satisfies
$N_1=\ker B_Y|_{N(X)}$ satisfies
Proposition 7 applied to ![]() $B_X(V)\subset W^{p,p}$ yields a decomposition
$B_X(V)\subset W^{p,p}$ yields a decomposition
verifying that ![]() $B_X(V)\subset\mathcal{U}(X)\oplus\mathcal{V}$ among other properties. Thus,
$B_X(V)\subset\mathcal{U}(X)\oplus\mathcal{V}$ among other properties. Thus, ![]() $\dim B_X(V)\leq 2p-\tau$, and hence,
$\dim B_X(V)\leq 2p-\tau$, and hence, ![]() $\dim N(X)\geq 2n-2p+\tau$. It follows from Equation (10) that
$\dim N(X)\geq 2n-2p+\tau$. It follows from Equation (10) that ![]() $\dim N_1\geq 2n-2p+2\geq 2$.
$\dim N_1\geq 2n-2p+2\geq 2$.
We prove that ![]() $N_1=\mathcal{N}(\beta)$, which gives
$N_1=\mathcal{N}(\beta)$, which gives ![]() $\dim\mathcal{N}(\beta)\geq 2n-2p+2 \gt 0$, which is even a better estimate than Equation (9). Since
$\dim\mathcal{N}(\beta)\geq 2n-2p+2 \gt 0$, which is even a better estimate than Equation (9). Since ![]() $N_1=N(X)\cap N(Y)$ by Equation (1), then
$N_1=N(X)\cap N(Y)$ by Equation (1), then ![]() ${\cal S}(\beta|_{N_1\times N_1})$ is an isotropic vector subspace unless
${\cal S}(\beta|_{N_1\times N_1})$ is an isotropic vector subspace unless ![]() $\beta|_{N_1\times N_1}=0$. In the former case, we have from Proposition 9 applied to
$\beta|_{N_1\times N_1}=0$. In the former case, we have from Proposition 9 applied to ![]() $\beta|_{N_1\times N_1}$ that there is a non-zero light-like vector
$\beta|_{N_1\times N_1}$ that there is a non-zero light-like vector ![]() $z\in\mathbb{L}^p$, such that
$z\in\mathbb{L}^p$, such that
 \begin{equation*}
{\cal S}(\beta|_{N_1\times N_1})=
{\cal S}(\beta|_{N_1\times N_1})\cap({\cal S}(\beta|_{N_1\times N_1}))^\perp
=\textrm{span}\{z\}\oplus\textrm{span}\{z\}.
\end{equation*}
\begin{equation*}
{\cal S}(\beta|_{N_1\times N_1})=
{\cal S}(\beta|_{N_1\times N_1})\cap({\cal S}(\beta|_{N_1\times N_1}))^\perp
=\textrm{span}\{z\}\oplus\textrm{span}\{z\}.
\end{equation*} Since ![]() $N_1\subset N(X)$, we obtain from Equation (8) that
$N_1\subset N(X)$, we obtain from Equation (8) that ![]() $(z,0)\in B_X(V)$ and, similarly, we have that
$(z,0)\in B_X(V)$ and, similarly, we have that ![]() $(z,0)\in B_Y(V)$. Then Lemma 10 yields
$(z,0)\in B_Y(V)$. Then Lemma 10 yields ![]() $z\in\textrm{span}\{v\}\cap\textrm{span}\{w\}=0$, which is not possible. We conclude that
$z\in\textrm{span}\{v\}\cap\textrm{span}\{w\}=0$, which is not possible. We conclude that ![]() $\beta|_{N_1\times N_1}=0$.
$\beta|_{N_1\times N_1}=0$.
If ![]() $\beta|_{V\times N_1}\neq 0$, there are vectors
$\beta|_{V\times N_1}\neq 0$, there are vectors ![]() $Z\in V^{2n}$ and
$Z\in V^{2n}$ and ![]() $T\in N_1$ such that
$T\in N_1$ such that ![]() $\beta(Z,T)=(\xi,\eta)\neq 0$. Then Equation (5) and the flatness of β give
$\beta(Z,T)=(\xi,\eta)\neq 0$. Then Equation (5) and the flatness of β give
By Equation (1), the vector subspace ![]() ${\cal S}(\beta|_{V\times N_1})$ is isotropic and thus
${\cal S}(\beta|_{V\times N_1})$ is isotropic and thus
Thus, the vectors ![]() $\xi,\eta$ are light-like. Then from Equation (1) and the second part of Lemma 10, we obtain that
$\xi,\eta$ are light-like. Then from Equation (1) and the second part of Lemma 10, we obtain that ![]() $\xi,\eta\in\textrm{span}\{v\}\cap\textrm{span}\{w\}=0$, and this is a contradiction. Then
$\xi,\eta\in\textrm{span}\{v\}\cap\textrm{span}\{w\}=0$, and this is a contradiction. Then ![]() $\beta|_{V\times N_1}=0$ as wished.
$\beta|_{V\times N_1}=0$ as wished.
1.3. A special flat bilinear form
Throughout this section, ![]() $V^{2n}$ is endowed with a positive definite inner product denoted by
$V^{2n}$ is endowed with a positive definite inner product denoted by ![]() $(,)$ with respect to which
$(,)$ with respect to which ![]() $J\in Aut(V)$ is an isometry. In addition, we assume that there exists a time-like of unit length vector
$J\in Aut(V)$ is an isometry. In addition, we assume that there exists a time-like of unit length vector ![]() $w\in\mathbb{L}^p$ such that
$w\in\mathbb{L}^p$ such that
for any ![]() $X,Y\in V^{2n}$.
$X,Y\in V^{2n}$.
Under the assumptions above, ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ given by Equation (3) satisfies
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ given by Equation (3) satisfies
In particular, if ![]() $\beta(X,Y)=0$, then
$\beta(X,Y)=0$, then ![]() $(X,Y)=0$ and
$(X,Y)=0$ and
Proposition 12. Let the bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be flat and the vector subspace
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be flat and the vector subspace ![]() ${\cal S}(\beta)$ degenerate. If
${\cal S}(\beta)$ degenerate. If ![]() $v\in U_0^s$ is a light-like vector as in Equation (7), then the plane
$v\in U_0^s$ is a light-like vector as in Equation (7), then the plane ![]() $L=\textrm{span}\{v,w\}\subset\mathbb{L}^p$ is Lorentzian. Moreover, choosing v such that
$L=\textrm{span}\{v,w\}\subset\mathbb{L}^p$ is Lorentzian. Moreover, choosing v such that ![]() $\langle v,w\rangle=-1$ and setting
$\langle v,w\rangle=-1$ and setting ![]() $\beta_1=\pi_{L^\perp\times L^\perp}\circ\beta$, we have
$\beta_1=\pi_{L^\perp\times L^\perp}\circ\beta$, we have
for any ![]() $X,Y\in V^{2n}$. Furthermore, if
$X,Y\in V^{2n}$. Furthermore, if ![]() $s\leq n$, then
$s\leq n$, then
Proof. The plane L is trivially Lorentzian. We choose v such that ![]() $v=u+w$, where u is a space-like unit vector orthogonal to w. Then
$v=u+w$, where u is a space-like unit vector orthogonal to w. Then ![]() $L=\textrm{span}\,\{u ,w\}$.
$L=\textrm{span}\,\{u ,w\}$.
We have from Equation (7) that
for any ![]() $X,Y\in V^{2n}$. Then from Equations (12) and (16), we have
$X,Y\in V^{2n}$. Then from Equations (12) and (16), we have
for any ![]() $X,Y\in V^{2n}$. From Equation (12), we obtain
$X,Y\in V^{2n}$. From Equation (12), we obtain
 \begin{align}
\alpha(X,Y)+\alpha(JX,JY)&=\alpha_{L^\perp}(X,Y)+\alpha_{L^\perp}(JX,JY)
+\langle\alpha(X,Y)+\alpha(JX,JY),u\rangle u\nonumber\\
&\quad-\langle\alpha(X,Y)+\alpha(JX,JY),w\rangle w\nonumber\\
&=\alpha_{L^\perp}(X,Y)+\alpha_{L^\perp}(JX,JY)+2(X,Y)v
\end{align}
\begin{align}
\alpha(X,Y)+\alpha(JX,JY)&=\alpha_{L^\perp}(X,Y)+\alpha_{L^\perp}(JX,JY)
+\langle\alpha(X,Y)+\alpha(JX,JY),u\rangle u\nonumber\\
&\quad-\langle\alpha(X,Y)+\alpha(JX,JY),w\rangle w\nonumber\\
&=\alpha_{L^\perp}(X,Y)+\alpha_{L^\perp}(JX,JY)+2(X,Y)v
\end{align}and then Equation (3) gives Equation (14).
We have seen that v can be chosen so that ![]() $\langle v,w\rangle=-1$ and that Equation (14) holds. From Equations (6) and (7), we obtain that
$\langle v,w\rangle=-1$ and that Equation (14) holds. From Equations (6) and (7), we obtain that ![]() $w\notin U_0^s$. Hence,
$w\notin U_0^s$. Hence, ![]() $\dim(U_0^s+L^\perp)=p-1$. Then from
$\dim(U_0^s+L^\perp)=p-1$. Then from
we have that ![]() $U_1=U_0^s\cap L^\perp$ satisfies
$U_1=U_0^s\cap L^\perp$ satisfies
Hence, ![]() ${\cal S}(\beta_1)=U_1^{s-1}\oplus U_1^{s-1}$ from Equations (6), (7) and (14).
${\cal S}(\beta_1)=U_1^{s-1}\oplus U_1^{s-1}$ from Equations (6), (7) and (14).
From Equation (14), the bilinear form ![]() $\beta_1\colon V^{2n}\times V^{2n}\to L^\perp\oplus L^\perp$ is flat. Let
$\beta_1\colon V^{2n}\times V^{2n}\to L^\perp\oplus L^\perp$ is flat. Let ![]() $X\in RE(\beta_1)$ and set
$X\in RE(\beta_1)$ and set ![]() $N_1(X)=\ker B_{1X}$, where
$N_1(X)=\ker B_{1X}$, where ![]() $B_{1X}Y=\beta_1(X,Y)$. To obtain Equation (15), it suffices to show that
$B_{1X}Y=\beta_1(X,Y)$. To obtain Equation (15), it suffices to show that ![]() $N_1(X)=\mathcal{N}(\beta_1)$, since then
$N_1(X)=\mathcal{N}(\beta_1)$, since then ![]() $\dim\mathcal{N}(\beta_1)=\dim N_1(X)\geq 2n-2\dim U_1$.
$\dim\mathcal{N}(\beta_1)=\dim N_1(X)\geq 2n-2\dim U_1$.
Let ![]() $\beta_1(Y,Z)=(\xi,\eta)$, where
$\beta_1(Y,Z)=(\xi,\eta)$, where ![]() $Y,Z\in N_1(X)$. From Equations (1) and (5), we have
$Y,Z\in N_1(X)$. From Equations (1) and (5), we have
Thus, ![]() $\beta_1|_{N_1(X)\times N_1(X)}=0$, since the inner product induced on U 1 is positive definite. Now let
$\beta_1|_{N_1(X)\times N_1(X)}=0$, since the inner product induced on U 1 is positive definite. Now let ![]() $\beta_1(Y,Z)=(\delta,\zeta)$, where
$\beta_1(Y,Z)=(\delta,\zeta)$, where ![]() $Y\in V^{2n}$ and
$Y\in V^{2n}$ and ![]() $Z\in N_1(X)$. The flatness of β 1 and Equation (5) yield
$Z\in N_1(X)$. The flatness of β 1 and Equation (5) yield
and hence ![]() $\beta_1|_{V\times N_1(X)}=0$.
$\beta_1|_{V\times N_1(X)}=0$.
Proposition 13. Let the bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be flat and the vector subspace
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be flat and the vector subspace ![]() ${\cal S}(\beta)$ degenerate. If
${\cal S}(\beta)$ degenerate. If ![]() $\gamma\colon V^{2n}\times V^{2n}\to W^{p,p}$ is the bilinear form defined by
$\gamma\colon V^{2n}\times V^{2n}\to W^{p,p}$ is the bilinear form defined by
assume that
for any ![]() $X,Y,Z,T\in V^{2n}$. If
$X,Y,Z,T\in V^{2n}$. If ![]() $s\leq n-1$, we have the following:
$s\leq n-1$, we have the following:
(i) For
 $v\in U_0^s$ satisfying Equation (7), we have
(21)
$v\in U_0^s$ satisfying Equation (7), we have
(21) \begin{equation}
\langle\alpha(X,Y),v\rangle=0\quad\textrm{for any}\ X,Y\in V^{2n}.
\end{equation}
\begin{equation}
\langle\alpha(X,Y),v\rangle=0\quad\textrm{for any}\ X,Y\in V^{2n}.
\end{equation}(ii) Choosing
 $v\in U_0^s$ satisfying Equation (7) such that
$v\in U_0^s$ satisfying Equation (7) such that  $\langle v,w\rangle=-1$, then with respect to the Lorentzian plane
$\langle v,w\rangle=-1$, then with respect to the Lorentzian plane  $L=\textrm{span}\{v,w\}$, we have
(22)
$L=\textrm{span}\{v,w\}$, we have
(22) \begin{equation}
\alpha(X,Y)=\alpha_{L^\perp}(X,Y)+(X,Y)v\quad\textrm{for any}\ X,Y\in V^{2n}.
\end{equation}
\begin{equation}
\alpha(X,Y)=\alpha_{L^\perp}(X,Y)+(X,Y)v\quad\textrm{for any}\ X,Y\in V^{2n}.
\end{equation}(iii) There is a J-invariant vector subspace
 $P^{2m}\subset V^{2n}$ with
$P^{2m}\subset V^{2n}$ with  $m\geq n-s+1$ such that for any
$m\geq n-s+1$ such that for any  $S\in P^{2m}$, we have
and
$S\in P^{2m}$, we have
and \begin{equation*}
{\cal K}(S)=\langle\alpha(S,S),\alpha(JS,JS)\rangle-\|\alpha(S,JS)\|^2\leq 0
\end{equation*}where
\begin{equation*}
{\cal K}(S)=\langle\alpha(S,S),\alpha(JS,JS)\rangle-\|\alpha(S,JS)\|^2\leq 0
\end{equation*}where \begin{equation*}
{\cal R}(S)=\sum_{i=1}^{2n}(\langle\alpha(X_i,X_i),\alpha(S,S)\rangle-\|\alpha(X_i,S)\|^2)\leq 0,
\end{equation*}
\begin{equation*}
{\cal R}(S)=\sum_{i=1}^{2n}(\langle\alpha(X_i,X_i),\alpha(S,S)\rangle-\|\alpha(X_i,S)\|^2)\leq 0,
\end{equation*} $\{X_i\}_{1\leq i\leq 2n}$ is an orthonormal basis of
$\{X_i\}_{1\leq i\leq 2n}$ is an orthonormal basis of  $V^{2n}$.
$V^{2n}$.
Proof. (i) It suffices to argue for ![]() $v\in U_0^s$ such that
$v\in U_0^s$ such that ![]() $\langle v,w\rangle=-1$. From Equations (14) and (19), we obtain
$\langle v,w\rangle=-1$. From Equations (14) and (19), we obtain
for any ![]() $S\in\mathcal{N}(\beta_1)$ of unit length and
$S\in\mathcal{N}(\beta_1)$ of unit length and ![]() $X,Y\in V^{2n}$. Since we have from Equations (5) and (14) that
$X,Y\in V^{2n}$. Since we have from Equations (5) and (14) that ![]() $\beta(S,Y)=\beta(Y,S)=0$ for any
$\beta(S,Y)=\beta(Y,S)=0$ for any ![]() $S\in\mathcal{N}(\beta_1)$ and
$S\in\mathcal{N}(\beta_1)$ and ![]() $Y\in\{S,JS\}^\perp$, then Equations (20) and (23) give
$Y\in\{S,JS\}^\perp$, then Equations (20) and (23) give
for any ![]() $X\in V^{2n}$ and
$X\in V^{2n}$ and ![]() $Y\in\{S,JS\}^\perp$, where
$Y\in\{S,JS\}^\perp$, where ![]() $S\in\mathcal{N}(\beta_1)$. Since
$S\in\mathcal{N}(\beta_1)$. Since ![]() $s\leq n-1$, then Equation (15) gives
$s\leq n-1$, then Equation (15) gives ![]() $\dim\mathcal{N}(\beta_1)\geq 4$ and now Equation (21) follows from Equation (24).
$\dim\mathcal{N}(\beta_1)\geq 4$ and now Equation (21) follows from Equation (24).
(ii) From Proposition 12, the plane ![]() $L=\textrm{span}\{v,w\}$ is Lorentzian. There is
$L=\textrm{span}\{v,w\}$ is Lorentzian. There is ![]() $u\perp w$ space-like of unit length such that
$u\perp w$ space-like of unit length such that ![]() $v=u+w$. Hence, Equations (11) and (21) give
$v=u+w$. Hence, Equations (11) and (21) give ![]() $\langle\alpha(X,Y),u\rangle=(X,Y)$. Now since
$\langle\alpha(X,Y),u\rangle=(X,Y)$. Now since
then Equation (22) follows from Equation (11).
(iii) We choose ![]() $v\in U_0^s$ satisfying Equation (7) such that
$v\in U_0^s$ satisfying Equation (7) such that ![]() $\langle v,w\rangle=-1$. From Equation (22), we have
$\langle v,w\rangle=-1$. From Equation (22), we have
Set ![]() $P^{2m}=\mathcal{N}(\beta_1)$. From Equation (15), we have
$P^{2m}=\mathcal{N}(\beta_1)$. From Equation (15), we have ![]() $2m=\dim\mathcal{N}(\beta_1)\geq 2n-2s+2$. It follows from Equation (14) that
$2m=\dim\mathcal{N}(\beta_1)\geq 2n-2s+2$. It follows from Equation (14) that ![]() $\beta(Z,S)=2((Z,S)v,(Z,JS)v)$ for any
$\beta(Z,S)=2((Z,S)v,(Z,JS)v)$ for any ![]() $S\in P^{2m}$ and
$S\in P^{2m}$ and ![]() $Z\in V^{2n}$. Then Equation (20) gives
$Z\in V^{2n}$. Then Equation (20) gives
for any ![]() $S\in P^{2m}$ and
$S\in P^{2m}$ and ![]() $X,Y,Z\in V^{2n}$. Thus, the vector subspaces
$X,Y,Z\in V^{2n}$. Thus, the vector subspaces ![]() ${\cal S}(\gamma|_{V\times P})$ and
${\cal S}(\gamma|_{V\times P})$ and ![]() ${\cal S}(\beta)$ are orthogonal. From Equation (18), we have
${\cal S}(\beta)$ are orthogonal. From Equation (18), we have
where ![]() $U_1^{s-1}=U_0^s\cap L^\perp$. Then by Equation (6), the vector subspaces
$U_1^{s-1}=U_0^s\cap L^\perp$. Then by Equation (6), the vector subspaces ![]() ${\cal S}(\gamma|_{V\times P})$ and
${\cal S}(\gamma|_{V\times P})$ and ![]() $U_1^{s-1}\oplus U_1^{s-1}$ are orthogonal and therefore
$U_1^{s-1}\oplus U_1^{s-1}$ are orthogonal and therefore
for any ![]() $X\in V^{2n}$,
$X\in V^{2n}$, ![]() $S\in P^{2m}$ and
$S\in P^{2m}$ and ![]() $\xi\in U^{s-1}_1$. Since
$\xi\in U^{s-1}_1$. Since ![]() $U_1^{s-1}\subset L^\perp$, then
$U_1^{s-1}\subset L^\perp$, then
for any ![]() $X\in V^{2n}$ and
$X\in V^{2n}$ and ![]() $S\in P^{2m}$.
$S\in P^{2m}$.
Let  $U_2^{p-s-1}\subset L^\perp$ be given by the orthogonal decomposition
$U_2^{p-s-1}\subset L^\perp$ be given by the orthogonal decomposition  $\mathbb{L}^p=U_1^{s-1}\oplus U_2^{p-s-1}\oplus L$. By Equations (6) and (25), we have
$\mathbb{L}^p=U_1^{s-1}\oplus U_2^{p-s-1}\oplus L$. By Equations (6) and (25), we have
for any ![]() $X,Y\in V^{2n}$ and
$X,Y\in V^{2n}$ and  $\xi_2\in U_2^{p-s-1}$. Thus,
$\xi_2\in U_2^{p-s-1}$. Thus,
for any ![]() $X,Y\in V^{2n}$.
$X,Y\in V^{2n}$.
From Equations (22), (26) and (27) and since the inner product induced on  $U_2^{p-s-1}$ is positive definite, we have
$U_2^{p-s-1}$ is positive definite, we have
 \begin{equation*}
{\cal K}(S)=\langle\alpha_{U_2}(S,S),\alpha_{U_2}(JS,JS)\rangle-\|\alpha_{U_2}(S,JS)\|^2
=-\|\alpha_{U_2}(S,S)\|^2-\|\alpha_{U_2}(S,JS)\|^2\leq 0
\end{equation*}
\begin{equation*}
{\cal K}(S)=\langle\alpha_{U_2}(S,S),\alpha_{U_2}(JS,JS)\rangle-\|\alpha_{U_2}(S,JS)\|^2
=-\|\alpha_{U_2}(S,S)\|^2-\|\alpha_{U_2}(S,JS)\|^2\leq 0
\end{equation*}for any ![]() $S\in P^{2m}$. Also,
$S\in P^{2m}$. Also,
 \begin{align*}
{\cal R}(S)&=\sum_{i=1}^n(\langle\alpha_{U_2}(Y_i,Y_i),\alpha_{U_2}(S,S)\rangle
-\|\alpha_{U_2}(Y_i,S)\|^2+\langle\alpha_{U_2}(JY_i,JY_i),\alpha_{U_2}(S,S)\rangle\\
&\hspace{5ex}-\|\alpha_{U_2}(JY_i,S)\|^2)\\
&=-\sum_{i=1}^n(\|\alpha_{U_2}(Y_i,S)\|^2
+\|\alpha_{U_2}(JY_i,S)\|^2)\leq 0
\end{align*}
\begin{align*}
{\cal R}(S)&=\sum_{i=1}^n(\langle\alpha_{U_2}(Y_i,Y_i),\alpha_{U_2}(S,S)\rangle
-\|\alpha_{U_2}(Y_i,S)\|^2+\langle\alpha_{U_2}(JY_i,JY_i),\alpha_{U_2}(S,S)\rangle\\
&\hspace{5ex}-\|\alpha_{U_2}(JY_i,S)\|^2)\\
&=-\sum_{i=1}^n(\|\alpha_{U_2}(Y_i,S)\|^2
+\|\alpha_{U_2}(JY_i,S)\|^2)\leq 0
\end{align*}for any ![]() $S\in P^{2m}$ and an orthonormal basis
$S\in P^{2m}$ and an orthonormal basis ![]() $\{Y_j,JY_j\}_{1\leq j\leq n}$.
$\{Y_j,JY_j\}_{1\leq j\leq n}$.
Lemma 14. Let the bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be flat. Assume that the vector subspace
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$ be flat. Assume that the vector subspace ![]() ${\cal S}(\beta)$ is non-degenerate. If
${\cal S}(\beta)$ is non-degenerate. If ![]() $Z\in V^{2n}$ satisfies
$Z\in V^{2n}$ satisfies ![]() $\dim N(Z)=2n-2$, then
$\dim N(Z)=2n-2$, then ![]() $B_ZZ=(\xi,0)\neq 0$, the vector subspace
$B_ZZ=(\xi,0)\neq 0$, the vector subspace ![]() $B_Z(V)=\textrm{span}\{\xi\}\oplus\textrm{span}\{\xi\}$ is non-degenerate and the decomposition
$B_Z(V)=\textrm{span}\{\xi\}\oplus\textrm{span}\{\xi\}$ is non-degenerate and the decomposition
is orthogonal.
Proof. We have ![]() $0\neq B_ZZ=(\xi,0)$ and
$0\neq B_ZZ=(\xi,0)$ and ![]() $B_ZJZ=-(0,\xi)$. If
$B_ZJZ=-(0,\xi)$. If ![]() $Y\in N(Z)$, then
$Y\in N(Z)$, then
and thus ![]() $N(Z)\subset\{Z,JZ\}^\perp$. Since
$N(Z)\subset\{Z,JZ\}^\perp$. Since ![]() $\dim N(Z)=2n-2$, then
$\dim N(Z)=2n-2$, then ![]() $N(Z)=\{Z,JZ\}^\perp$ and
$N(Z)=\{Z,JZ\}^\perp$ and ![]() $\dim B_Z(V)=2$ gives
$\dim B_Z(V)=2$ gives ![]() $B_Z(V)=\textrm{span}\{\xi\}\oplus\textrm{span}\{\xi\}$. From Equations (4) and (5), we obtain
$B_Z(V)=\textrm{span}\{\xi\}\oplus\textrm{span}\{\xi\}$. From Equations (4) and (5), we obtain
The flatness of β gives
for any ![]() $S,T\in N(Z)$ and
$S,T\in N(Z)$ and ![]() $Y\in V^{2n}$. Hence, the decomposition (28) is orthogonal and thus the vector subspace
$Y\in V^{2n}$. Hence, the decomposition (28) is orthogonal and thus the vector subspace ![]() $B_Z(V)$ is non-degenerate.
$B_Z(V)$ is non-degenerate.
The following is the fundamental result obtained in this first section, although it is not needed for the proof of Theorem 3. We observe that Lemma 7 in [Reference Florit, Hui and Zheng7] is a Riemannian version of the result. For an alternative version of the Riemannian result in the spirit of this paper, see Proposition 2.6 in [Reference Chion and Dajczer2].
Proposition 15. Let the bilinear form ![]() $\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$,
$\beta\colon V^{2n}\times V^{2n}\to W^{p,p}$, ![]() $s\leq n$, be flat. Assume that the subspace
$s\leq n$, be flat. Assume that the subspace ![]() ${\cal S}(\beta)$ is non-degenerate and Equation (20) holds. For
${\cal S}(\beta)$ is non-degenerate and Equation (20) holds. For ![]() $p\geq 4$, assume further that there is no non-trivial J-invariant vector subspace
$p\geq 4$, assume further that there is no non-trivial J-invariant vector subspace ![]() $V_1\subset V^{2n}$ such that the subspace
$V_1\subset V^{2n}$ such that the subspace ![]() ${\cal S}(\beta|_{V_1\times V_1})$ is degenerate and that
${\cal S}(\beta|_{V_1\times V_1})$ is degenerate and that ![]() $\dim{\cal S}(\beta|_{V_1\times V_1})\leq\dim V_1-2$. Then s = n, and there is an orthogonal basis
$\dim{\cal S}(\beta|_{V_1\times V_1})\leq\dim V_1-2$. Then s = n, and there is an orthogonal basis ![]() $\{X_i,JX_i\}_{1\leq i\leq n}$ of
$\{X_i,JX_i\}_{1\leq i\leq n}$ of ![]() $V^{2n}$ such that
$V^{2n}$ such that
(i)
 $\beta(Y_i,Y_j)=0\ {if}\ i\neq j
\ {and}\ Y_k\in {span}\{X_k,JX_k\}$ for k=i,j.
$\beta(Y_i,Y_j)=0\ {if}\ i\neq j
\ {and}\ Y_k\in {span}\{X_k,JX_k\}$ for k=i,j.(ii) The vectors
 $\{\beta(X_j,X_j),\beta(X_j,JX_j)\}_{1\leq j\leq n}$ form an orthonormal basis of
$\{\beta(X_j,X_j),\beta(X_j,JX_j)\}_{1\leq j\leq n}$ form an orthonormal basis of  ${\cal S}(\beta)$.
${\cal S}(\beta)$.
Proof. Since ![]() $\mathcal{N}(\beta)=0$, then by Proposition 11, we have that s = n. Moreover, we have that
$\mathcal{N}(\beta)=0$, then by Proposition 11, we have that s = n. Moreover, we have that ![]() $B_X\colon V^{2n}\to U_0^n\oplus U_0^n\subset W^{p,p}$ is an isomorphism for any
$B_X\colon V^{2n}\to U_0^n\oplus U_0^n\subset W^{p,p}$ is an isomorphism for any ![]() $X\in RE(\beta)$.
$X\in RE(\beta)$.
Fact 1. If ![]() $n\geq 2$, then there are non-zero vectors
$n\geq 2$, then there are non-zero vectors ![]() $X,Y\in V^{2n}$, satisfying
$X,Y\in V^{2n}$, satisfying ![]() $\beta(X,Y)=0$.
$\beta(X,Y)=0$.
We have that ![]() ${\rm RE}(\beta)$ is open and dense in
${\rm RE}(\beta)$ is open and dense in ![]() $V^{2n}$ and that
$V^{2n}$ and that ![]() $B_X\colon V^{2n}\to U_0^n\oplus U_0^n$ is an isomorphism for any
$B_X\colon V^{2n}\to U_0^n\oplus U_0^n$ is an isomorphism for any ![]() $X\in {\rm RE}(\beta)$. Hence, there is a basis
$X\in {\rm RE}(\beta)$. Hence, there is a basis ![]() $Z_1,\ldots,Z_{2n}$ of
$Z_1,\ldots,Z_{2n}$ of ![]() $V^{2n}$ with
$V^{2n}$ with ![]() $Z_2\not\in\textrm{span}\,\{Z_1,JZ_1\}$, such that
$Z_2\not\in\textrm{span}\,\{Z_1,JZ_1\}$, such that ![]() $\{\beta(Z_1,Z_j)\}_{1\leq j\leq 2n}$ and
$\{\beta(Z_1,Z_j)\}_{1\leq j\leq 2n}$ and ![]() $\{\beta(Z_2,Z_j)\}_{1\leq j\leq 2n}$ are both basis of
$\{\beta(Z_2,Z_j)\}_{1\leq j\leq 2n}$ are both basis of ![]() $U_0^n\oplus U_0^n$. Let
$U_0^n\oplus U_0^n$. Let ![]() $A=(a_{ij})$ be the
$A=(a_{ij})$ be the ![]() $2n\times 2n$ matrix given by
$2n\times 2n$ matrix given by
 \begin{equation*}
\beta(Z_2,Z_j)=\sum_{r=1}^{2n}a_{rj}\beta(Z_1,Z_r).
\end{equation*}
\begin{equation*}
\beta(Z_2,Z_j)=\sum_{r=1}^{2n}a_{rj}\beta(Z_1,Z_r).
\end{equation*} Let ![]() $\lambda\in\mathbb{C}$ be an eigenvalue of A with corresponding eigenvector
$\lambda\in\mathbb{C}$ be an eigenvalue of A with corresponding eigenvector ![]() $(v^1,\ldots,v^{2n})\in\mathbb{C}^{2n}$. Extending β linearly from
$(v^1,\ldots,v^{2n})\in\mathbb{C}^{2n}$. Extending β linearly from ![]() $V^{2n}\otimes\mathbb{C}$ to
$V^{2n}\otimes\mathbb{C}$ to ![]() $W^{p,p}\otimes\mathbb{C}$, we have
$W^{p,p}\otimes\mathbb{C}$, we have
 \begin{equation*}
\sum_{j=1}^{2n}v^j\beta(Z_2,Z_j)
=\lambda\sum_{j=1}^{2n}v^j\beta(Z_1,Z_j).
\end{equation*}
\begin{equation*}
\sum_{j=1}^{2n}v^j\beta(Z_2,Z_j)
=\lambda\sum_{j=1}^{2n}v^j\beta(Z_1,Z_j).
\end{equation*} Hence, ![]() $\beta(S,T)=0$, where
$\beta(S,T)=0$, where ![]() $S=Z_2-\lambda Z_1$ and
$S=Z_2-\lambda Z_1$ and  $T=\sum_{j=1}^{2n}v^jZ_j$. Setting
$T=\sum_{j=1}^{2n}v^jZ_j$. Setting ![]() $S=S_1+{\rm i}S_2$ and
$S=S_1+{\rm i}S_2$ and ![]() $T=T_1+{\rm i}T_2$, it follows that
$T=T_1+{\rm i}T_2$, it follows that
Then, if ![]() $X=S_1-JS_2$ and
$X=S_1-JS_2$ and ![]() $Y=T_1+JT_2$, we obtain using Equations (4) and (5) that
$Y=T_1+JT_2$, we obtain using Equations (4) and (5) that
 \begin{align*}
\beta(X,Y)
&=\beta(S_1,T_1)+\beta(S_1,JT_2)-\beta(JS_2,T_1)-\beta(JS_2,JT_2)\\
&=\beta(S_1,T_1)+\beta(S_1,JT_2)+\beta(S_2,JT_1)-\beta(S_2,T_2)=0.
\end{align*}
\begin{align*}
\beta(X,Y)
&=\beta(S_1,T_1)+\beta(S_1,JT_2)-\beta(JS_2,T_1)-\beta(JS_2,JT_2)\\
&=\beta(S_1,T_1)+\beta(S_1,JT_2)+\beta(S_2,JT_1)-\beta(S_2,T_2)=0.
\end{align*} Similarly, we obtain ![]() $\beta(X^{\prime},Y^{\prime})=0$ for
$\beta(X^{\prime},Y^{\prime})=0$ for ![]() $X^{\prime}=S_1+JS_2$ and
$X^{\prime}=S_1+JS_2$ and ![]() $Y^{\prime}=T_1-JT_2$. The vectors X and Xʹ are both non-zero. For instance, if X = 0, then
$Y^{\prime}=T_1-JT_2$. The vectors X and Xʹ are both non-zero. For instance, if X = 0, then
Thus, ![]() $JS_2=Z_2-\text{Re}(\lambda)Z_1$ and
$JS_2=Z_2-\text{Re}(\lambda)Z_1$ and ![]() $S_2=-\text{Im}(\lambda)Z_1$. But then
$S_2=-\text{Im}(\lambda)Z_1$. But then ![]() $Z_2\in\textrm{span}\{Z_1,JZ_1\}$, and this is a contradiction. Finally, if we have that
$Z_2\in\textrm{span}\{Z_1,JZ_1\}$, and this is a contradiction. Finally, if we have that ![]() $Y=Y^{\prime}=0$, then T = 0, which is also a contradiction.
$Y=Y^{\prime}=0$, then T = 0, which is also a contradiction.
Fact 2. There exists a vector ![]() $Z_0\in V^{2n}$ satisfying
$Z_0\in V^{2n}$ satisfying ![]() $\dim N(Z_0)=2n-2$.
$\dim N(Z_0)=2n-2$.
This Fact holds for n = 1. In fact, if ![]() $0\neq X\in V^2$, then
$0\neq X\in V^2$, then ![]() $\beta(X,X)$ and
$\beta(X,X)$ and ![]() $\beta(X,JX)$ are linearly independent and hence
$\beta(X,JX)$ are linearly independent and hence ![]() $N(X)=0$.
$N(X)=0$.
We argue for ![]() $n\geq 2$. By Fact 1, there are non-zero vectors
$n\geq 2$. By Fact 1, there are non-zero vectors ![]() $X,Y\in V^{2n}$ such that
$X,Y\in V^{2n}$ such that ![]() $\beta(X,Y)=0$. From Equation (5), we have that
$\beta(X,Y)=0$. From Equation (5), we have that ![]() $\dim B_XV=2r$, where
$\dim B_XV=2r$, where ![]() $1\leq r\leq n-1$ since
$1\leq r\leq n-1$ since ![]() $B_XY=0$ and
$B_XY=0$ and ![]() $X\notin N(X)$. Thus,
$X\notin N(X)$. Thus, ![]() $\dim N(X)=2n-2r$. Moreover, we may assume that
$\dim N(X)=2n-2r$. Moreover, we may assume that ![]() $2\leq r\leq n-1$ since Fact 2 holds when r = 1 by taking
$2\leq r\leq n-1$ since Fact 2 holds when r = 1 by taking ![]() $Z_0=X$. Therefore, we assume that
$Z_0=X$. Therefore, we assume that ![]() $n\geq 3$.
$n\geq 3$.
Set ![]() $U_1^t=\pi_1(B_X(V))$. We claim that t = r and that
$U_1^t=\pi_1(B_X(V))$. We claim that t = r and that
In order to prove the claim, we first show that
which, in particular, yields ![]() $t\geq r$. If
$t\geq r$. If ![]() $\beta(X,Z_1)=(\xi,\eta)$ and
$\beta(X,Z_1)=(\xi,\eta)$ and ![]() $\beta(Z_2,X)=(\zeta,\delta)$, then Equation (5) gives
$\beta(Z_2,X)=(\zeta,\delta)$, then Equation (5) gives ![]() $\beta(X,JZ_1)=(\eta,-\xi)$ and
$\beta(X,JZ_1)=(\eta,-\xi)$ and ![]() $\beta(X,JZ_2)=-(\delta,\zeta)$. Hence,
$\beta(X,JZ_2)=-(\delta,\zeta)$. Hence, ![]() $\xi,\zeta,\eta,\delta\in U_1^t$ and thus
$\xi,\zeta,\eta,\delta\in U_1^t$ and thus ![]() $(\xi,\eta),(\zeta,\delta)\in U_1^t\oplus U_1^t$. Now let
$(\xi,\eta),(\zeta,\delta)\in U_1^t\oplus U_1^t$. Now let ![]() $(\xi_1,\xi_2)\in U_1^t\oplus U_1^t$. Then there are
$(\xi_1,\xi_2)\in U_1^t\oplus U_1^t$. Then there are ![]() $Z_1,Z_2\in V^{2p}$ such that
$Z_1,Z_2\in V^{2p}$ such that ![]() $\beta(X,Z_i)=(\xi_i,\eta_i)$,
$\beta(X,Z_i)=(\xi_i,\eta_i)$, ![]() $i=1,2$. Using Equation (5), we obtain
$i=1,2$. Using Equation (5), we obtain
 \begin{equation*}
(\xi_1,\xi_2)=\frac{1}{2}\left(\beta(X,Z_1-JZ_2)+\beta(Z_1+JZ_2,X)\right),
\end{equation*}
\begin{equation*}
(\xi_1,\xi_2)=\frac{1}{2}\left(\beta(X,Z_1-JZ_2)+\beta(Z_1+JZ_2,X)\right),
\end{equation*}and Equation (30) has been proved.
We show that t = r. In the process and for later use, we also prove that
where  $\bar\beta=\beta|_{N(X)\times N(X)}$ and
$\bar\beta=\beta|_{N(X)\times N(X)}$ and ![]() $U_2^{n-r}=U_0^n\cap(U_1^r)^\perp$. The flatness of β gives
$U_2^{n-r}=U_0^n\cap(U_1^r)^\perp$. The flatness of β gives
for any ![]() $S,T\in N(X)$ and
$S,T\in N(X)$ and ![]() $Z\in V^{2n}$. From Equation (5), we have
$Z\in V^{2n}$. From Equation (5), we have ![]() $\beta(S,X)=0$ and thus
$\beta(S,X)=0$ and thus
for any ![]() $S,T\in N(X)$ and
$S,T\in N(X)$ and ![]() $Z\in V^{2n}$. Since
$Z\in V^{2n}$. Since ![]() ${\cal S}(\bar\beta)\subset{\cal S}(\beta)$, then from Equation (30), we have
${\cal S}(\bar\beta)\subset{\cal S}(\beta)$, then from Equation (30), we have
Suppose that the vector subspace ![]() ${\cal S}(\bar\beta)$ is non-degenerate. Since
${\cal S}(\bar\beta)$ is non-degenerate. Since ![]() $\dim N(X)=2n-2r$, we have from Equations (9) and (32) that
$\dim N(X)=2n-2r$, we have from Equations (9) and (32) that
Since ![]() $\mathcal{N}(\bar\beta)=0$ because
$\mathcal{N}(\bar\beta)=0$ because ![]() $\beta(Z,Z)\neq 0$ if Z ≠ 0 and
$\beta(Z,Z)\neq 0$ if Z ≠ 0 and ![]() $t\geq r$, then t = r and
$t\geq r$, then t = r and ![]() $\dim{\cal S}(\bar\beta)=2n-2r$. Suppose now that the vector subspace
$\dim{\cal S}(\bar\beta)=2n-2r$. Suppose now that the vector subspace ![]() ${\cal S}(\bar\beta)$ is degenerate. If n = 3, then r = 2. Since
${\cal S}(\bar\beta)$ is degenerate. If n = 3, then r = 2. Since ![]() ${\cal S}(\bar\beta)\neq 0$, then also t = 2 and Equation (31) follows. Then let
${\cal S}(\bar\beta)\neq 0$, then also t = 2 and Equation (31) follows. Then let ![]() $n\geq 4$. We have from Equation (32) that
$n\geq 4$. We have from Equation (32) that
and the assumption in the statement yields that t = r and ![]() $\dim{\cal S}(\bar\beta)=2n-2r$. Having proved that
$\dim{\cal S}(\bar\beta)=2n-2r$. Having proved that ![]() $\dim{\cal S}(\bar\beta)=2n-2r$ holds in both cases, then Equation (31) follows from Equation (6). Finally, since t = r, then Equation (29) follows from Equation (30) using Equation (5), and thus the claim has been proved.
$\dim{\cal S}(\bar\beta)=2n-2r$ holds in both cases, then Equation (31) follows from Equation (6). Finally, since t = r, then Equation (29) follows from Equation (30) using Equation (5), and thus the claim has been proved.
We now claim that in fact the vector subspace ![]() ${\cal S}(\bar\beta)$ is non-degenerate. Assuming otherwise, we have from Equation (14) that
${\cal S}(\bar\beta)$ is non-degenerate. Assuming otherwise, we have from Equation (14) that
for any ![]() $S,T\in N(X)$, where the light-like vector
$S,T\in N(X)$, where the light-like vector ![]() $v\in U_0^n$ satisfies
$v\in U_0^n$ satisfies ![]() $\langle v,w\rangle=-1$ and
$\langle v,w\rangle=-1$ and
Since ![]() $\beta(R,X)=0$ for
$\beta(R,X)=0$ for ![]() $R\in N(X)$ by Equation (5), then the flatness of β gives
$R\in N(X)$ by Equation (5), then the flatness of β gives
for any ![]() $Y,Z\in V^{2n}$ and
$Y,Z\in V^{2n}$ and ![]() $R\in N(X)$. Therefore, for
$R\in N(X)$. Therefore, for ![]() $R\in N(X)$, the vector subspaces
$R\in N(X)$, the vector subspaces ![]() $B_R(V)$ and
$B_R(V)$ and ![]() $\{\beta(Y,X)\colon Y\in V^{2p}\}$ are orthogonal. From Equations (29) and (31), we obtain that
$\{\beta(Y,X)\colon Y\in V^{2p}\}$ are orthogonal. From Equations (29) and (31), we obtain that ![]() $B_R(V)\subset U_2^{n-r}\oplus U_2^{n-r}
={\cal S}(\bar\beta)$ if
$B_R(V)\subset U_2^{n-r}\oplus U_2^{n-r}
={\cal S}(\bar\beta)$ if ![]() $R\in N(X)$. By Equation (15), the vector subspace
$R\in N(X)$. By Equation (15), the vector subspace ![]() $N_0=\mathcal{N}(\bar\beta_1)\subset N(X)$ is non-zero, and from Equations (5) and (33), we have
$N_0=\mathcal{N}(\bar\beta_1)\subset N(X)$ is non-zero, and from Equations (5) and (33), we have ![]() $B_S(N(X))=\textrm{span}\{v\}\oplus\textrm{span}\{v\}$ for any
$B_S(N(X))=\textrm{span}\{v\}\oplus\textrm{span}\{v\}$ for any ![]() $S\in N_0$. Then from Equation (34) and the flatness of β, it follows that
$S\in N_0$. Then from Equation (34) and the flatness of β, it follows that
for any ![]() $S\in N_0$,
$S\in N_0$, ![]() $Y\in V^{2n}$ and
$Y\in V^{2n}$ and ![]() $R,T\in N(X)$. Hence,
$R,T\in N(X)$. Hence, ![]() $B_S(V)\subset{\cal S}(\bar\beta)\cap({\cal S}(\bar\beta))^\perp$ for any
$B_S(V)\subset{\cal S}(\bar\beta)\cap({\cal S}(\bar\beta))^\perp$ for any ![]() $S\in N_0$. Then from Equations (33) and (34), it follows that
$S\in N_0$. Then from Equations (33) and (34), it follows that ![]() $B_S(V)=\textrm{span}\{v\}\oplus\textrm{span}\{v\}$ for any
$B_S(V)=\textrm{span}\{v\}\oplus\textrm{span}\{v\}$ for any ![]() $S\in N_0$. Since
$S\in N_0$. Since ![]() $\dim N(S)=2n-2$, then by Lemma 14, the subspace
$\dim N(S)=2n-2$, then by Lemma 14, the subspace ![]() $B_S(V)$ should be non-degenerate. This is a contradiction that proves the claim.
$B_S(V)$ should be non-degenerate. This is a contradiction that proves the claim.
If ![]() $Z_0\in N(X)$, then Equation (5) gives that also
$Z_0\in N(X)$, then Equation (5) gives that also ![]() $\beta(Z_0,X)=0$. The flatness of β yields
$\beta(Z_0,X)=0$. The flatness of β yields
for any ![]() $Y,Z\in V^{2n}$. Then the second equality in Equation (29) gives
$Y,Z\in V^{2n}$. Then the second equality in Equation (29) gives ![]() $B_{Z_0}(V)\subset U_2^{n-r}\oplus U_2^{n-r}$. If
$B_{Z_0}(V)\subset U_2^{n-r}\oplus U_2^{n-r}$. If ![]() $r=n-1$, then Z 0 satisfies
$r=n-1$, then Z 0 satisfies ![]() $\dim\ker B_{Z_0}=2n-2$ as required. Hence, we assume that
$\dim\ker B_{Z_0}=2n-2$ as required. Hence, we assume that ![]() $r\leq n-2$, and thus
$r\leq n-2$, and thus ![]() $n\geq 4$ since
$n\geq 4$ since ![]() $r\geq 2$.
$r\geq 2$.
We conclude the proof of Fact 2 arguing by induction. Assume that it is true for any dimension until n − 1. We have seen that ![]() $\dim N(X)=2n-2r$ with
$\dim N(X)=2n-2r$ with ![]() $2\leq r\leq n-2$. Thus, the assumption of the induction applies to
$2\leq r\leq n-2$. Thus, the assumption of the induction applies to ![]() $\bar\beta\colon N(X)\times N(X)\to U_2^{n-r}\oplus U_2^{n-r}\subset W^{p,p}$ since the vector subspace
$\bar\beta\colon N(X)\times N(X)\to U_2^{n-r}\oplus U_2^{n-r}\subset W^{p,p}$ since the vector subspace ![]() ${\cal S}(\bar\beta)=U_2^{n-r}\oplus U_2^{n-r}$ is non-degenerate. Hence, there is
${\cal S}(\bar\beta)=U_2^{n-r}\oplus U_2^{n-r}$ is non-degenerate. Hence, there is ![]() $Z_0\in N(X)$ such that
$Z_0\in N(X)$ such that  $\dim\ker\bar{B}_{Z_0}=2n-2r-2$. Then Lemma 14 applies, and by Equations (28) and (31), we have
$\dim\ker\bar{B}_{Z_0}=2n-2r-2$. Then Lemma 14 applies, and by Equations (28) and (31), we have
 \begin{equation*}
U_2^{n-r}\oplus U_2^{n-r}
=\bar\beta_{Z_0}(N(X))\oplus{\cal S}\left(\bar\beta|_{\bar{N}(Z_0)\times\bar{N}(Z_0)}\right),
\end{equation*}
\begin{equation*}
U_2^{n-r}\oplus U_2^{n-r}
=\bar\beta_{Z_0}(N(X))\oplus{\cal S}\left(\bar\beta|_{\bar{N}(Z_0)\times\bar{N}(Z_0)}\right),
\end{equation*}where  $\bar{N}(Z_0)=\ker\bar{B}_{Z_0}$. It follows that
$\bar{N}(Z_0)=\ker\bar{B}_{Z_0}$. It follows that  $\dim{\cal S}(\bar\beta|_{\bar{N}(Z_0)\times\bar{N}(Z_0)})=2n-2r-2$. By the flatness of β, we have
$\dim{\cal S}(\bar\beta|_{\bar{N}(Z_0)\times\bar{N}(Z_0)})=2n-2r-2$. By the flatness of β, we have
for any ![]() $R,T\in\bar{N}(Z_0)$ and
$R,T\in\bar{N}(Z_0)$ and ![]() $Y\in V^{2n}$. Hence, the vector subspaces
$Y\in V^{2n}$. Hence, the vector subspaces  ${\cal S}(\bar\beta|_{\bar{N}(Z_0)\times \bar{N}(Z_0)})$ and
${\cal S}(\bar\beta|_{\bar{N}(Z_0)\times \bar{N}(Z_0)})$ and ![]() $B_{Z_0}(V)$ are orthogonal. Since
$B_{Z_0}(V)$ are orthogonal. Since ![]() $B_{Z_0}(V)\subset U_2^{n-r}\oplus U_2^{n-r}$, then
$B_{Z_0}(V)\subset U_2^{n-r}\oplus U_2^{n-r}$, then ![]() $\dim B_{Z_0}(V)=2$, and hence Fact 2 has been proved.
$\dim B_{Z_0}(V)=2$, and hence Fact 2 has been proved.
We conclude the proof of the proposition by means of a recursive construction. Notice that it suffices to construct an orthogonal basis of ![]() ${\cal S}(\beta)$ since it can be normalized. By Fact 2 and Equation (5), there is
${\cal S}(\beta)$ since it can be normalized. By Fact 2 and Equation (5), there is ![]() $X_1\in V^{2n}$ such that the J-invariant vector subspace
$X_1\in V^{2n}$ such that the J-invariant vector subspace ![]() $N(X_1)$ satisfies
$N(X_1)$ satisfies ![]() $\dim N(X_1)=2n-2$. Moreover,
$\dim N(X_1)=2n-2$. Moreover, ![]() $\beta(X_1,X_1)=(\xi_1,0)\neq 0$ and
$\beta(X_1,X_1)=(\xi_1,0)\neq 0$ and ![]() $\beta(X_1,JX_1)=(0,-\xi_1)$. By Lemma 14, the vector ξ 1 is either space-like or time-like.
$\beta(X_1,JX_1)=(0,-\xi_1)$. By Lemma 14, the vector ξ 1 is either space-like or time-like.
By Lemma 14, the decomposition ![]() ${\cal S}(\beta)=B_{X_1}(V)\oplus{\cal S}(\beta_{N(X_1)\times N(X_1)})$ is orthogonal and the vector subspace
${\cal S}(\beta)=B_{X_1}(V)\oplus{\cal S}(\beta_{N(X_1)\times N(X_1)})$ is orthogonal and the vector subspace ![]() ${\cal S}(\beta_{N(X_1)\times N(X_1)})$ is non-degenerate and has dimension
${\cal S}(\beta_{N(X_1)\times N(X_1)})$ is non-degenerate and has dimension ![]() $2n-2$. By Fact 2, there is
$2n-2$. By Fact 2, there is ![]() $X_2\in N(X_1)$ such that
$X_2\in N(X_1)$ such that ![]() $\dim\ker B_{X_2}\cap N(X_1)=2n-4$. Again, we have that
$\dim\ker B_{X_2}\cap N(X_1)=2n-4$. Again, we have that ![]() $\beta(X_2,X_2)=(\xi_2,0)\neq 0$ and
$\beta(X_2,X_2)=(\xi_2,0)\neq 0$ and ![]() $\beta(X_2,JX_2)=(0,-\xi_2)$, where ξ 2 is either space-like or time-like, and the vectors ξ 1 and ξ 2 are orthogonal. Since
$\beta(X_2,JX_2)=(0,-\xi_2)$, where ξ 2 is either space-like or time-like, and the vectors ξ 1 and ξ 2 are orthogonal. Since ![]() $N(X_1)$ is J-invariant, then
$N(X_1)$ is J-invariant, then
Then we have that ![]() $X_1,JX_1,X_2,JX_2$ are orthogonal. If we have n = 2, then the desired basis is
$X_1,JX_1,X_2,JX_2$ are orthogonal. If we have n = 2, then the desired basis is ![]() $X_1,JX_1,X_2,JX_2$, and if
$X_1,JX_1,X_2,JX_2$, and if ![]() $n\geq 3$, we have to reiterate the construction.
$n\geq 3$, we have to reiterate the construction.
2. The proofs
This section is devoted to provide the proofs of the results stated in the introduction.
Let ![]() $f\colon M^{2n}\to\mathbb{H}^{2n+p}$ be an isometric immersion of a Kaehler manifold. Then let
$f\colon M^{2n}\to\mathbb{H}^{2n+p}$ be an isometric immersion of a Kaehler manifold. Then let ![]() $g=i\circ f\colon M^{2n}\to\mathbb{L}^{2n+p+1}$, where
$g=i\circ f\colon M^{2n}\to\mathbb{L}^{2n+p+1}$, where ![]() $i\colon\mathbb{H}^{2n+p}\to\mathbb{L}^{2n+p+1}$ denotes the inclusion. We have that
$i\colon\mathbb{H}^{2n+p}\to\mathbb{L}^{2n+p+1}$ denotes the inclusion. We have that ![]() $N_gM=i_*N_fM\oplus\textrm{span}\{g\}$ and
$N_gM=i_*N_fM\oplus\textrm{span}\{g\}$ and
for any ![]() $X,Y\in\mathfrak{X}(M)$. At
$X,Y\in\mathfrak{X}(M)$. At ![]() $x\in M^{2n}$, let
$x\in M^{2n}$, let ![]() $\gamma,\beta\colon T_xM\times T_xM\to N_gM(x)\oplus N_gM(x)$ be the bilinear forms defined by
$\gamma,\beta\colon T_xM\times T_xM\to N_gM(x)\oplus N_gM(x)$ be the bilinear forms defined by
and
 \begin{align*}
\beta(X,Y)
&=\gamma(X,Y)+\gamma(JX,JY)\\
&=(\alpha^g(X,Y)+\alpha^g(JX,JY),\alpha^g(X,JY)-\alpha^g(JX,Y)).
\end{align*}
\begin{align*}
\beta(X,Y)
&=\gamma(X,Y)+\gamma(JX,JY)\\
&=(\alpha^g(X,Y)+\alpha^g(JX,JY),\alpha^g(X,JY)-\alpha^g(JX,Y)).
\end{align*}Then since α g verifies the condition (11), it follows that β satisfies Equation (13).
Proposition 16. Let ![]() $N_gM(x)\oplus N_gM(x)$ be endowed with the inner product defined by
$N_gM(x)\oplus N_gM(x)$ be endowed with the inner product defined by
Then the bilinear form β is flat, and we have that
for any ![]() $X,Y,Z,T\in T_xM$.
$X,Y,Z,T\in T_xM$.
Proof. It is well-known that the curvature tensor of a Kaehler manifold ![]() $M^{2n}$ satisfies that
$M^{2n}$ satisfies that ![]() $R(X,Y)JZ=JR(X,Y)Z$ for any
$R(X,Y)JZ=JR(X,Y)Z$ for any ![]() $X,Y,Z\in T_xM$. Then this together with the Gauss equation for g give
$X,Y,Z\in T_xM$. Then this together with the Gauss equation for g give
 \begin{align*}
{\langle\!\langle}&\gamma(X,T),\beta(Z,Y){\rangle\!\rangle}\\
&=\langle\alpha(X,T),\alpha(Z,Y)\rangle+\langle\alpha(X,T),\alpha(JZ,JY)\rangle-\langle\alpha(X,JT),\alpha(Z,JY)\rangle\\
&\quad+\langle\alpha(X,JT),\alpha(JZ,Y)\rangle\\
&=\langle R(X,Z)Y,T\rangle+\langle\alpha(X,Y),\alpha(Z,T)\rangle+\langle R(X,JZ)JY,T\rangle\\
&\quad+\langle\alpha(X,JY),\alpha(JZ,T)\rangle-\langle R(X,Z)JY,JT\rangle-\langle\alpha(X,JY),\alpha(Z,JT)\rangle\\
&\quad +\langle R(X,JZ)Y,JT\rangle+\langle\alpha(X,Y),\alpha(JZ,JT)\rangle\\
&=\langle\alpha(X,Y),\alpha(Z,T)\rangle+\langle\alpha(X,JY),\alpha(JZ,T)\rangle-\langle\alpha(X,JY),\alpha(Z,JT)\rangle\\
&\quad+\langle\alpha(X,Y),\alpha(JZ,JT)\rangle\\
&={\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle},
\end{align*}
\begin{align*}
{\langle\!\langle}&\gamma(X,T),\beta(Z,Y){\rangle\!\rangle}\\
&=\langle\alpha(X,T),\alpha(Z,Y)\rangle+\langle\alpha(X,T),\alpha(JZ,JY)\rangle-\langle\alpha(X,JT),\alpha(Z,JY)\rangle\\
&\quad+\langle\alpha(X,JT),\alpha(JZ,Y)\rangle\\
&=\langle R(X,Z)Y,T\rangle+\langle\alpha(X,Y),\alpha(Z,T)\rangle+\langle R(X,JZ)JY,T\rangle\\
&\quad+\langle\alpha(X,JY),\alpha(JZ,T)\rangle-\langle R(X,Z)JY,JT\rangle-\langle\alpha(X,JY),\alpha(Z,JT)\rangle\\
&\quad +\langle R(X,JZ)Y,JT\rangle+\langle\alpha(X,Y),\alpha(JZ,JT)\rangle\\
&=\langle\alpha(X,Y),\alpha(Z,T)\rangle+\langle\alpha(X,JY),\alpha(JZ,T)\rangle-\langle\alpha(X,JY),\alpha(Z,JT)\rangle\\
&\quad+\langle\alpha(X,Y),\alpha(JZ,JT)\rangle\\
&={\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle},
\end{align*}which proves Equation (35). Using Equations (4) and (35), we have
 \begin{align*}
&{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle}={\langle\!\langle}\gamma(JX,T),\beta(Z,JY){\rangle\!\rangle}=
-{\langle\!\langle}\gamma(JX,T),\beta(JZ,Y){\rangle\!\rangle}\\
&=-{\langle\!\langle}\gamma(JX,Y),\beta(JZ,T){\rangle\!\rangle}={\langle\!\langle}\gamma(JX,Y),\beta(Z,JT){\rangle\!\rangle}
={\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle}.
\end{align*}
\begin{align*}
&{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle}={\langle\!\langle}\gamma(JX,T),\beta(Z,JY){\rangle\!\rangle}=
-{\langle\!\langle}\gamma(JX,T),\beta(JZ,Y){\rangle\!\rangle}\\
&=-{\langle\!\langle}\gamma(JX,Y),\beta(JZ,T){\rangle\!\rangle}={\langle\!\langle}\gamma(JX,Y),\beta(Z,JT){\rangle\!\rangle}
={\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle}.
\end{align*}Then
 \begin{align*}
&{\langle\!\langle}\beta(X,Y),\beta(Z,T){\rangle\!\rangle}=
{\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle}\\
&={\langle\!\langle}\gamma(X,T),\beta(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle}
={\langle\!\langle}\beta(X,T),\beta(Z,Y){\rangle\!\rangle},
\end{align*}
\begin{align*}
&{\langle\!\langle}\beta(X,Y),\beta(Z,T){\rangle\!\rangle}=
{\langle\!\langle}\gamma(X,Y),\beta(Z,T){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JY),\beta(Z,T){\rangle\!\rangle}\\
&={\langle\!\langle}\gamma(X,T),\beta(Z,Y){\rangle\!\rangle}+{\langle\!\langle}\gamma(JX,JT),\beta(Z,Y){\rangle\!\rangle}
={\langle\!\langle}\beta(X,T),\beta(Z,Y){\rangle\!\rangle},
\end{align*}and this concludes the proof.
Proof of Theorem 3
Observe that ![]() $s\leq p+1\leq n-1$. At any point
$s\leq p+1\leq n-1$. At any point ![]() $M^{2n}$, the vector subspace
$M^{2n}$, the vector subspace ![]() ${\cal S}(\beta)$ is degenerate. In fact, if we have otherwise, we obtain from Equation (9) that
${\cal S}(\beta)$ is degenerate. In fact, if we have otherwise, we obtain from Equation (9) that ![]() $\dim\mathcal{N}(\beta)\geq 2n-2p-2\geq 2$, which is a contradiction. We have from Proposition 9 that
$\dim\mathcal{N}(\beta)\geq 2n-2p-2\geq 2$, which is a contradiction. We have from Proposition 9 that ![]() $s\leq p$ and the proof now follows from part (iii) of Proposition 13.
$s\leq p$ and the proof now follows from part (iii) of Proposition 13.
Remark 17. For ![]() $f\colon M^{2n}\to\mathbb{H}^{2n+p}$ as in Theorem 3, one can obtain from part (i) of Proposition 13 that there is a smooth unit normal vector field
$f\colon M^{2n}\to\mathbb{H}^{2n+p}$ as in Theorem 3, one can obtain from part (i) of Proposition 13 that there is a smooth unit normal vector field ![]() $\eta\in\Gamma(N_fM)$ such that the second fundamental form satisfies
$\eta\in\Gamma(N_fM)$ such that the second fundamental form satisfies  $A_\eta^f=I$; see below the argument in the proof of Theorem 6. An elementary proof gives that f(M) is contained in a horosphere in
$A_\eta^f=I$; see below the argument in the proof of Theorem 6. An elementary proof gives that f(M) is contained in a horosphere in ![]() $\mathbb{H}^{2n+p}$ if and only if η is parallel in the normal connection.
$\mathbb{H}^{2n+p}$ if and only if η is parallel in the normal connection.
Lemma 18. Let ![]() $f\colon M^{2n}\to\mathbb{H}^{2n+p}$,
$f\colon M^{2n}\to\mathbb{H}^{2n+p}$, ![]() $p\leq n-1$, be an isometric immersion of a Kaehler manifold. At any
$p\leq n-1$, be an isometric immersion of a Kaehler manifold. At any ![]() $y\in M^{2n}$, let
$y\in M^{2n}$, let ![]() $\beta\colon T_yM\times T_yM\to W^{p+1,p+1}=N_gM(y)\oplus N_gM(y)$ be surjective. Moreover, assume that there is an orthogonal basis
$\beta\colon T_yM\times T_yM\to W^{p+1,p+1}=N_gM(y)\oplus N_gM(y)$ be surjective. Moreover, assume that there is an orthogonal basis ![]() $\{X_j,JX_j\}_{1\leq j\leq n}$ of TyM such that parts (i) and (ii) in Proposition 15 hold. Then
$\{X_j,JX_j\}_{1\leq j\leq n}$ of TyM such that parts (i) and (ii) in Proposition 15 hold. Then ![]() $p=n-1$ and f(M) is an open subset of the submanifold given by Example 1.
$p=n-1$ and f(M) is an open subset of the submanifold given by Example 1.
Proof. The vectors ![]() $(\xi_j,0)=\beta(X_j,X_j)\in N_gM(y)\oplus N_gM(y)$,
$(\xi_j,0)=\beta(X_j,X_j)\in N_gM(y)\oplus N_gM(y)$, ![]() $1\leq j\leq n$, in part (ii) of Proposition 15 are the orthonormal basis of
$1\leq j\leq n$, in part (ii) of Proposition 15 are the orthonormal basis of ![]() $W^{p+1,p+1}$. Thus,
$W^{p+1,p+1}$. Thus, ![]() $p=n-1$. Part (i) and Equation (35) give that
$p=n-1$. Part (i) and Equation (35) give that
for any ![]() $Y\in T_yM$. Similarly, we have
$Y\in T_yM$. Similarly, we have ![]() $\langle A_{\xi_i}JX_j,Y\rangle=0$. Hence,
$\langle A_{\xi_i}JX_j,Y\rangle=0$. Hence,
 \begin{equation}
\textrm{span} \{X_i,JX_i\}_{1\leq i\neq j\leq n}\subset\ker A_{\xi_j},
\end{equation}
\begin{equation}
\textrm{span} \{X_i,JX_i\}_{1\leq i\neq j\leq n}\subset\ker A_{\xi_j},
\end{equation}and thus the vector subspaces ![]() $\{\textrm{Im} A_{\xi_i}\}_{1\leq i\leq n}$ are orthogonal. Thus, any pair of shape operator in
$\{\textrm{Im} A_{\xi_i}\}_{1\leq i\leq n}$ are orthogonal. Thus, any pair of shape operator in  $\{A_{\xi_j}\}_{1\leq j\leq n}$ commutes, and we conclude from the Ricci equation that g has flat normal bundle.
$\{A_{\xi_j}\}_{1\leq j\leq n}$ commutes, and we conclude from the Ricci equation that g has flat normal bundle.
From Equation (36), we have  $0\leq\textrm{rank } A_{\xi_j}\leq 2$,
$0\leq\textrm{rank } A_{\xi_j}\leq 2$, ![]() $1\leq j\leq n$. In fact,
$1\leq j\leq n$. In fact,  $\textrm{rank } A_{\xi_j}=2$,
$\textrm{rank } A_{\xi_j}=2$, ![]() $1\leq j\leq n$, for if
$1\leq j\leq n$, for if ![]() $\textrm{rank } A_{\xi_r}\leq 1$ for some
$\textrm{rank } A_{\xi_r}\leq 1$ for some ![]() $1\leq r\leq n$, then there is
$1\leq r\leq n$, then there is ![]() $0\neq Y\in\textrm{span}\{X_r,JX_r\}\cap\ker A_{\xi_r}$. But then Equation (36) yields
$0\neq Y\in\textrm{span}\{X_r,JX_r\}\cap\ker A_{\xi_r}$. But then Equation (36) yields ![]() $Y\in\mathcal{N}(\alpha^g)$ in contradiction with
$Y\in\mathcal{N}(\alpha^g)$ in contradiction with ![]() $A_g=-I$.
$A_g=-I$.
At any point ![]() $x\in M^{2n}$, there exist orthonormal normal vectors
$x\in M^{2n}$, there exist orthonormal normal vectors ![]() $\{\xi_j(x)\}_{1\leq j\leq n}$ and orthogonal tangent vectors
$\{\xi_j(x)\}_{1\leq j\leq n}$ and orthogonal tangent vectors ![]() $\{X_j(x), JX_j(x)\}_{1\leq j\leq n}$ such that
$\{X_j(x), JX_j(x)\}_{1\leq j\leq n}$ such that  $\ker A_{\xi_j(x)}=\oplus_{i\neq j}E_i(x)$, where we denote
$\ker A_{\xi_j(x)}=\oplus_{i\neq j}E_i(x)$, where we denote ![]() $E_j(x)=\textrm{span}\{X_j(x),JX_j(x)\}$.
$E_j(x)=\textrm{span}\{X_j(x),JX_j(x)\}$.
From Equation (36) and since f has flat normal bundle, then at any ![]() $x\in M^{2n}$, there is
$x\in M^{2n}$, there is ![]() $r=r(x)$,
$r=r(x)$, ![]() $0\leq r\leq n$, such that the tangent space decomposes orthogonally as
$0\leq r\leq n$, such that the tangent space decomposes orthogonally as
where ![]() $F_i(x)\oplus F_{n+i}(x)=E_i(x)$ if
$F_i(x)\oplus F_{n+i}(x)=E_i(x)$ if ![]() $0\leq i\leq r$ and
$0\leq i\leq r$ and ![]() $F_i(x)=E_i(x)$ if
$F_i(x)=E_i(x)$ if ![]() $r+1\leq i\leq n$, such that for each
$r+1\leq i\leq n$, such that for each ![]() $\xi\in N_fM(x)$, there exists pairwise distinct
$\xi\in N_fM(x)$, there exists pairwise distinct ![]() $\lambda_i(\xi)\in\mathbb{R}$,
$\lambda_i(\xi)\in\mathbb{R}$, ![]() $1\leq i\leq n+r$, satisfying
$1\leq i\leq n+r$, satisfying
Since the maps ![]() $\xi\mapsto\lambda_i(\xi)$ are linear, then there are unique pairwise distinct vectors
$\xi\mapsto\lambda_i(\xi)$ are linear, then there are unique pairwise distinct vectors ![]() $\eta_i(x)\in N_fM(x)$,
$\eta_i(x)\in N_fM(x)$, ![]() $1\leq i\leq n+r$, such that
$1\leq i\leq n+r$, such that
and
On each connected component Mr of the open dense subset of ![]() $M^{2n}$, where the function r(x) is constant, the maps
$M^{2n}$, where the function r(x) is constant, the maps ![]() $x\in M_r\mapsto\eta_i(x)$ and
$x\in M_r\mapsto\eta_i(x)$ and ![]() $x\in M_r\mapsto F_i(x)$,
$x\in M_r\mapsto F_i(x)$, ![]() $1\leq i\leq n+r$, define smooth vector fields and smooth vector bundles, respectively.
$1\leq i\leq n+r$, define smooth vector fields and smooth vector bundles, respectively.
If ![]() $F_i(x)\oplus F_{n+i}(x)=E_i(x)$, let
$F_i(x)\oplus F_{n+i}(x)=E_i(x)$, let ![]() $Y\in E_i(x)$ satisfy
$Y\in E_i(x)$ satisfy ![]() $A_{\xi_i}Y=\mu Y\neq 0$ and
$A_{\xi_i}Y=\mu Y\neq 0$ and ![]() $A_{\xi_i}JY=\bar\mu JY\neq 0$. Let
$A_{\xi_i}JY=\bar\mu JY\neq 0$. Let ![]() $(Z)_F$ denote taking the F-component of the vector Z. Then Equation (37) gives
$(Z)_F$ denote taking the F-component of the vector Z. Then Equation (37) gives
 \begin{align*}
\mu Y
&=A_{\xi_i}Y
=A_{\xi_i}(Y)_{F_i}+A_{\xi_i}(Y)_{F_{n+i}}
=\langle\xi_i,\eta_i\rangle(Y)_{F_i}+\langle\xi_i,\eta_{n+i}\rangle(Y)_{F_{n+i}},\\
\bar\mu JY&=A_{\xi_i}JY
=A_{\xi_i}(JY)_{F_i}+A_{\xi_i}(JY)_{F_{n+i}}
=\langle\xi_i,\eta_i\rangle(JY)_{F_i}+\langle\xi_i,\eta_{n+i}\rangle(JY)_{F_{n+i}},\\
0&=A_{\xi_i}X_j=A_{\xi_i}(X_j)_{F_j}+A_{\xi_i}(X_j)_{F_{n+j}}
=\langle\xi_i,\eta_j\rangle(X_j)_{F_j}+\langle\xi_i,\eta_{n+j}\rangle(X_j)_{F_{n+j}},\\
0&=A_{\xi_i}JX_j=A_{\xi_i}(JX_j)_{F_j}+A_{\xi_i}(JX_j)_{F_{n+j}}
=\langle\xi_i,\eta_j\rangle(JX_j)_{F_j}+\langle\xi_i,\eta_{n+j}\rangle(JX_j)_{F_{n+j}},
\end{align*}
\begin{align*}
\mu Y
&=A_{\xi_i}Y
=A_{\xi_i}(Y)_{F_i}+A_{\xi_i}(Y)_{F_{n+i}}
=\langle\xi_i,\eta_i\rangle(Y)_{F_i}+\langle\xi_i,\eta_{n+i}\rangle(Y)_{F_{n+i}},\\
\bar\mu JY&=A_{\xi_i}JY
=A_{\xi_i}(JY)_{F_i}+A_{\xi_i}(JY)_{F_{n+i}}
=\langle\xi_i,\eta_i\rangle(JY)_{F_i}+\langle\xi_i,\eta_{n+i}\rangle(JY)_{F_{n+i}},\\
0&=A_{\xi_i}X_j=A_{\xi_i}(X_j)_{F_j}+A_{\xi_i}(X_j)_{F_{n+j}}
=\langle\xi_i,\eta_j\rangle(X_j)_{F_j}+\langle\xi_i,\eta_{n+j}\rangle(X_j)_{F_{n+j}},\\
0&=A_{\xi_i}JX_j=A_{\xi_i}(JX_j)_{F_j}+A_{\xi_i}(JX_j)_{F_{n+j}}
=\langle\xi_i,\eta_j\rangle(JX_j)_{F_j}+\langle\xi_i,\eta_{n+j}\rangle(JX_j)_{F_{n+j}},
\end{align*}where i ≠ j. Thus, the vectors ηi, ![]() $\eta_{n+i}$ are non-zero and satisfy
$\eta_{n+i}$ are non-zero and satisfy ![]() $\eta_i,\eta_{n+i}\in\textrm{span}\{\xi_i\}$. Hence, the vector fields
$\eta_i,\eta_{n+i}\in\textrm{span}\{\xi_i\}$. Hence, the vector fields ![]() $\eta_1,\ldots,\eta_n$ form an orthogonal frame and
$\eta_1,\ldots,\eta_n$ form an orthogonal frame and ![]() $\xi_i\in\textrm{span}\{\eta_i\}$,
$\xi_i\in\textrm{span}\{\eta_i\}$, ![]() $1\leq i\leq n$. It follows that on Mr, the orthonormal vector fields
$1\leq i\leq n$. It follows that on Mr, the orthonormal vector fields ![]() $\xi_1,\ldots,\xi_n$ are smooth.
$\xi_1,\ldots,\xi_n$ are smooth.
Next we argue on Mr. The Codazzi equation ![]() $(\nabla_SA)(T,\xi_j)=(\nabla_TA)(S,\xi_j)$ gives
$(\nabla_SA)(T,\xi_j)=(\nabla_TA)(S,\xi_j)$ gives
 \begin{equation*}
A_{\xi_j}[S,T]+A_{\nabla_S^\perp\xi_j}T=A_{\nabla_T^\perp\xi_j}S
\end{equation*}
\begin{equation*}
A_{\xi_j}[S,T]+A_{\nabla_S^\perp\xi_j}T=A_{\nabla_T^\perp\xi_j}S
\end{equation*}for any  $S,T\in \ker A_{\xi_j}$. Being the vector subspaces
$S,T\in \ker A_{\xi_j}$. Being the vector subspaces  $\{\textrm{Im} A_{\xi_j}\}_{1\leq j \leq n}$ orthogonal, we have
$\{\textrm{Im} A_{\xi_j}\}_{1\leq j \leq n}$ orthogonal, we have
 \begin{equation*}
\langle\nabla_S^\perp\xi_j,\xi_k\rangle A_{\xi_k}T
=\langle\nabla_T^\perp\xi_j,\xi_k\rangle A_{\xi_k}S,\quad
1\leq j\neq k\leq n
\end{equation*}
\begin{equation*}
\langle\nabla_S^\perp\xi_j,\xi_k\rangle A_{\xi_k}T
=\langle\nabla_T^\perp\xi_j,\xi_k\rangle A_{\xi_k}S,\quad
1\leq j\neq k\leq n
\end{equation*}for any  $S,T\in\ker A_{\xi_j}$. Since
$S,T\in\ker A_{\xi_j}$. Since ![]() $\textrm{rank } A_{\xi_k}=2$, then the ξj’s are parallel in the normal connection along
$\textrm{rank } A_{\xi_k}=2$, then the ξj’s are parallel in the normal connection along  $\ker A_{\xi_j}$, and hence along TMr.
$\ker A_{\xi_j}$, and hence along TMr.
Let ![]() $Y\in E_j$ satisfy
$Y\in E_j$ satisfy  $A_{\xi_j}Y=\lambda Y$. Then the above Codazzi equation also gives
$A_{\xi_j}Y=\lambda Y$. Then the above Codazzi equation also gives
 \begin{equation*}
\lambda\nabla_SY=A_{\xi_j}[S,Y]-S(\lambda)Y\in E_j
\end{equation*}
\begin{equation*}
\lambda\nabla_SY=A_{\xi_j}[S,Y]-S(\lambda)Y\in E_j
\end{equation*}for any  $S\in\ker A_{\xi_j}$,
$S\in\ker A_{\xi_j}$, ![]() $1\leq j\leq n$. Thus, the subbundle Ej is parallel along
$1\leq j\leq n$. Thus, the subbundle Ej is parallel along  $\ker A_{\xi_j}$. Hence, by Equation (36) and since
$\ker A_{\xi_j}$. Hence, by Equation (36) and since  $\textrm{rank } A_{\xi_j}=2$, we have
$\textrm{rank } A_{\xi_j}=2$, we have
 \begin{equation*} \begin{array}{c}
\langle\nabla_{X_j}Y,X_k\rangle=-\langle Y,\nabla_{X_j}X_k\rangle=0,\qquad
\langle\nabla_{JX_j}Y,X_k\rangle=-\langle Y,\nabla_{JX_j}X_k\rangle=0,\\
\langle\nabla_{X_j}Y,JX_k\rangle=-\langle Y,\nabla_{X_j}JX_k\rangle=0, \quad
\langle\nabla_{JX_j}Y,JX_k\rangle=-\langle Y,\nabla_{JX_j}JX_k\rangle=0
\quad\textrm{if}\ j\neq k,
\end{array}
\end{equation*}
\begin{equation*} \begin{array}{c}
\langle\nabla_{X_j}Y,X_k\rangle=-\langle Y,\nabla_{X_j}X_k\rangle=0,\qquad
\langle\nabla_{JX_j}Y,X_k\rangle=-\langle Y,\nabla_{JX_j}X_k\rangle=0,\\
\langle\nabla_{X_j}Y,JX_k\rangle=-\langle Y,\nabla_{X_j}JX_k\rangle=0, \quad
\langle\nabla_{JX_j}Y,JX_k\rangle=-\langle Y,\nabla_{JX_j}JX_k\rangle=0
\quad\textrm{if}\ j\neq k,
\end{array}
\end{equation*}and therefore the Ej’s are parallel along Mr. Then by the de Rham theorem, there is an open subset ![]() $U\subset M_r$, which decomposes in a Riemannian product
$U\subset M_r$, which decomposes in a Riemannian product ![]() $M_1^2\times\cdots\times M_n^2$ of surfaces. Since the codimension of g is n and
$M_1^2\times\cdots\times M_n^2$ of surfaces. Since the codimension of g is n and ![]() $\alpha^g(Y_i,Y_j)=0$, if
$\alpha^g(Y_i,Y_j)=0$, if ![]() $Y_i\in E_i$ and
$Y_i\in E_i$ and ![]() $Y_j\in E_j$, i ≠ j, then by Theorem 8.7 in [Reference Dajczer and Tojeiro4], there are isometric immersions
$Y_j\in E_j$, i ≠ j, then by Theorem 8.7 in [Reference Dajczer and Tojeiro4], there are isometric immersions ![]() $g_1\colon M_1^2\to\mathbb{L}^3$ and
$g_1\colon M_1^2\to\mathbb{L}^3$ and  $g_j\colon M_j^2\to\mathbb{R}^3$,
$g_j\colon M_j^2\to\mathbb{R}^3$, ![]() $2\leq j\leq n$, such that
$2\leq j\leq n$, such that
Since ![]() $g(M)\subset\mathbb{H}^{3n-1}$, then
$g(M)\subset\mathbb{H}^{3n-1}$, then ![]() $\langle g,g\rangle=-1$. Hence,
$\langle g,g\rangle=-1$. Hence, ![]() $\langle g_j{}_*X_j,g_j\rangle=\langle g_*X_j,g\rangle=0$, and therefore,
$\langle g_j{}_*X_j,g_j\rangle=\langle g_*X_j,g\rangle=0$, and therefore, ![]() $\|g_j\|=r_j$ with
$\|g_j\|=r_j$ with  $-r_1^2+\sum_{j=2}^nr_j^2=-1$.
$-r_1^2+\sum_{j=2}^nr_j^2=-1$.
We are now in conditions to give the remaining proofs of the results stated in the introduction.
Proof of Theorem 2
First observe that it suffices to prove that this result holds on some open subset of ![]() $M^{2n}$. By Theorem 3, we have that
$M^{2n}$. By Theorem 3, we have that ![]() $p=n-1$. In an open neighbourhood U of x 0 in
$p=n-1$. In an open neighbourhood U of x 0 in ![]() $M^{2n}$, there is a complex vector subbundle
$M^{2n}$, there is a complex vector subbundle ![]() $\bar{V}\subset TM$ such that
$\bar{V}\subset TM$ such that ![]() $\bar{V}(x_0)=V^{2m}$,
$\bar{V}(x_0)=V^{2m}$, ![]() $m\geq n-1$, and that
$m\geq n-1$, and that ![]() $K(S,JS) \gt 0$ for any
$K(S,JS) \gt 0$ for any ![]() $0\neq S\in\bar{V}$. Suppose that at
$0\neq S\in\bar{V}$. Suppose that at ![]() $y\in U$, there is a J-invariant vector subspace
$y\in U$, there is a J-invariant vector subspace ![]() $V_1\subset T_yU$ such that the subspace
$V_1\subset T_yU$ such that the subspace ![]() ${\cal S}(\beta|_{V_1\times V_1})$ is degenerate and
${\cal S}(\beta|_{V_1\times V_1})$ is degenerate and ![]() $2\bar{s}=\dim{\cal S}(\beta|_{V_1\times V_1})\leq\dim V_1-2$. Then by part (iii) of Proposition 13, there exists a J-invariant vector
$2\bar{s}=\dim{\cal S}(\beta|_{V_1\times V_1})\leq\dim V_1-2$. Then by part (iii) of Proposition 13, there exists a J-invariant vector ![]() $P^{2m}\subset T_yU$ with
$P^{2m}\subset T_yU$ with ![]() $m\geq n-\bar{s}+1$ such that
$m\geq n-\bar{s}+1$ such that ![]() $K(S,JS)\leq 0$ for any
$K(S,JS)\leq 0$ for any ![]() $S\in P^{2m}$. Now by Proposition 9, we have
$S\in P^{2m}$. Now by Proposition 9, we have ![]() $\bar{s}\leq p=n-1$. Hence,
$\bar{s}\leq p=n-1$. Hence, ![]() $m\geq 2$, and this is a contradiction. Thus, the vector subspace
$m\geq 2$, and this is a contradiction. Thus, the vector subspace ![]() ${\cal S}(\beta)$ is non-degenerate. From Proposition 15, we obtain that
${\cal S}(\beta)$ is non-degenerate. From Proposition 15, we obtain that ![]() $s=n=p+1$, that is, that β is surjective. The proof now follows from Proposition 15 and Lemma 18.
$s=n=p+1$, that is, that β is surjective. The proof now follows from Proposition 15 and Lemma 18.
Proof of Theorem 5
Recall that ![]() $\alpha^g(X,Y)=i_*\alpha^f(X,Y)+\langle X,Y\rangle g$. Let U be the subset of points of
$\alpha^g(X,Y)=i_*\alpha^f(X,Y)+\langle X,Y\rangle g$. Let U be the subset of points of ![]() $M^{2n}$ such that at any
$M^{2n}$ such that at any ![]() $x\in U$, there is a J-invariant vector subspace
$x\in U$, there is a J-invariant vector subspace ![]() $V_1\subset T_xM$ such that
$V_1\subset T_xM$ such that  $\bar\beta=\beta|_{V_1\times V_1}$ satisfies that
$\bar\beta=\beta|_{V_1\times V_1}$ satisfies that ![]() ${\cal S}(\bar\beta)$ is a degenerate subspace and
${\cal S}(\bar\beta)$ is a degenerate subspace and ![]() $\dim{\cal S}(\bar\beta)\leq\dim V_1-2$. If the subspace
$\dim{\cal S}(\bar\beta)\leq\dim V_1-2$. If the subspace ![]() ${\cal S}(\beta(x))$ is degenerate for
${\cal S}(\beta(x))$ is degenerate for ![]() $x\in M^{2n}$, then
$x\in M^{2n}$, then ![]() $x\in U$. In fact, we have for s in Equation (6) that
$x\in U$. In fact, we have for s in Equation (6) that ![]() $s \lt p+1$ since, otherwise,
$s \lt p+1$ since, otherwise, ![]() ${\cal S}(\beta(x))=N_gM(x)\oplus N_gM(x)$, and therefore this subspace would be non-degenerate. Having that
${\cal S}(\beta(x))=N_gM(x)\oplus N_gM(x)$, and therefore this subspace would be non-degenerate. Having that ![]() $p=n-1$, then
$p=n-1$, then ![]() $\dim{\cal S}(\beta)=2s\leq 2p=2n-2=\dim T_xM-2$, and thus
$\dim{\cal S}(\beta)=2s\leq 2p=2n-2=\dim T_xM-2$, and thus ![]() $x\in U$.
$x\in U$.
Under the above conditions, Proposition 13 applies to ![]() $\bar\beta(x)$ for
$\bar\beta(x)$ for ![]() $x\in U$. Then by part (ii), there are a unit space-like vector
$x\in U$. Then by part (ii), there are a unit space-like vector ![]() $i_*\eta(x)\perp g(x)$ defined by
$i_*\eta(x)\perp g(x)$ defined by ![]() $v=i_*\eta(x)+g(x)$ and the Lorentzian plane
$v=i_*\eta(x)+g(x)$ and the Lorentzian plane ![]() $L=\textrm{span}\,\{i_*\eta(x),g(x)\}$ such that for
$L=\textrm{span}\,\{i_*\eta(x),g(x)\}$ such that for ![]() $P\subset N_fM(x)$ given by
$P\subset N_fM(x)$ given by ![]() $i_*P=L^\perp$, we have
$i_*P=L^\perp$, we have
 \begin{equation}
\alpha^f(X,Y)(x)=\alpha^f_P(X,Y)(x)+\langle X,Y\rangle\eta(x),
\end{equation}
\begin{equation}
\alpha^f(X,Y)(x)=\alpha^f_P(X,Y)(x)+\langle X,Y\rangle\eta(x),
\end{equation}where  $i_*\alpha^f_P(X,Y)=\alpha^g_{L^\perp}(X,Y)$. From Equation (15) applied to
$i_*\alpha^f_P(X,Y)=\alpha^g_{L^\perp}(X,Y)$. From Equation (15) applied to ![]() $\bar\beta$, we obtain that
$\bar\beta$, we obtain that  $\bar\beta_1=\pi_{L^\perp\times L^\perp}\circ \bar\beta$ satisfies
$\bar\beta_1=\pi_{L^\perp\times L^\perp}\circ \bar\beta$ satisfies ![]() $\dim\mathcal{N}(\bar\beta_1(x))\geq 4$. If
$\dim\mathcal{N}(\bar\beta_1(x))\geq 4$. If ![]() $S\in\mathcal{N}(\bar\beta_1(x))$, then Equation (14) gives
$S\in\mathcal{N}(\bar\beta_1(x))$, then Equation (14) gives
 \begin{equation*}
0=\bar\beta_1(S,S)=(\alpha_{L^\perp}^g(S,S)+\alpha_{L^\perp}^g(JS,JS),0).
\end{equation*}
\begin{equation*}
0=\bar\beta_1(S,S)=(\alpha_{L^\perp}^g(S,S)+\alpha_{L^\perp}^g(JS,JS),0).
\end{equation*} It now follows from Equation (38) that for any ![]() $x\in U$, we have
$x\in U$, we have
 \begin{equation}
\alpha^f(S,S)=\alpha^f_P(S,S)+\|S\|^2\eta(x)
\quad\textrm{and}\quad
\alpha^f(JS,JS)=-\alpha^f_P(S,S)+\|S\|^2\eta(x).
\end{equation}
\begin{equation}
\alpha^f(S,S)=\alpha^f_P(S,S)+\|S\|^2\eta(x)
\quad\textrm{and}\quad
\alpha^f(JS,JS)=-\alpha^f_P(S,S)+\|S\|^2\eta(x).
\end{equation} Suppose that there exists an open subset ![]() $U_0\subset M^{2n}$ such that
$U_0\subset M^{2n}$ such that ![]() $U\cap U_0=\emptyset$. We have by Proposition 15, Lemma 18 and Theorem 2 that
$U\cap U_0=\emptyset$. We have by Proposition 15, Lemma 18 and Theorem 2 that ![]() $g=i\circ f\colon M^{2n}\to\mathbb{L}^{3n}$ is as given by the latter result. Then g(M) is unbounded due to completeness of
$g=i\circ f\colon M^{2n}\to\mathbb{L}^{3n}$ is as given by the latter result. Then g(M) is unbounded due to completeness of ![]() $M^{2n}$ and the presence of the hyperbolic factor, and hence also f(M) is unbounded.
$M^{2n}$ and the presence of the hyperbolic factor, and hence also f(M) is unbounded.
By the above, it remains to consider the case when U is dense in ![]() $M^{2n}$. We denote by
$M^{2n}$. We denote by ![]() $r\colon\mathbb{H}^{3n-1}\to[0,+\infty)$ the distance function in
$r\colon\mathbb{H}^{3n-1}\to[0,+\infty)$ the distance function in ![]() $\mathbb{H}^{3n-1}$ to a reference point and set
$\mathbb{H}^{3n-1}$ to a reference point and set ![]() $h=\cosh(r\circ f)$. Then Equation (14) in [Reference Dajczer and Vlachos5] states that
$h=\cosh(r\circ f)$. Then Equation (14) in [Reference Dajczer and Vlachos5] states that
for any ![]() $X\in T_xM$. On the other hand, we have from Equation (39) that
$X\in T_xM$. On the other hand, we have from Equation (39) that
 \begin{equation*}
\langle\textrm{grad}\, r(f(x)),\alpha^f(S,S)\rangle=\langle\textrm{grad}\, r(f(x)),\alpha^f_P(S,S)\rangle
+\langle\textrm{grad}\, r(f(x)),\eta(x)\rangle\|S\|^2
\end{equation*}
\begin{equation*}
\langle\textrm{grad}\, r(f(x)),\alpha^f(S,S)\rangle=\langle\textrm{grad}\, r(f(x)),\alpha^f_P(S,S)\rangle
+\langle\textrm{grad}\, r(f(x)),\eta(x)\rangle\|S\|^2
\end{equation*}and
 \begin{equation*}
\langle\textrm{grad}\, r(f(x)),\alpha^f(JS,JS)\rangle=-\langle\textrm{grad}\, r(f(x)),\alpha^f_P(S,S)\rangle
+\langle\textrm{grad}\, r(f(x)),\eta(x)\rangle\|S\|^2
\end{equation*}
\begin{equation*}
\langle\textrm{grad}\, r(f(x)),\alpha^f(JS,JS)\rangle=-\langle\textrm{grad}\, r(f(x)),\alpha^f_P(S,S)\rangle
+\langle\textrm{grad}\, r(f(x)),\eta(x)\rangle\|S\|^2
\end{equation*}for any ![]() $x\in U$ and
$x\in U$ and ![]() $S\in\mathcal{N}(\bar\beta_1(x))$. Then Equation (40) yields
$S\in\mathcal{N}(\bar\beta_1(x))$. Then Equation (40) yields
 \begin{align}
\textrm{Hess}\, h(x)(S,S)&+\textrm{Hess}\, h(x)(JS,JS)\\
&=2\,\cosh (r(f(x)))
+2\,\sinh (r(f(x)))\langle\textrm{grad}\, r(f(x)),\eta(x)\rangle\|S\|^2\nonumber
\end{align}
\begin{align}
\textrm{Hess}\, h(x)(S,S)&+\textrm{Hess}\, h(x)(JS,JS)\\
&=2\,\cosh (r(f(x)))
+2\,\sinh (r(f(x)))\langle\textrm{grad}\, r(f(x)),\eta(x)\rangle\|S\|^2\nonumber
\end{align}for any ![]() $x\in U$ and
$x\in U$ and ![]() $S\in\mathcal{N}(\bar\beta_1(x))$.
$S\in\mathcal{N}(\bar\beta_1(x))$.
If f(M) is bounded, by the Omori-Yau maximal principle for the Hessian, there exists a sequence ![]() $\{x_k\}_{k\in\mathbb{N}}$ in
$\{x_k\}_{k\in\mathbb{N}}$ in ![]() $M^{2n}$ such that
$M^{2n}$ such that
 \begin{equation*}
\lim h(x_k)=\sup\{h\} \lt +\infty\quad\textrm{and}\quad
\textrm{Hess}\, h(x_k)(X_k,X_k)\leq \frac{1}{k}\|X_k\|^2\quad \textrm{for any}\
X_k\in T_{x_k}M.
\end{equation*}
\begin{equation*}
\lim h(x_k)=\sup\{h\} \lt +\infty\quad\textrm{and}\quad
\textrm{Hess}\, h(x_k)(X_k,X_k)\leq \frac{1}{k}\|X_k\|^2\quad \textrm{for any}\
X_k\in T_{x_k}M.
\end{equation*} Let ![]() $U_k\subset M^{2n}$ be an open neighbourhood containing xk such that
$U_k\subset M^{2n}$ be an open neighbourhood containing xk such that
 \begin{equation*}
|h(x_k)-h(y)| \lt \frac{1}{k}
\quad\textrm{and}\quad
\textrm{Hess}\, h(y)(X,X)\leq \frac{2}{k}\|X\|^2
\end{equation*}
\begin{equation*}
|h(x_k)-h(y)| \lt \frac{1}{k}
\quad\textrm{and}\quad
\textrm{Hess}\, h(y)(X,X)\leq \frac{2}{k}\|X\|^2
\end{equation*}for any ![]() $y\in U_k$ and
$y\in U_k$ and ![]() $X\in T_yM$. By the above, we have that
$X\in T_yM$. By the above, we have that ![]() $U\cap U_k\neq\emptyset$ for any
$U\cap U_k\neq\emptyset$ for any ![]() $k\in\mathbb{N}$. Then there exists a sequence
$k\in\mathbb{N}$. Then there exists a sequence ![]() $y_k\in U_k\cap U$ such that
$y_k\in U_k\cap U$ such that ![]() $r^*=\lim r(f(y_k)) \gt 0$ when
$r^*=\lim r(f(y_k)) \gt 0$ when ![]() $k\mapsto+\infty$. We obtain from Equation (41) that
$k\mapsto+\infty$. We obtain from Equation (41) that
 \begin{equation*}
\frac{2}{k}\geq \cosh r(f(y_k)))
+\sinh r(f(y_k)))\langle\textrm{grad}\, r(f(y_k)),\eta(y_k)\rangle
\end{equation*}
\begin{equation*}
\frac{2}{k}\geq \cosh r(f(y_k)))
+\sinh r(f(y_k)))\langle\textrm{grad}\, r(f(y_k)),\eta(y_k)\rangle
\end{equation*} Taking the limit as ![]() $k\mapsto+\infty$ and using that
$k\mapsto+\infty$ and using that ![]() $\|\textrm{grad}\, r\|=1$ gives
$\|\textrm{grad}\, r\|=1$ gives
and this is a contradiction.
Proof of Theorem 6
Proposition 15 applies on an open subset ![]() $U\subset M^{2n}$ where
$U\subset M^{2n}$ where ![]() ${\cal S}(\beta)$ is non-degenerate. We obtain that n = 3 and that g(U) is as described by Lemma 18. Then the result follows from Theorem 2. Therefore, we may assume that
${\cal S}(\beta)$ is non-degenerate. We obtain that n = 3 and that g(U) is as described by Lemma 18. Then the result follows from Theorem 2. Therefore, we may assume that ![]() ${\cal S}(\beta)$ is degenerate at any point of
${\cal S}(\beta)$ is degenerate at any point of ![]() $M^{2n}$. By Equation (7), the subspaces
$M^{2n}$. By Equation (7), the subspaces ![]() ${\cal S}(\beta)\cap({\cal S}(\beta))^\perp$ have dimension two and form a smooth vector subbundle. Hence, there is a smooth normal vector field
${\cal S}(\beta)\cap({\cal S}(\beta))^\perp$ have dimension two and form a smooth vector subbundle. Hence, there is a smooth normal vector field ![]() $v\in\Gamma(N_gM)$ such that
$v\in\Gamma(N_gM)$ such that ![]() $\langle v,g\rangle=-1$ and Equation (21) holds. Let
$\langle v,g\rangle=-1$ and Equation (21) holds. Let ![]() $\eta\in\Gamma(N_fM)$ be the smooth unit vector field such that
$\eta\in\Gamma(N_fM)$ be the smooth unit vector field such that ![]() $v=i_*\eta+g$. Then Equation (21) gives
$v=i_*\eta+g$. Then Equation (21) gives  $A_\eta^f=I$. The Codazzi equation yields that η is parallel in the normal connection along the open dense subset of non-flat points of
$A_\eta^f=I$. The Codazzi equation yields that η is parallel in the normal connection along the open dense subset of non-flat points of ![]() $M^{2n}$ and then on all of
$M^{2n}$ and then on all of ![]() $M^{2n}$. Hence, f(M) is contained in a horosphere.
$M^{2n}$. Hence, f(M) is contained in a horosphere.
Funding Statement
Marcos Dajczer is supported by the grant PID2021-124157NB-I00 funded by MCIN/AEI/10.13039/501100011033/ ‘ERDF A way of making Europe’, Spain, and is also supported by Comunidad Autónoma de la Región de Murcia, Spain, within the framework of the Regional Programme in Promotion of the Scientific and Technical Research (Action Plan 2022), by Fundación Séneca, Regional Agency for Science and Technology, REF, 21899/PI/22. Marcos Dajczer was partially supported by both grants.