Let q be a power of a prime p, let 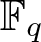$\mathbb F_q$ be the finite field with q elements and, for each nonconstant polynomial 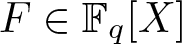$F\in \mathbb F_{q}[X]$ and each integer 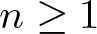$n\ge 1$, let 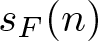$s_F(n)$ be the degree of the splitting field (over 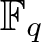$\mathbb F_q$) of the iterated polynomial 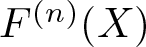$F^{(n)}(X)$. In 1999, Odoni proved that 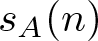$s_A(n)$ grows linearly with respect to n if 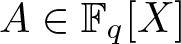$A\in \mathbb F_q[X]$ is an additive polynomial not of the form 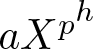$aX^{p^h}$; moreover, if q = p and 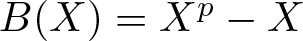$B(X)=X^p-X$, he obtained the formula 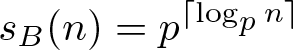$s_{B}(n)=p^{\lceil \log_p n\rceil}$. In this paper we note that 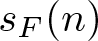$s_F(n)$ grows at least linearly unless 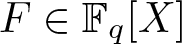$F\in \mathbb F_q[X]$ has an exceptional form and we obtain a stronger form of Odoni’s result, extending it to affine polynomials. In particular, we prove that if A is additive, then 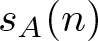$s_A(n)$ resembles the step function 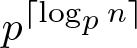$p^{\lceil \log_p n\rceil}$ and we indeed have the identity 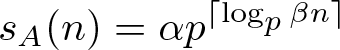$s_A(n)=\alpha p^{\lceil \log_p \beta n\rceil}$ for some 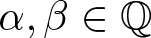$\alpha, \beta\in \mathbb Q$, unless A presents a special irregularity of dynamical flavour. As applications of our main result, we obtain statistics for periodic points of linear maps over 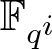$\mathbb F_{q^i}$ as 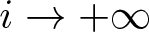$i\to +\infty$ and for the factorization of iterates of affine polynomials over finite fields.