Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-07T06:31:50.528Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse multiparameter eigenvalue problems for matrices III

Published online by Cambridge University Press:  20 January 2009

Patrick J. Browne  and
B. D. Sleeman
Patrick J. Browne
Affiliation:
Department of Mathematics and StatisticsUniversity of CalgaryCalgaryAlbertaCanadaT2N 1N4
B. D. Sleeman
Affiliation:
Department of Mathematical SciencesUniversity of DundeeDundee DD1 4HNScotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This note will complement and, in a certain sense, complete our earlier studies [3, 4] of the theory of inverse multiparameter eigenvalue problems for matrices. In those papers, we considered the so called “additive inverse problem” which, briefly stated for the 2-parameter case, asks for conditions on given n × n matrices A, B, C and on given points (si, ti) ∈ ℝ2, 1 ≦ i ≦ n, under which a diagonal matrix D can be found so that the 2-parameter eigenvalue problem

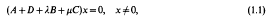
can be solved when (λ,μ)=(si, ti), 1 = i = n. Put another way, we look for conditions ensuring that the points (si, ti), 1 ≦ i ≦ n, belong to the eigenvalues of (1.1).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 31 , Issue 1 , February 1988 , pp. 151 - 155
Copyright
Copyright © Edinburgh Mathematical Society 1988

References

REFERENCES

1.Binding, P. and Browne, P. J., Spectral properties of two-parameter eigenvalue problems, Proc. Roy. Soc. Edinburgh 89A (1981), 157–173.CrossRefGoogle Scholar
2.Blum, E. K., Numerical Analysis and Computation, Theory and Practice (Addison-Wesley, Reading, Mass. 1972).Google Scholar
3.Browne, P. J. and Sleeman, B. D., Inverse multiparameter eigenvalue problems for matrices, Proc. Roy. Soc. Edinburgh 100A (1985), 29–38.CrossRefGoogle Scholar
4.Browne, P. J. and Sleeman, B. D., Inverse multiparameter eigenvalue problems for matrices, II, Proc. Edinburgh Math. Soc. 29 (1986), 343–348.CrossRefGoogle Scholar
5.Hadeler, K. P., Ein inverses eigenwert problem, Linear Algebra Appl. 1 (1968), 83–101.CrossRefGoogle Scholar
6.Hadeler, K. P., Multiplicative inverse eigenvert probleme, Linear Algebra Appl. 1 (1969), 65–86.CrossRefGoogle Scholar
7.Hadeler, K. P., Existenz- und eindeutigkeitssätze für engenwertaufgaben mil hilfe des topologischen abbildungsgrades, Arch. Rat. Mech. Anal. 42 (1971), 317–322.CrossRefGoogle Scholar
8.Lloyd, N. G., Degree Theory (Cambridge University Press, 1978).Google Scholar