Following the papers by H. W. Turnbull and J. Williamson, I have verified that the 122 forms, of the system of two quaternary quadrics 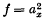and are actually irreducible. The original 1917 system contained 125 forms, which Williamson reduced by three. The present verification shews that no further reduction is possible. The proof was carried out as follows. I first constructed the whole system in canonical form with 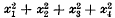and 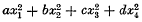for the two quadrics, and then listed the degrees in the coefficients and variables u, p, x of these concomitants. I next made Diophantine equations between these degrees for testing the supposed reducibility and found them to be impossible, except for Williamson's reduced forms.