In a previous paper [Spain, Proc. Roy. Soc. Edinburgh, Vol. LX (1940), 134], I have shown that the application of the cardinal function to the problem of interpolating the derivatives yields the result

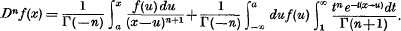
This formula is valid for x > a (the constant of integration), and R(n) < 0. The analytical continuation for R(n) ≥ 0. is indicated in the paper just quoted. The first term is the familiar expression for a fractional derivative, but the second term is not Riemann's complementary function. Furthermore, this result is unsatisfactory because it is impossible to perform the repeated operation of a fractional derivative of a fractional derivative.