No CrossRef data available.
Published online by Cambridge University Press: 11 January 2024
Li, Ma and Wang have provided in [13] a partial classification of the so-called Moebius deformable hypersurfaces, that is, the umbilic-free Euclidean hypersurfaces 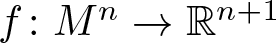 $f\colon M^n\to \mathbb{R}^{n+1}$ that admit non-trivial deformations preserving the Moebius metric. For
$f\colon M^n\to \mathbb{R}^{n+1}$ that admit non-trivial deformations preserving the Moebius metric. For 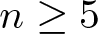 $n\geq 5$, the classification was completed by the authors in [12]. In this article we obtain an infinitesimal version of that classification. Namely, we introduce the notion of an infinitesimal Moebius variation of an umbilic-free immersion
$n\geq 5$, the classification was completed by the authors in [12]. In this article we obtain an infinitesimal version of that classification. Namely, we introduce the notion of an infinitesimal Moebius variation of an umbilic-free immersion 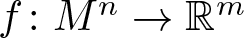 $f\colon M^n\to \mathbb{R}^m$ into Euclidean space as a one-parameter family of immersions
$f\colon M^n\to \mathbb{R}^m$ into Euclidean space as a one-parameter family of immersions 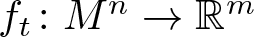 $f_t\colon M^n\to \mathbb{R}^m$, with
$f_t\colon M^n\to \mathbb{R}^m$, with 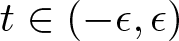 $t\in (-\epsilon, \epsilon)$ and
$t\in (-\epsilon, \epsilon)$ and 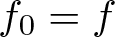 $f_0=f$, such that the Moebius metrics determined by ft coincide up to the first order. Then we characterize isometric immersions
$f_0=f$, such that the Moebius metrics determined by ft coincide up to the first order. Then we characterize isometric immersions 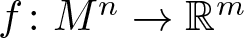 $f\colon M^n\to \mathbb{R}^m$ of arbitrary codimension that admit a non-trivial infinitesimal Moebius variation among those that admit a non-trivial conformal infinitesimal variation, and use such characterization to classify the umbilic-free Euclidean hypersurfaces of dimension
$f\colon M^n\to \mathbb{R}^m$ of arbitrary codimension that admit a non-trivial infinitesimal Moebius variation among those that admit a non-trivial conformal infinitesimal variation, and use such characterization to classify the umbilic-free Euclidean hypersurfaces of dimension  $n\geq 5$ that admit non-trivial infinitesimal Moebius variations.
$n\geq 5$ that admit non-trivial infinitesimal Moebius variations.