Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:57:37.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Indicial equivalents of multiparameter definiteness conditions in finite dimensions

Published online by Cambridge University Press:  20 January 2009

Paul Binding
Paul Binding
Affiliation:
Department of Mathematics and StatisticsUniversity of Calgary
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Tm, Vmn be Hermitean linear operators on complex Hilbert spaces Hm, m=1…k. A nonzero column vector 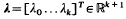satisfying

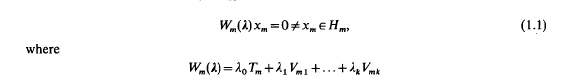
will be called an eigenvalue. This type of problem has been studied extensively by Atkinson [2] from the viewpoint of determinantal operators on the tensor product 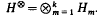We shall connect his work with more recent investigations [5,7] of eigenvalue indices based on minimax principles for 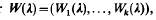, which can be viewed as an operator on .

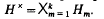Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 3 , October 1984 , pp. 283 - 296
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

REFERENCES

1.Atkinson, F. V., Discrete and Continuous Boundary Problems (Academic Press, 1964).Google Scholar
2.Atkinson, F. V.Multiparameter Eigenvalue Problems vol. 1 (Academic Press, 1972).Google Scholar
3.Binding, P. A.Multiparameter definiteness conditions, Proc. Roy. Soc. Edin. 89A (1981), 319–332.Google Scholar
4.Binding, P. A.Multiparameter definiteness conditions II, Proc. Roy. Soc. Edin. 93A (1982), 47–61.Google Scholar
5.Binding, P. A.Abstract oscillation theorems for multiparameter eigenvalue problems, J. Diff. Equations 49 (1983), 331–343.Google Scholar
6.Binding, P. A. and Browne, P. J.A variational approach to multiparameter eigenvalue problems in Hilbert space, SIAM J. Math. Anal. 9 (1978), 1054–1067.Google Scholar
7.Binding, P. A., Browne, P. J. and Turyn, L.Existence conditions for two parameter eigenvalue problems, Proc. Roy. Soc. Edin. 91A (1981), 15–30.CrossRefGoogle Scholar
8.Sleeman, B. D.Multiparameter Eigenvalue Problems in Hilbert Space (Pitman, 1978).Google Scholar