Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shkarin, Stanislav
2011.
On supercyclicity of operators from a supercyclic semigroup.
Journal of Mathematical Analysis and Applications,
Vol. 382,
Issue. 2,
p.
516.
Frerick, Leonhard
Jordá, Enrique
Kalmes, Thomas
and
Wengenroth, Jochen
2014.
Strongly continuous semigroups on some Fréchet spaces.
Journal of Mathematical Analysis and Applications,
Vol. 412,
Issue. 1,
p.
121.


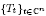 with holomorphic dependence on the parameter
with holomorphic dependence on the parameter 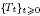 .
.