Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T02:31:23.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Homotopy of the exceptional Lie group G2

Published online by Cambridge University Press:  20 January 2009

Shichiro Oka
Shichiro Oka
Affiliation:
Department of Mathematics, Kyushu University, Fukuoka A12, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be one of the following compact simply connected Lie groups: SU(3), Sp(2), G2. In the first two cases there is a well known stable decomposition of G as Q ∨ Sd where d = dim G and Q is a certain subspace of G. For SU(3), Q is the stunted complex quasiprojective space Σ(ℂP2/ℂP1) which fits into a cofibration sequence S3→Q→S5 with stable attaching map η:S5 → S4 For Sp(2), Q is the quaternionic quasi-projective space ℍℚ1 and fits into a cofibration sequence S3→Q→S7 with stable attaching map 2ν:S7→S4 (Here η and ν are generators of 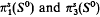respectively.)

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 2 , June 1986 , pp. 145 - 169
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

REFERENCES

1.Adams, J. F., Vector fields on spheres, Ann. of Math. 75 (1962), 603–632.CrossRefGoogle Scholar
2.Adams, J. F., On the group J(X}-IV, Topology 5 (1966), 21–71.CrossRefGoogle Scholar
3.Atiyah, M. F., Vector bundles and the Künneth formula, Topology 1 (1962), 245–248.CrossRefGoogle Scholar
4.Atiyah, M. F., On the K-theory of compact Lie groups, Topology 4 (1965), 65–99.CrossRefGoogle Scholar
5.Borel, A., Sur l'homologie et la cohomologie des groupes de Lie compacts connexes, Amer. J. Math. 76 (1954), 273–324.CrossRefGoogle Scholar
6.Bott, R. and Samelson, H., Applications of the theory of Morse to symmetric spaces, Amer. J. Math. 80 (1958), 964–1029.CrossRefGoogle Scholar
7.Browder, W. and Spanier, E. H., H-spaces and duality, Pacific J. Math. 12 (1962), 411–414.CrossRefGoogle Scholar
8.Cohen, F. R. and Peterson, F. P., Suspensions of Stiefel manifolds, Quart. J. Math. Oxford 35 (1984), 115–119.CrossRefGoogle Scholar
9.Hodgkin, L., On the K-theory of Lie groups, Topology 6 (1967), 1–36.CrossRefGoogle Scholar
10.Maruyama, K., Note on self H-maps of SU(3), Mem. Fac. Sci. Kyushu Univ. Ser. A 38 (1984), 5–8.Google Scholar
11.Maruyama, K. and Oka, S., Self-H-maps of H-spaces of type (3,7),Mem. Fac. Sci. Kyushu Univ. Ser. A 35 (1981), 375–383.Google Scholar
12.Mimura, M., The homotopy groups of Lie groups of low rank, J. Math. Kyoto Univ. 6 (1967), 131–176.Google Scholar
13.Mimura, M., Nishida, G. and Toda, H., On the classification of H-spaces of rank 2, J. Math. Kyoto Univ. 13 (1973), 611–627.Google Scholar
14.Mimur, M. and Sawashita, N., On the group of self-homotopy equivalences of H-spaces of rank 2, J. Math. Kyoto Univ. 21 (1981), 331–349.Google Scholar
15.Mimura, M. and Toda, H., Homotopy groups of SU(3), SU(4) and Sp(2), J. Math. Kyoto Univ. 3 (1964), 217–250.Google Scholar
16.Mukai, J., Stable homotopy of some elementary complexes, Mem. Fac. Sci. Kyushu Univ. Ser. A 20 (1966), 266–282.Google Scholar
17.Oka, S., On the group of self-homotopy equivalences of H-spaces of low rank, II, Mem. Fac. Sci. Kyushu Univ. Ser. A 35 (1981), 307–323.Google Scholar
18.Oka, S., Small ring spectra and p-rank of the stable homotopy of spheres, Proceedings of the Northwestern Homotopy Theory Conference (Contemporary Mathematics 19, American Math. Soc, Providence, RI, 1983), 267–308.CrossRefGoogle Scholar
19.Oka, S., Multiplicative structure of finite ring spectra and stable homotopy of spheres, Proceedings of the Aarhus Algebraic Topology Conference 1982 (ed. Madsen and Oliver, Springer Lecture Notes in Mathematics, No. 1051), 418–441.Google Scholar
20.Sawashita, N., Self H-equivalences of H-spaces with applications to H-spaces of rank 2, Hiroshima Math. J. 14 (1984), 75–113.CrossRefGoogle Scholar
21.Toda, H., Composition methods in homotopy groups of spheres (Annals of Math. Studies 49, Princeton UP, Princeton, NJ, 1962).Google Scholar
22.Toda, H., On spectra realizing exterior parts of the Steenrod algebra, Topology 10 (1971), 53–66.CrossRefGoogle Scholar
23.Yokota, I., Groups and representations (in Japanese), Shôkabô, Tokyo, 1973).Google Scholar