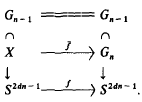Hostname: page-component-f554764f5-44mx8 Total loading time: 0 Render date: 2025-04-09T04:36:40.948Z Has data issue: false hasContentIssue false
  • English
  • Français

Homotopy associativity of sphere extensions

Published online by Cambridge University Press:  20 January 2009

N. Iwase
N. Iwase
Affiliation:
Permanent Address: Department of MathematicsOkayama UniversityTsushima-Naka Okayama 700, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Throughout this paper, we work in the category of (p-localized) spaces having the homotopy type of connected CW-complexes of finite type with base point. We consider a principal bundle

where Gn = SU(n), U(n) or Sp(n) and d = 1, 1 or 2 respectively. In this case, the bundle is obtained as an induced bundle by a mapping f of base space S2dn−1 from the classical group extension as follows:

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , Issue 3 , October 1989 , pp. 459 - 472
Copyright
Copyright © Edinburgh Mathematical Society 1989

References

REFERENCES

1.Adams, J. F., On Chern characters and the structure of the unitary group, Proc. Cambridge Philos. Soc. 57 (1961), 189–199.CrossRefGoogle Scholar
2.Adams, J. F., On the groups J(X). II, Topology 3 (1965), 137–172.CrossRefGoogle Scholar
3.Adams, J. F., Lectures on generalized cohomology, Lecture 4, Category Theory, Homology Theory and their Applications III (Lecture Notes in Math. 99, Springer, Berlin 1969), 77–113.CrossRefGoogle Scholar
4.Curtis, M. and Mislin, G., Two new H-spaces, Bull. Amer. Math. Soc. 4 (1970), 851–852.CrossRefGoogle Scholar
5.Goncalves, D. L., Mod 2 Homotopy-associative H-spaces, Geometric Application of Homotopy Theory I (Lecture Notes in Math. 657 Springer, Berlin, 1978), 198–216.CrossRefGoogle Scholar
6.Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers (Oxford University Press, London, 1954).Google Scholar
7.Hemmi, Y., Homotopy associative H-spaces and sphere extensions of classical groups, preprint.Google Scholar
8.Hilton, P. and Roitberg, J. R., On principal S 3-bundles over spheres, Ann. of Math. 90 (1969), 91–107.CrossRefGoogle Scholar
9.Hubbuck, J. R., Generalized cohomology operations and H-spaces of low rank, Trans. Amer. Math. Soc. 141 (1969), 335–360.Google Scholar
10.Hubbuck, J. R., Primitivity in torsion free cohomology Hopf algebras, Comment. Math. Helv. 46 (1971), 13–43.CrossRefGoogle Scholar
11.Hubbuck, J. R., Some Pontrjagin rings, I, Proc. Roy. Soc. Edinburgh Sect. A 90 (1981), 237–256.CrossRefGoogle Scholar
12.Hubbuck, J. R. and Mimura, M., Certain p-regular H-spaces, Arch. Math. 49 (1987), 79–82.CrossRefGoogle Scholar
13.Iwase, N., On the K-ring structure of X-projective n-space, Mem. Fac. Sci. Kyushu Univ. Ser. A 38 (1984), 285–297.Google Scholar
14.Iwase, N. and Mimura, M., Higher homotopy associativity, to appear in Arcata Proceedings.Google Scholar
15.Sigrist, F. and Suter, U., Sur l'associativité homotopie des H-espaces de rang 2, C. R. Acad. Sci. Paris 238 (1971), 890–892.Google Scholar
16.Sigrist, F. and Suter, U., Eine Anwendung der K-theorie in der H-Räume, Comment. Math. Helv. 47 (1972), 36–52.CrossRefGoogle Scholar
17.Stasheff, J. D., Homotopy associativity of H-spaces I and II, Trans. Amer. Math. Soc. 108 (1963), 275–292 and 293–312.Google Scholar
18.Stasheff, J. D., Manifolds of the homotopy type of (non Lie) groups, Bull. Amer. Math. Soc. 75 (1969), 998–1000.CrossRefGoogle Scholar
19.Zabrodsky, A., On sphere extensions of classical Lie groups, Transactions of the Summer Conference on Algebraic Topology (Madison, Wisconsin, 1970).Google Scholar
20.Zabrodsky, A., On spherical classes in the cohomology of H-spaces, H-spaces Neuchâtel (Suisse) Aout 1970 (Lecture Notes in Math. 196 Springer, Berlin, 1971), 25–33.CrossRefGoogle Scholar
21.Zabrodsky, A., The classification of simply connected H-spaces with three cells I, Math. Scand. 30 (1972), 193–210.CrossRefGoogle Scholar
22.Zabrodsky, A., On the construction of new finite CW-W-spaces, Invent. Math. 16 (1972), 260–266.CrossRefGoogle Scholar