Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T03:21:44.509Z Has data issue: false hasContentIssue false
  • English
  • Français

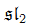Higher-Level Conformal Blocks Divisors on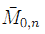

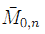Published online by Cambridge University Press:  16 January 2014

Valery Alexeev ,
Angela Gibney  and
David Swinarski
Valery Alexeev
Affiliation:
Department of Mathematics, The University of Georgia, Athens, GA 30602, USA ([email protected]; [email protected])
Angela Gibney
Affiliation:
Department of Mathematics, The University of Georgia, Athens, GA 30602, USA ([email protected]; [email protected])
David Swinarski
Affiliation:
Department of Mathematics, Lincoln Center Campus, Fordham University, New York, NY 10023, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a family of semi-ample divisors on the moduli space of n-pointed genus 0 curves given by higher-level 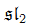conformal blocks. We derive formulae for their intersections with a basis of 1-cycles, show that they form a basis for the Sn-invariant Picard group, and generate a full-dimensional subcone of the Sn-invariant nef cone. We find their position in the nef cone and study their associated morphisms.

Keywords

moduli spacevector bundlesconformal field theoryPrimary 14D2114E30Secondary 14D2281T40
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 57 , Issue 1 , February 2014 , pp. 7 - 30
Copyright
Copyright © Edinburgh Mathematical Society 2014 

References

1.Arakelov, S. Ju., Families of algebraic curves with fixed degeneracies, Izv. Akad. Nauk SSSR Ser. Mat. 35 (1971), 1269–1293.Google Scholar
2.Arap, M., Gibney, A., Stankewicz, J. and Swinarski, D., level conformai blocks divisors on , Int. Math. Res. Not. 2012(7) (2012), 1634–1680.Google Scholar
3.Beauville, A., Conformal blocks, fusion rules and the Verlinde formula, in Proc. Hirzebruch 65 Conf. on Algebraic Geometry, May 2-7, 1993, Israel Mathematical Conference Proceedings, Volume 9, pp. 75–96 (Bar-Ilan University, Ramat Gan, 1996).Google Scholar
4.Birkar, C., Cascini, P., Hacon, C. D. and McKernan, J., Existence of minimal models for varieties of log general type, J. Am. Math. Soc. 23 (2010), 405–468.Google Scholar
5.Cornalba, M. and Harris, J., Divisor classes associated to families of stable varieties, with applications to the moduli space of curves, Annales Scient. Éc. Norm. Sup. 21(3) (1988), 455–475.CrossRefGoogle Scholar
6.Dolgachev, I. V. and Hu, Y., Variation of geometric invariant theory quotients, Publ. Math. IHES 87(1) (1998), 5–56.Google Scholar
7.Faber, C., Chow rings of moduli spaces of curves, I, The Chow ring of , Annals Math. 132(2) (1990), 331–419.CrossRefGoogle Scholar
8.Fakhruddin, N., Chern classes of conformal blocks, in Compact moduli spaces and vector bundles, Contemporary Mathematics, Volume 564, pp. 145–176 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
9.Farkas, G. and Gibney, A., The Mori cones of moduli spaces of pointed curves of small genus, Trans. Am. Math. Soc. 355(3) (2003), 1183–1199.Google Scholar
10.Fedorchuk, M., Cyclic covering morphisms on , eprint (arXiv:1105.0655, 2011).Google Scholar
11.Feingold, A. J., Fusion rules for affine Kac–Moody algebras, in Kac–Moody Lie Algebras and Related Topics: Proc. Ramanujan Int. Symp. on Kac–Moody Lie Algebras and Applications, January 28–31, 2002, Contemporary Mathematics, Volume 343, pp. 53–96 (American Mathematical Society, Providence, RI, 2004).Google Scholar
12.Gawrilow, E. and Joswig, M., POLYMAKE: a framework for analyzing convex polytopes, Version 2.3, in Polytopes: combinatorics and computation, Deutsche Mathematiker-Vereinigung Seminar, Volume 29, pp. 43–73 (Birkhäuser, 2000) (available at www.math.tu-berlin.de/polymake).CrossRefGoogle Scholar
13.Giansiracusa, N., Conformal blocks and rational normal curves, J. Alg. Geom. 22 (2013), 773–793.Google Scholar
14.Giansiracusa, N. and Gibney, A., The cone of type A, level 1, conformal blocks divisors, Adv. Math. 231(2) (2012), 798–814.Google Scholar
15.Giansiracusa, N. and Simpson, M., GIT compactifications of M0,n from conics, Int. Math. Res. Not. 2011 (14) (2011), 3315–3334.Google Scholar
16.Gibney, A., Numerical criteria for divisors on to be ample, Compositio Math. 145(5) (2009), 1227–1248.Google Scholar
17.Gibney, A., On extensions of the Torelli map, in Geometry and arithmetic, European Mathematical Society Series of Congress Reports, pp. 125–136 (European Mathematical Society, Zurich, 2012).CrossRefGoogle Scholar
18.Gibney, A. and Krashen, D., NEFWIZ: software for divisors on the moduli space of curves, Version 1.1 (2006).Google Scholar
19.Gibney, A., Keel, S. and Morrison, I., Towards the ample cone of , J. Am. Math. Soc. 15(2) (2002), 273–294.Google Scholar
20.Grayson, D. and Stillman, M., Macaulay2: a software system for research in algebraic geometry, Version 1.1 (2008) (available at www.math.uiuc.edu/Macaulay2).Google Scholar
21.Hassett, B., Moduli spaces of weighted pointed stable curves, Adv. Math. 173(2) (2003), 316–352.CrossRefGoogle Scholar
22.Hassett, B., Classical and minimal models of the moduli space of curves of genus two, in Geometric methods in algebra and number theory, Progress in Mathematics, Volume 235, pp. 169–192 (Birkhäuser, 2005).CrossRefGoogle Scholar
23.Hassett, B. and Hyeon, D., Log canonical models for the moduli space of curves: the first divisorial contraction, Trans. Am. Math. Soc. 361(8) (2009), 4471–4489.CrossRefGoogle Scholar
24.Hyeon, D. and Lee, Y., Stability of bicanonical curves of genus three, J. Pure Appl. Alg. 213(10) (2009), 1991–2000.Google Scholar
25.Keel, S., Basepoint freeness for nef and big line bundles in positive characteristic, Annals Math. 149(1) (1999), 253–286.Google Scholar
26.Keel, S. and Mckernan, J., Contractible extremal rays on , in Handbook of moduli, Volume II (ed. Farkas, G. and Morrison, I.), Advanced Lectures in Mathematics, Volume 25 (International Press, Somerville, MA, 2013).Google Scholar
27.Looijenga, E., Conformal blocks revisited, eprint (arXiv:math/0507086v1, 2005).Google Scholar
28.Pandharipande, R., The canonical class of (ℙr, d) and enumerative geometry, Int. Math. Res. Not. 1997(4) (1997), 173–186.Google Scholar
29.Rulla, W., The birational geometry of and , PhD thesis, University of Texas (2001).Google Scholar
30.Schubert, D., A new compactification of the moduli space of curves, Compositio Math. 78(3) (1991), 297–313.Google Scholar
31.Swinarski, D., Conformal Blocks: software for computing conformal block divisors in Macaulay2, Version 1.1 (2011) (available at www.math.uga.edu/~davids/conformalblocks).Google Scholar
32.Thaddeus, M., Geometric invariant theory and flips, J. Am. Math. Soc. 9(3) (1996), 691–723.CrossRefGoogle Scholar
33.Ueno, K., Conformal field theory with gauge symmetry, Fields Institute Monographs, Volume 24 (American Mathematical Society, Providence, RI, 2008).Google Scholar