Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-22T13:48:38.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Hardy spaces and Riesz transforms on a Lie group of exponential growth

Part of: Abstract harmonic analysis Harmonic analysis in several variables Lie groups

Published online by Cambridge University Press:  17 February 2025

Peter Sjögren Open the ORCID record for Peter Sjögren [Opens in a new window]  and
Maria Vallarino Open the ORCID record for Maria Vallarino [Opens in a new window]
Peter Sjögren
Affiliation:
Mathematical Sciences, University of Gothenburg and Mathematical Sciences, Chalmers, Göteborg, Sweden
Maria Vallarino*
Affiliation:
Dipartimento di Scienze Matematiche “Giuseppe Luigi Lagrange” - Politecnico di Torino, Corso Duca degli Abruzzi, Torino, Italy
*
Corresponding author: Maria Vallarino, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be the Lie group 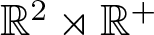${\mathbb{R}}^2\rtimes {\mathbb{R}}^+$ endowed with the Riemannian symmetric space structure. Take a distinguished basis 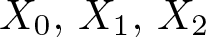$X_0,\, X_1,\,X_2$ of left-invariant vector fields of the Lie algebra of G, and consider the Laplacian $\Delta=-\sum_{i=0}^2X_i^2$ and the first-order Riesz transforms 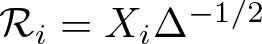$\mathcal R_i=X_i\Delta^{-1/2}$, 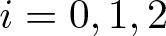$i=0,1,2$. We first show that the atomic Hardy space H1 in G introduced by the authors in a previous paper does not admit a characterization in terms of the Riesz transforms 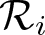$\mathcal R_i$. It is also proved that two of these Riesz transforms are bounded from H1 to H1.

Keywords

Riesz transformsHardy spaceLie groupsexponential growth

MSC classification

Primary: 42B30: $H^p$-spaces
Secondary: 22E30: Analysis on real and complex Lie groups 43A80: Analysis on other specific Lie groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 32
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Martini, A., F., Santagati and Vallarino., M Heat kernel and Riesz transform for the flow Laplacian on homogeneous trees, (New Trends in) Complex and Fourier Analysis, N., Arcozzi, M. M., Peloso, A., Tabacco, (Springer INdAM Series, Springer),(to appear).Google Scholar
Auscher, P., McIntosh, A. and Russ, E., Hardy spaces of differential forms and Riesz transforms on Riemannian manifolds, C. R. Math. Acad. Sci. Paris 344(2): (2007), 103–108.CrossRefGoogle Scholar
Carbonaro, A., Mauceri, G. and Meda, S., H 1 and BMO for certain locally doubling metric measure spaces, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 8(3): (2009), 543–582.Google Scholar
Carbonaro, A., McIntosh, A. and Morris, A. J., Local Hardy spaces of differential forms on Riemannian manifolds, J. Geom. Anal. 23(1): (2013), 106–169.CrossRefGoogle Scholar
Celotto, D. and Meda, S., On the analogue of the Fefferman-Stein theorem on graphs with the Cheeger property, Ann. Mat. Pura Appl. (4) 197(5): (2018), 1637–1677.CrossRefGoogle Scholar
Coifman, R. R. and Weiss, G., Analyse harmonique non commutative sur certains espaces homogenes. Lecture Notes in Mathematics 242 (Berlin-New York: Springer, 1971).Google Scholar
Coifman, R. R. and Weiss, G., Extensions of Hardy spaces and their use in analysis, Bull. Am. Math. Soc. 83(4) (1977), 569–645.CrossRefGoogle Scholar
Cowling, M., Giulini, S., Hulanicki, A. and Mauceri, G., phSpectral multipliers for a distinguished Laplacian on certain groups of exponential growth, Studia Math. 111(2): (1994), 103–121.CrossRefGoogle Scholar
Dziubański, J., Riesz transforms characterizations of Hardy spaces H 1 for the rational Dunkl setting and multidimensional Bessel operators, J. Geom. Anal. 26(4): (2016), 2639–2663.CrossRefGoogle Scholar
Dziubański, J. and Preisner, M., Riesz transform characterization of Hardy spaces associated with Schrödinger operators with compactly supported potentials, Ark. Mat. 48(2): (2010), 301–310.CrossRefGoogle Scholar
Betancor, J., Dziubański, J. and Garrigós, G., Riesz transform characterization of Hardy spaces associated with certain Laguerre expansions, Tohoku Math. J. 62(1): (2010), 215–231.CrossRefGoogle Scholar
Giulini, S. and Sjögren, P., A note on maximal functions on a solvable Lie group, Arch. Math. 55(2): (1990), 156–160.CrossRefGoogle Scholar
Hebisch, W. and Steger, T., Multipliers and singular integrals on exponential growth groups, Math. Z. 245(1): (2003), 37–61.CrossRefGoogle Scholar
Levi, M., Martini, A., Santagati, F., Tabacco, A. and Vallarino, M., Riesz transform for a flow Laplacian on homogeneous trees, J. Fourier Anal. Appl. 29(2): (2023), .CrossRefGoogle Scholar
Lohoué, N. and Varopoulos, N., Remarques sur les transformèes de Riesz sur les groupes de Lie nilpotents, C. R. Acad. Sci. Paris Sér. I Math. 301(11): (1985), 559–560.Google Scholar
Marias, M. and Russ, E., H 1-boundedness of Riesz transforms and imaginary powers of the Laplacian on Riemannian manifolds, Ark. Mat. 41(1): (2003), 115–132.CrossRefGoogle Scholar
Martini, A., Meda, S. and Vallarino, M., A family of Hardy type spaces on nondoubling manifolds, Ann. Mat. Pura Appl. 199(5): (2020), 2061–2085.CrossRefGoogle Scholar
Martini, A., Meda, S., Vallarino, M. and Veronelli, G., Inclusions and noninclusions of Hardy type spaces on certain nondoubling manifolds, J. Funct. Anal. 286(3): (2024), .CrossRefGoogle Scholar
Martini, A., Santagati, F., Tabacco, A. and Vallarino, M., Riesz transform and spectral multipliers for the flow Laplacian on nonhomogeneous trees, arXiv:2310.09113.Google Scholar
Mauceri, G., Meda, S. and Sjögren, P., Endpoint estimates for first-order Riesz transforms associated to the Ornstein-Uhlenbeck operator, Rev. Mat. Iberoam. 28(1): (2012), 77–91.CrossRefGoogle Scholar
Mauceri, G., Meda, S. and Vallarino, M., Higher order Riesz transforms on noncompact symmetric spaces, J. Lie Theory 28(2): (2018), 479–497.Google Scholar
Meda, S. and Veronelli, G., Local Riesz transform and local Hardy spaces on Riemannian manifolds with bounded geometry, J. Geom. Anal. 32(2): (2022), .CrossRefGoogle Scholar
Russ, E., $H^1-L^1$ boundedness of Riesz transforms on Riemannian manifolds and on graphs, Potential Anal. 14(3): (2001), 301–330.CrossRefGoogle Scholar
Saloff-Coste, L., Analyse sur les groupes de Lie à croissance polynomiale, Ark. Mat. 28 2 (1990), 315–331.CrossRefGoogle Scholar
Santagati, F., Hardy spaces on homogeneous trees with flow measures, J. Math. Anal. Appl. 510(2): (2022), .CrossRefGoogle Scholar
Sjögren, P. and Vallarino, M., Boundedness from H 1 to L 1 of Riesz transforms on a Lie group of exponential growth, Ann. Inst. Fourier 58(4): (2008), 1117–1151.CrossRefGoogle Scholar
Sjögren, P. and Vallarino, M., Heat maximal function on a Lie group of exponential growth, Ann. Acad. Sci. Fenn. Math. 37(2): (2012), 491–507.CrossRefGoogle Scholar
Stein, E. M., Harmonic Analysis (Princeton, NJ: Princeton University Press, 1993).Google Scholar
Vallarino, A. M. M., Riesz transforms on solvable extensions of stratified groups, Studia Math. 259(2): (2021), 175–200.Google Scholar
Vallarino, M., Spaces H 1 and BMO on exponential growth groups, Collect. Math. 60(3): (2009), 277–295.CrossRefGoogle Scholar
Vallarino, M., Atomic and maximal Hardy spaces on a Lie group of exponential growth, Trends in harmonic analysis, Springer INdAM Ser., Volume 3 (Springer, Milan, 2013) 409–424.Google Scholar