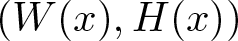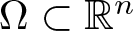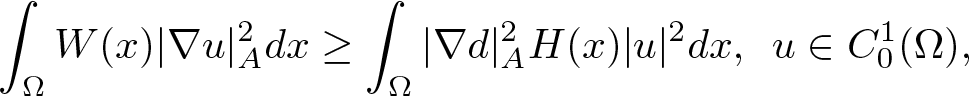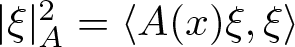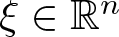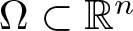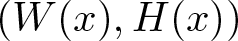1. Introduction
In the work [Reference Ghoussoub and Moradifam17], Ghoussoub and Moradifam gave necessary and sufficient conditions for a Bessel pair of positive radial functions W(x) and H(x) on a ball B of radius R in ![]() $\mathbb{R}^n$, so that one has the Hardy inequality for all functions
$\mathbb{R}^n$, so that one has the Hardy inequality for all functions ![]() $u \in C^{\infty}_0(B)$:
$u \in C^{\infty}_0(B)$:
 \begin{equation*}
\int_{B} W(x) |\nabla u|^2 dx \geq \int_{B} H(x) |u|^2 dx,
\end{equation*}
\begin{equation*}
\int_{B} W(x) |\nabla u|^2 dx \geq \int_{B} H(x) |u|^2 dx,
\end{equation*} and the Hardy–Rellich inequality for all functions ![]() $u \in C^{\infty}_0(B)$:
$u \in C^{\infty}_0(B)$:
 \begin{equation*}
\int_{B} W(x)|\Delta u|^2 dx \geq \int_{B} H(x)|\nabla u|^2 dx +(n-1)\int_{B} \left( \frac{W(x)}{|x|^2}-\frac{W_r(|x|)}{|x|} \right)|\nabla u|^2 dx.
\end{equation*}
\begin{equation*}
\int_{B} W(x)|\Delta u|^2 dx \geq \int_{B} H(x)|\nabla u|^2 dx +(n-1)\int_{B} \left( \frac{W(x)}{|x|^2}-\frac{W_r(|x|)}{|x|} \right)|\nabla u|^2 dx.
\end{equation*} The characterisation of pairs of functions W(x) and H(x) made a very interesting connection between Hardy type inequalities and the oscillatory behaviour of ordinary differential equations. Choosing suitable Bessel pairs ![]() $(W(x),H(x))$ allows one to improve, extend, and unify many results about Hardy and Hardy–Rellich inequalities that were established by Caffarelli et al. [Reference Caffarelli, Kohn and Nirenberg11], Brezis and Vazquez [Reference Brezis and Vazquez10], Wang and Willem [Reference Wang and Willem35], Adimurthi et al. [Reference Adimurthi, Chaudhuri and Ramaswamy1], and other authors. In the book [Reference Ghoussoub and Moradifam16], Ghoussoub and Moradifam posed two questions:
$(W(x),H(x))$ allows one to improve, extend, and unify many results about Hardy and Hardy–Rellich inequalities that were established by Caffarelli et al. [Reference Caffarelli, Kohn and Nirenberg11], Brezis and Vazquez [Reference Brezis and Vazquez10], Wang and Willem [Reference Wang and Willem35], Adimurthi et al. [Reference Adimurthi, Chaudhuri and Ramaswamy1], and other authors. In the book [Reference Ghoussoub and Moradifam16], Ghoussoub and Moradifam posed two questions:
• Develop suitable characterisations for a pair of functions
 $(W(x),H(x))$ in order to have the following inequality:
$(W(x),H(x))$ in order to have the following inequality:
 \begin{equation*}
\int_{\Omega} W(x) |\nabla u|_A^2 dx \geq \int_{\Omega} H(x)|u|^2 dx, \,\,\, u \in C^{1}_0(\Omega),
\end{equation*}
\begin{equation*}
\int_{\Omega} W(x) |\nabla u|_A^2 dx \geq \int_{\Omega} H(x)|u|^2 dx, \,\,\, u \in C^{1}_0(\Omega),
\end{equation*}where
 $|\xi|^2_A = \langle A(x)\xi, \xi \rangle$ for
$|\xi|^2_A = \langle A(x)\xi, \xi \rangle$ for  $\xi \in \mathbb{R}^n$ and A(x) is an n × n symmetric, uniformly positive definite matrix defined on a bounded domain
$\xi \in \mathbb{R}^n$ and A(x) is an n × n symmetric, uniformly positive definite matrix defined on a bounded domain  $\Omega \subset \mathbb{R}^n$.
$\Omega \subset \mathbb{R}^n$.• Determine a necessary and sufficient condition for a Bessel pair
 $(W(x),H(x))$ in order to the Rellich inequality to hold:
$(W(x),H(x))$ in order to the Rellich inequality to hold:
 \begin{equation*}
\int_{\Omega} W(x) |\Delta u|^2 dx \geq \int_{\Omega} H(x)|u|^2 dx, \,\,\, u \in C^{\infty}_0(\Omega).
\end{equation*}
\begin{equation*}
\int_{\Omega} W(x) |\Delta u|^2 dx \geq \int_{\Omega} H(x)|u|^2 dx, \,\,\, u \in C^{\infty}_0(\Omega).
\end{equation*}
The aim of this paper is to give suitable characterisations for a Bessel pair of positive radial functions W(x) and H(x) for Hardy and Rellich inequalities on a bounded, connected domain ![]() $\Omega \subset \mathbb{R}^n$ that answers the open problems of Ghoussoub-Moradifam [Reference Ghoussoub and Moradifam16]. We prove Hardy and Rellich inequalities expressing conditions for Bessel pairs in terms of ordinary differential equations associated with the positive weight functions W(x) and H(x). Our approach relies on the first and second order Picone identities. This suggested approach seems very effective, allowing us to recover almost all well-known Hardy and Rellich type inequalities. It is also an extension of the method of Allegretto-Huang [Reference Allegretto and Huang3, Theorem 2.1], by adding the positive weight function W(x). A similar approach was used by the authors [Reference Ruzhansky, Sabitbek and Suragan26] to establish Hardy and Rellich type inequalities for general (real-valued) vector fields with boundary terms. Recently, in [Reference Cazacu12], Cazacu called this method (but without the function W(x)) as the Method of Super-solutions in Hardy and Rellich inequalities that was adopted from Davies [Reference Davies14].
$\Omega \subset \mathbb{R}^n$ that answers the open problems of Ghoussoub-Moradifam [Reference Ghoussoub and Moradifam16]. We prove Hardy and Rellich inequalities expressing conditions for Bessel pairs in terms of ordinary differential equations associated with the positive weight functions W(x) and H(x). Our approach relies on the first and second order Picone identities. This suggested approach seems very effective, allowing us to recover almost all well-known Hardy and Rellich type inequalities. It is also an extension of the method of Allegretto-Huang [Reference Allegretto and Huang3, Theorem 2.1], by adding the positive weight function W(x). A similar approach was used by the authors [Reference Ruzhansky, Sabitbek and Suragan26] to establish Hardy and Rellich type inequalities for general (real-valued) vector fields with boundary terms. Recently, in [Reference Cazacu12], Cazacu called this method (but without the function W(x)) as the Method of Super-solutions in Hardy and Rellich inequalities that was adopted from Davies [Reference Davies14].
This characterisation of Bessel pairs builds an interesting bridge between Hardy (Rellich) type inequalities and ordinary differential equations. In particular, we can extend and improve many results for Hardy and Rellich type inequalities. Let us briefly recall several types of Hardy inequalities that can be recovered:
I. The classical Hardy inequality for
 $n\geq 3$ on a bounded domain
$n\geq 3$ on a bounded domain  $\Omega \subset \mathbb{R}^n$ asserts that
$\Omega \subset \mathbb{R}^n$ asserts that
 \begin{equation*}
\int_{\Omega} |\nabla u|^2 dx \geq \left(\frac{n-2}{2}\right)^2 \int_{\Omega} \frac{|u|^2}{|x|^2} dx,\,\,\, u \in C^1_0(\Omega),
\end{equation*}
\begin{equation*}
\int_{\Omega} |\nabla u|^2 dx \geq \left(\frac{n-2}{2}\right)^2 \int_{\Omega} \frac{|u|^2}{|x|^2} dx,\,\,\, u \in C^1_0(\Omega),
\end{equation*}where the constant is optimal and not attained. This version of Hardy inequality was investigated by many authors see [Reference Davies14, Reference Goldstein, Kombe and Yener18, Reference Kufner and Opic20, Reference Ruzhansky and Suragan27] and the references therein.
II. The geometric Hardy inequality for any bounded convex domain
 $\Omega \subset \mathbb{R}^n$ with smooth boundary asserts that
$\Omega \subset \mathbb{R}^n$ with smooth boundary asserts that
 \begin{equation*}
\int_{\Omega} |\nabla u|^2 dx \geq \frac{1}{4} \int_{\Omega} \frac{|u|^2}{\delta^2(x)} dx,\,\,\, u \in C^1_0(\Omega),
\end{equation*}
\begin{equation*}
\int_{\Omega} |\nabla u|^2 dx \geq \frac{1}{4} \int_{\Omega} \frac{|u|^2}{\delta^2(x)} dx,\,\,\, u \in C^1_0(\Omega),
\end{equation*}where
 $\delta(x):= dist(x,\partial \Omega)$ is the Euclidean distance to boundary
$\delta(x):= dist(x,\partial \Omega)$ is the Euclidean distance to boundary  $\partial \Omega$ and the constant is also optimal and not attained. There is a number of studies related to this subject, see e.g. [Reference Ancona4–Reference Avkhadiev and Wirths6, Reference Davies14, Reference Kufner and Opic20, Reference Maz’ya22, Reference Ruzhansky, Sabitbek and Suragan31].
$\partial \Omega$ and the constant is also optimal and not attained. There is a number of studies related to this subject, see e.g. [Reference Ancona4–Reference Avkhadiev and Wirths6, Reference Davies14, Reference Kufner and Opic20, Reference Maz’ya22, Reference Ruzhansky, Sabitbek and Suragan31].III. The multipolar Hardy inequality on a bounded domain
 $\Omega \subset \mathbb{R}^n$ asserts that:
$\Omega \subset \mathbb{R}^n$ asserts that:
 \begin{equation*}
\int_{\Omega} |\nabla u|^2 dx \geq C \sum_{i=1}^k\int_{\Omega} \frac{|u|^2}{|x-a_i|^2} dx,\,\,\, u \in C^1_0(\Omega),
\end{equation*}
\begin{equation*}
\int_{\Omega} |\nabla u|^2 dx \geq C \sum_{i=1}^k\int_{\Omega} \frac{|u|^2}{|x-a_i|^2} dx,\,\,\, u \in C^1_0(\Omega),
\end{equation*}where k is the number of poles. This type of inequalities was studied by Felli-Terracini [Reference Felli and Terracini15], Bosi-Dolbeault-Esteban [Reference Bosi, Dolbeault and Esteban9] and Cacazu-Zuazua [Reference Cazacu and Zuazua13].
In this study, we have established the following significant results:
1. Hardy inequality with Bessel pairs: For ![]() $1 \lt p \lt Q$, we demonstrate that the Hardy inequality:
$1 \lt p \lt Q$, we demonstrate that the Hardy inequality:
 \begin{equation*}
\int_{\Omega} W(x) |\nabla u|^p_A dx \geq \int_{\Omega}|\nabla d|^p_A H(x) |u|^p dx,
\end{equation*}
\begin{equation*}
\int_{\Omega} W(x) |\nabla u|^p_A dx \geq \int_{\Omega}|\nabla d|^p_A H(x) |u|^p dx,
\end{equation*} holds true for all complex-valued functions ![]() $u \in C^1_0(\Omega)$, provided that the positive functions W(x) and H(x) satisfy the following conditions:
$u \in C^1_0(\Omega)$, provided that the positive functions W(x) and H(x) satisfy the following conditions:
 \begin{equation*}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation*}
\begin{equation*}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation*} \begin{equation}
\int_{r_0}^{\infty} \left( \frac{\phi(s)}{s^{Q-1}W(s)}\right)^{\frac{1}{p-1}} ds \leq \frac{1}{2(p-1)} \,\,\, \text{for some} \,\,\, r_0 \gt 0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \left( \frac{\phi(s)}{s^{Q-1}W(s)}\right)^{\frac{1}{p-1}} ds \leq \frac{1}{2(p-1)} \,\,\, \text{for some} \,\,\, r_0 \gt 0,
\end{equation}where d(x) is a quasi-norm (see Theorem 2.1).
2. Rellich inequality with Bessel pairs: For ![]() $1 \lt p \lt n$, we have established that the Rellich inequality:
$1 \lt p \lt n$, we have established that the Rellich inequality:
 \begin{equation*}
\int_{\Omega} W(x) |\Delta |u||^p dx \geq \int_{\Omega} H(x) |u|^p dx,
\end{equation*}
\begin{equation*}
\int_{\Omega} W(x) |\Delta |u||^p dx \geq \int_{\Omega} H(x) |u|^p dx,
\end{equation*} is proven to hold for all complex-valued functions ![]() $u \in C^2_0(\Omega)$. The necessary condition for this is the existence of a positive function
$u \in C^2_0(\Omega)$. The necessary condition for this is the existence of a positive function ![]() $v\in C^{2}(\Omega)$ satisfying:
$v\in C^{2}(\Omega)$ satisfying:
with the positive functions W(x) and H(x) being such that ![]() $-\Delta v \gt 0$ almost everywhere in Ω (see Theorem 3.1).
$-\Delta v \gt 0$ almost everywhere in Ω (see Theorem 3.1).
This paper is organised as follows: Section 2 begins by presenting present our main result regarding the weighted Hardy inequality, as detailed in Theorem 2.1. We discuss the preliminaries, focusing on the existence of non-negative solutions to the quasilinear second-order differential equation. This discussion is crucial as it lays the foundation for understanding the characterisation of Bessel pairs W(x) and H(x). Also, we provide examples in various settings, including the Euclidean Space, Heisenberg group, Engel group, and Cartan group. In ![]() $\S$ 3, we prove the weighted Rellich inequality by establishing the necessary and sufficient conditions for the Bessel pair W(x) and H(x). Moreover, some particular cases are discussed.
$\S$ 3, we prove the weighted Rellich inequality by establishing the necessary and sufficient conditions for the Bessel pair W(x) and H(x). Moreover, some particular cases are discussed.
2. Hardy inequalities with Bessel pairs
Let ![]() $\Omega \subset \mathbb{R}^n$ be a bounded domain with smooth boundary. Define
$\Omega \subset \mathbb{R}^n$ be a bounded domain with smooth boundary. Define
 \begin{equation}
\mathcal{L}_{p,A} f = - \sum_{i,j=1}^n \frac{\partial}{\partial {x_j}} \left( a_{ij}(x)|\nabla f|^{p-2}_A \frac{\partial f}{\partial x_j} \right),
\end{equation}
\begin{equation}
\mathcal{L}_{p,A} f = - \sum_{i,j=1}^n \frac{\partial}{\partial {x_j}} \left( a_{ij}(x)|\nabla f|^{p-2}_A \frac{\partial f}{\partial x_j} \right),
\end{equation}and
 \begin{equation*}
|\nabla f|^2_A = \sum_{i,j=1}^n a_{ij}(x) \frac{\partial f}{\partial x_i} \frac{\partial f}{\partial x_j},
\end{equation*}
\begin{equation*}
|\nabla f|^2_A = \sum_{i,j=1}^n a_{ij}(x) \frac{\partial f}{\partial x_i} \frac{\partial f}{\partial x_j},
\end{equation*} where ![]() $A(x)=(a_{ij}(x))$ is an n × n symmetric, uniformly positive definite matrix with smooth coefficients defined on Ω.
$A(x)=(a_{ij}(x))$ is an n × n symmetric, uniformly positive definite matrix with smooth coefficients defined on Ω.
Let ![]() $\Phi_p$ be a constant multiple of the fundamental solution (e.g. [Reference Boccardo and Galloutet7, Reference Kilpelainen and Maly21]) for
$\Phi_p$ be a constant multiple of the fundamental solution (e.g. [Reference Boccardo and Galloutet7, Reference Kilpelainen and Maly21]) for ![]() $\mathcal{L}_{p,A}$ that solves the equation:
$\mathcal{L}_{p,A}$ that solves the equation:
From ![]() $\Phi_p$, we are able to define the quasi-norm:
$\Phi_p$, we are able to define the quasi-norm:
 \begin{equation}
d(x) := \left\{\begin{matrix}
\Phi_p(x)^{\frac{p-1}{p-Q}}, & \text{for} \,\,\, x \neq 0,\\
0,& \text{for} \,\,\, x = 0,
\end{matrix}\right.
\end{equation}
\begin{equation}
d(x) := \left\{\begin{matrix}
\Phi_p(x)^{\frac{p-1}{p-Q}}, & \text{for} \,\,\, x \neq 0,\\
0,& \text{for} \,\,\, x = 0,
\end{matrix}\right.
\end{equation} where Q is the appropriate homogeneous dimension and ![]() $1 \lt p \lt Q$.
$1 \lt p \lt Q$.
Define
 \begin{equation}
\Psi_{\mathcal{L}_A}(x) := |\nabla d|^2_A(x),
\end{equation}
\begin{equation}
\Psi_{\mathcal{L}_A}(x) := |\nabla d|^2_A(x),
\end{equation} for x ≠ 0. The function ![]() $\Psi_{\mathcal{L}_A}(x)$ can be calculated for the explicit form of the quasi-norm d(x). For example:
$\Psi_{\mathcal{L}_A}(x)$ can be calculated for the explicit form of the quasi-norm d(x). For example:
• In the Euclidean setting, when
 $\mathcal{L}_A= \Delta$ is the standard Laplace operator, then
$\mathcal{L}_A= \Delta$ is the standard Laplace operator, then  $\Psi_{\Delta}(x) =1$.
$\Psi_{\Delta}(x) =1$.• In the Heisenberg group, when
 $\mathcal{L}_A= \mathcal{L}_{\mathbb{H}}$ is the sub-Laplacian and the quasi-norm (
$\mathcal{L}_A= \mathcal{L}_{\mathbb{H}}$ is the sub-Laplacian and the quasi-norm ( $\mathcal{L}$-gauge)
$\mathcal{L}$-gauge)  $d_{\mathbb{H}}(x)$, then
$d_{\mathbb{H}}(x)$, then  $\Psi_{\mathcal{L}_{\mathbb{H}}}(x) = |x'|^2d_{\mathbb{H}}^{-2}$.
$\Psi_{\mathcal{L}_{\mathbb{H}}}(x) = |x'|^2d_{\mathbb{H}}^{-2}$.• For Baouendi–Grushin operator, when
 $\mathcal{L}_A= \mathcal{L}_{\gamma}$ is the Baouendi–Grushin operator and
$\mathcal{L}_A= \mathcal{L}_{\gamma}$ is the Baouendi–Grushin operator and  $d_{\gamma}(x)$ is associated the quasi-norm, then
$d_{\gamma}(x)$ is associated the quasi-norm, then  $\Psi_{\mathcal{L}_{\gamma}}(x) =|\xi|^{2\gamma}d_{\gamma}^{-2\gamma}$ where
$\Psi_{\mathcal{L}_{\gamma}}(x) =|\xi|^{2\gamma}d_{\gamma}^{-2\gamma}$ where  $x = (\xi,\zeta) \in \mathbb{R}^k\times \mathbb{R}^l$ and γ > 0.
$x = (\xi,\zeta) \in \mathbb{R}^k\times \mathbb{R}^l$ and γ > 0.
In the stratified Lie groups, we shall remark that the function ![]() $\Psi_{\mathcal{L}_A}(x)$ is δλ-homogeneous degree of zero and translation invariant (i.e.
$\Psi_{\mathcal{L}_A}(x)$ is δλ-homogeneous degree of zero and translation invariant (i.e. ![]() $\Psi_{\mathcal{L}}(\alpha \circ x, \alpha \circ y)= \Psi_{\mathcal{L}}(x,y)$ for
$\Psi_{\mathcal{L}}(\alpha \circ x, \alpha \circ y)= \Psi_{\mathcal{L}}(x,y)$ for ![]() $x,y \in \mathbb{G}$ with x ≠ y). Furthermore, the function
$x,y \in \mathbb{G}$ with x ≠ y). Furthermore, the function ![]() $\Psi_{\mathcal{L}_A}(x)$ is the kernel of mean volume formulas (see more [Reference Bonfiglioli, Lanconelli and Uguzzoni8, Definition 5.5.1]).
$\Psi_{\mathcal{L}_A}(x)$ is the kernel of mean volume formulas (see more [Reference Bonfiglioli, Lanconelli and Uguzzoni8, Definition 5.5.1]).
The following theorem characterises the relation between W(x) and H(x) in order to obtain the weighted Hardy inequality:
Theorem 2.1. Let Ω be a bounded domain in ![]() $\mathbb{R}^n$. Let W(x) and H(x) be positive radially symmetric functions. Let
$\mathbb{R}^n$. Let W(x) and H(x) be positive radially symmetric functions. Let ![]() $1 \lt p \lt Q$. Let d(x) be as in (2.2). Then, the inequality
$1 \lt p \lt Q$. Let d(x) be as in (2.2). Then, the inequality
 \begin{equation}
\int_{\Omega} W(x) |\nabla u|^p_A dx \geq \int_{\Omega}|\nabla d|^p_A H(x) |u|^p dx,
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\nabla u|^p_A dx \geq \int_{\Omega}|\nabla d|^p_A H(x) |u|^p dx,
\end{equation} holds for all complex-valued functions ![]() $u \in C^1_0(\Omega)$ provided that the following conditions hold:
$u \in C^1_0(\Omega)$ provided that the following conditions hold:
 \begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation} \begin{equation}
\int_{r_0}^{\infty} \left( \frac{\phi(s)}{s^{Q-1}W(s)}\right)^{\frac{1}{p-1}} ds \leq \frac{1}{2(p-1)} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \left( \frac{\phi(s)}{s^{Q-1}W(s)}\right)^{\frac{1}{p-1}} ds \leq \frac{1}{2(p-1)} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}Remark 2.2. Note that
• As usual, we denote
 $W(x)=W(|x|)$ and
$W(x)=W(|x|)$ and  $H(x)=H(|x|)$. We fix the notation for a positive function
$H(x)=H(|x|)$. We fix the notation for a positive function  $f(x) \gt 0$ and a non-negative function
$f(x) \gt 0$ and a non-negative function  $f(x)\geq 0$.
$f(x)\geq 0$.• For p = 2, Theorem 2.1 answers to the question posed by Ghoussoub-Moradifam [Reference Ghoussoub and Moradifam16].
• For
 $A(x)\equiv 1$, Theorem 2.1 was established for general (real-valued) vector fields with boundary terms by the authors [Reference Ruzhansky, Sabitbek and Suragan26] (see also [Reference Ruzhansky and Suragan27–Reference Ruzhansky and Suragan29, Reference Sabitbek and Suragan33, Reference Sabitbek34]).
$A(x)\equiv 1$, Theorem 2.1 was established for general (real-valued) vector fields with boundary terms by the authors [Reference Ruzhansky, Sabitbek and Suragan26] (see also [Reference Ruzhansky and Suragan27–Reference Ruzhansky and Suragan29, Reference Sabitbek and Suragan33, Reference Sabitbek34]).
In order to prove Theorem 2.1, we need two ingredients:
(i) The non-negative solution of the following equation
(2.7) \begin{equation}
\sum_{i,j=1}^n \frac{\partial }{\partial x_j} \left( W(|x|) |\nabla v|^{p-2}_A a_{ij}(x) \frac{\partial v}{\partial x_i} \right) + |\nabla d|^p_AH(|x|) v^{p-1} =0,
\end{equation}
\begin{equation}
\sum_{i,j=1}^n \frac{\partial }{\partial x_j} \left( W(|x|) |\nabla v|^{p-2}_A a_{ij}(x) \frac{\partial v}{\partial x_i} \right) + |\nabla d|^p_AH(|x|) v^{p-1} =0,
\end{equation}(ii) The (first-order) Picone identity with A(x) which is an n × n symmetric, uniformly positive definite matrix defined on Ω. Lemma 2.4 is similar to the standard Picone identity obtained by Allegretto-Huang [Reference Allegretto and Huang3] and the authors [Reference Ruzhansky, Sabitbek and Suragan26].
Let us start by transforming Equation (2.7) into a quasilinear second-order differential equation:
here the notation ![]() $' = \partial_{r}$ denotes the derivative with respect to r, and we define
$' = \partial_{r}$ denotes the derivative with respect to r, and we define ![]() $r:=d(x)$. The next theorem provides an explicit existence criterion of positive solution for ordinary differential Equation (2.8) which is proved by Agarwal-Bohner-Li [Reference Agarwal, Bohner and Li2, Theorem 4.6.13]:
$r:=d(x)$. The next theorem provides an explicit existence criterion of positive solution for ordinary differential Equation (2.8) which is proved by Agarwal-Bohner-Li [Reference Agarwal, Bohner and Li2, Theorem 4.6.13]:
Theorem 2.3. (Agarwal-Bohner-Li [Reference Agarwal, Bohner and Li2])
Let ![]() $a:[r_0, \infty) \rightarrow (0,\infty)$ and
$a:[r_0, \infty) \rightarrow (0,\infty)$ and ![]() $b:[r_0, \infty) \rightarrow (0,\infty)$ be continuous functions with
$b:[r_0, \infty) \rightarrow (0,\infty)$ be continuous functions with ![]() $b(r) \neq 0$. Suppose that
$b(r) \neq 0$. Suppose that
 \begin{equation*}
\int_{r_0}^{\infty} b(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} b(s)ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0.
\end{equation*}
\begin{equation*}
\int_{r_0}^{\infty} b(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} b(s)ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0.
\end{equation*}Suppose further that
 \begin{equation}
\int_{r_0}^{\infty} \left( \frac{\phi(s)}{a(s)}\right)^{\frac{1}{p-1}} ds \leq \frac{1}{2(p-1)}.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \left( \frac{\phi(s)}{a(s)}\right)^{\frac{1}{p-1}} ds \leq \frac{1}{2(p-1)}.
\end{equation}Then, there exists a non-negative solution to the following equation:
This transformation is based on the premise that W(x), H(x), and v(x) are positive radially symmetric functions. Let us rewrite the first term of (2.7) in terms of the radial derivative. First note that for ![]() $i,j=1,\ldots,n$, we have
$i,j=1,\ldots,n$, we have
 \begin{align}
\frac{\partial r}{\partial x_i} &= \left(\frac{p-1}{p-Q}\right) \Phi_p^{\frac{p-1}{p-Q}-1} \frac{\partial \Phi_p}{\partial x_i},
\end{align}
\begin{align}
\frac{\partial r}{\partial x_i} &= \left(\frac{p-1}{p-Q}\right) \Phi_p^{\frac{p-1}{p-Q}-1} \frac{\partial \Phi_p}{\partial x_i},
\end{align} \begin{align}
\frac{\partial r}{\partial x_j} \frac{\partial r}{\partial x_i} &= \left(\frac{p-1}{p-Q}\right)^2 \Phi_p^{2\frac{p-1}{p-Q}-2} \frac{\partial \Phi_p}{\partial x_i}\frac{\partial \Phi_p}{\partial x_j},
\end{align}
\begin{align}
\frac{\partial r}{\partial x_j} \frac{\partial r}{\partial x_i} &= \left(\frac{p-1}{p-Q}\right)^2 \Phi_p^{2\frac{p-1}{p-Q}-2} \frac{\partial \Phi_p}{\partial x_i}\frac{\partial \Phi_p}{\partial x_j},
\end{align} \begin{align}
\frac{\partial^2 r}{\partial x_i \partial x_j} &= \left(\frac{p-1}{p-Q}\right) \Phi_p^{\frac{p-1}{p-Q}-1} \frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} + \frac{(p-1)(Q-1)}{(p-Q)^2} \Phi_p^{\frac{p-1}{p-Q}-2} \frac{\partial \Phi_p}{\partial x_i}\frac{\partial \Phi_p}{\partial x_j}\\
&= \left(\frac{p-1}{p-Q}\right) \Phi_p^{\frac{p-1}{p-Q}-1} \frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} + \left(\frac{Q-1}{p-1}\right)\Phi_p^{-\frac{p-1}{p-Q}}\frac{\partial r}{\partial x_j} \frac{\partial r}{\partial x_i}. \nonumber
\end{align}
\begin{align}
\frac{\partial^2 r}{\partial x_i \partial x_j} &= \left(\frac{p-1}{p-Q}\right) \Phi_p^{\frac{p-1}{p-Q}-1} \frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} + \frac{(p-1)(Q-1)}{(p-Q)^2} \Phi_p^{\frac{p-1}{p-Q}-2} \frac{\partial \Phi_p}{\partial x_i}\frac{\partial \Phi_p}{\partial x_j}\\
&= \left(\frac{p-1}{p-Q}\right) \Phi_p^{\frac{p-1}{p-Q}-1} \frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} + \left(\frac{Q-1}{p-1}\right)\Phi_p^{-\frac{p-1}{p-Q}}\frac{\partial r}{\partial x_j} \frac{\partial r}{\partial x_i}. \nonumber
\end{align}Then
 \begin{align*}
\frac{\partial v}{\partial x_i} = v' \frac{\partial r}{\partial x_i}, \,\,\, \text{and} \,\,\, \frac{\partial^2 v}{\partial x_i \partial x_j} = \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j} v'' + \frac{\partial^2 r }{\partial x_i \partial x_j} v'.
\end{align*}
\begin{align*}
\frac{\partial v}{\partial x_i} = v' \frac{\partial r}{\partial x_i}, \,\,\, \text{and} \,\,\, \frac{\partial^2 v}{\partial x_i \partial x_j} = \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j} v'' + \frac{\partial^2 r }{\partial x_i \partial x_j} v'.
\end{align*} Since  $\Phi_p = r^{\frac{p-Q}{p-1}}$, we thus have
$\Phi_p = r^{\frac{p-Q}{p-1}}$, we thus have
 \begin{align}
|\nabla r|^{p-2}_A &=\left( \frac{p-1}{p-Q}\right)^{p-2} |\nabla \Phi_p|_A^{p-2} r^{\frac{(Q-1)(p-2)}{p-1}},
\end{align}
\begin{align}
|\nabla r|^{p-2}_A &=\left( \frac{p-1}{p-Q}\right)^{p-2} |\nabla \Phi_p|_A^{p-2} r^{\frac{(Q-1)(p-2)}{p-1}},
\end{align} \begin{align}
|\nabla v|^{p-2}_A &=|\nabla r|^{p-2}_A ( v')^{p-2},
\end{align}
\begin{align}
|\nabla v|^{p-2}_A &=|\nabla r|^{p-2}_A ( v')^{p-2},
\end{align} \begin{align}
\frac{\partial |\nabla v|^{p-2}_A}{\partial x_j}& = \frac{(Q-1)(p-2)}{(p-1)r}|\nabla r|^{p-2}_A (v')^{p-2} \frac{\partial r}{\partial x_j} + (p-2)|\nabla r|^{p-2}_A (v')^{p-3} v'' \frac{\partial r}{\partial x_j} \\
& +\left( \frac{p-1}{p-Q}\right)^{p-2} \frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}r^{\frac{(Q-1)(p-2)}{p-1}}(v')^{p-2}.\nonumber
\end{align}
\begin{align}
\frac{\partial |\nabla v|^{p-2}_A}{\partial x_j}& = \frac{(Q-1)(p-2)}{(p-1)r}|\nabla r|^{p-2}_A (v')^{p-2} \frac{\partial r}{\partial x_j} + (p-2)|\nabla r|^{p-2}_A (v')^{p-3} v'' \frac{\partial r}{\partial x_j} \\
& +\left( \frac{p-1}{p-Q}\right)^{p-2} \frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}r^{\frac{(Q-1)(p-2)}{p-1}}(v')^{p-2}.\nonumber
\end{align}Using above expressions, a straightforward computation gives:
 \begin{align*}
&\frac{\partial}{\partial {x_j}} \left( W a_{ij}(x)|\nabla v|^{p-2}_A \frac{\partial v}{\partial x_i} \right) = W a_{ij}(x)|\nabla v|^{p-2}_A \frac{\partial^2 v}{\partial x_i\partial x_j} \\
& + a_{ij}(x) |\nabla v|^{p-2}_A \frac{\partial W}{\partial x_j}\frac{\partial v}{\partial x_i} + W |\nabla v|^{p-2}_A \frac{\partial a_{ij}(x)}{\partial x_j}\frac{\partial v}{\partial x_i} + a_{ij}(x)W\frac{\partial |\nabla v|^{p-2}_A }{\partial x_j} \frac{\partial v}{\partial x_i},
\end{align*}
\begin{align*}
&\frac{\partial}{\partial {x_j}} \left( W a_{ij}(x)|\nabla v|^{p-2}_A \frac{\partial v}{\partial x_i} \right) = W a_{ij}(x)|\nabla v|^{p-2}_A \frac{\partial^2 v}{\partial x_i\partial x_j} \\
& + a_{ij}(x) |\nabla v|^{p-2}_A \frac{\partial W}{\partial x_j}\frac{\partial v}{\partial x_i} + W |\nabla v|^{p-2}_A \frac{\partial a_{ij}(x)}{\partial x_j}\frac{\partial v}{\partial x_i} + a_{ij}(x)W\frac{\partial |\nabla v|^{p-2}_A }{\partial x_j} \frac{\partial v}{\partial x_i},
\end{align*} \begin{align*}
&= W |\nabla r|^{p-2}_A ( v')^{p-2} v''\underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} + \left(\frac{p-1}{p-Q}\right) W |\nabla r|^{p-2}_A ( v')^{p-1} \Phi_p^{\frac{p-1}{p-Q}-1}\nonumber \\ & \qquad\quad a_{ij}(x) \frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} \\
&+ \left(\frac{Q-1}{p-1}\right) W |\nabla r|^{p-2}_A ( v')^{p-2}\Phi_p^{-\frac{p-1}{p-Q}}\underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} +|\nabla r|^{p-2}_A ( v')^{p-1}W_r \underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} \\
& + W |\nabla r|^{p-2}_A ( v')^{p-2} \frac{\partial a_{ij}(x)}{\partial x_j} v'\frac{\partial r}{\partial x_i} + \left( \frac{p-1}{p-Q}\right)^{p-2} W r^{\frac{(Q-1)(p-2)}{p-1}}(v')^{p-1}a_{ij}(x)\\ & \qquad \frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}\frac{\partial r}{\partial x_i}\\
& + \frac{(Q-1)(p-2)}{(p-1)r}|\nabla r|^{p-2}_A (v')^{p-1} \underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} + (p-2)W|\nabla r|^{p-2}_A (v')^{p-2} v''\\ & \qquad \underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A}
\end{align*}
\begin{align*}
&= W |\nabla r|^{p-2}_A ( v')^{p-2} v''\underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} + \left(\frac{p-1}{p-Q}\right) W |\nabla r|^{p-2}_A ( v')^{p-1} \Phi_p^{\frac{p-1}{p-Q}-1}\nonumber \\ & \qquad\quad a_{ij}(x) \frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} \\
&+ \left(\frac{Q-1}{p-1}\right) W |\nabla r|^{p-2}_A ( v')^{p-2}\Phi_p^{-\frac{p-1}{p-Q}}\underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} +|\nabla r|^{p-2}_A ( v')^{p-1}W_r \underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} \\
& + W |\nabla r|^{p-2}_A ( v')^{p-2} \frac{\partial a_{ij}(x)}{\partial x_j} v'\frac{\partial r}{\partial x_i} + \left( \frac{p-1}{p-Q}\right)^{p-2} W r^{\frac{(Q-1)(p-2)}{p-1}}(v')^{p-1}a_{ij}(x)\\ & \qquad \frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}\frac{\partial r}{\partial x_i}\\
& + \frac{(Q-1)(p-2)}{(p-1)r}|\nabla r|^{p-2}_A (v')^{p-1} \underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A} + (p-2)W|\nabla r|^{p-2}_A (v')^{p-2} v''\\ & \qquad \underbrace{a_{ij}(x) \frac{\partial r}{\partial x_i}\frac{\partial r}{\partial x_j}}_{=|\nabla r|^2_A}
\end{align*} where  $|\nabla r|^2_A = \sum_{i,j=1}^n \partial_{x_i}r \partial_{x_j}r$. We assume there is the summation
$|\nabla r|^2_A = \sum_{i,j=1}^n \partial_{x_i}r \partial_{x_j}r$. We assume there is the summation  $\sum_{i,j=1}^n$, to get:
$\sum_{i,j=1}^n$, to get:
 \begin{align*}
&= W |\nabla r|^{p}_A ( v')^{p-2} \Biggl((p-1) v'' + \left(\frac{Q-1}{r}\right)\frac{1}{p-1} v'\nonumber \\
& \qquad \left. + \left(\frac{p-1}{p-Q}\right)\frac{\Phi_p^{\frac{p-1}{p-Q}-1}}{|\nabla r|_A^2} a_{ij}(x) \frac{\partial^2 \Phi_p}{\partial x_i \partial x_j} v'\right)\\
& + |\nabla r|_A^p (v')^{p-1}W_r + W|\nabla r|_A^{p-2}(v')^{p-1} \frac{\partial a_{ij}}{\partial x_j}\frac{\partial r}{\partial x_i} + \left(\frac{Q-1}{r}\right)\nonumber \\ & \qquad \left(1 - \frac{1}{p-1}\right)W |\nabla r|_A^p (v')^{p-1}\\
& + \underbrace{\left( \frac{p-1}{p-Q}\right)^{p-2} r^{\frac{(Q-1)(p-2)}{p-1}} |\nabla \Phi_p|^{p-2}_A}_{=|\nabla r|_A^{p-2}} \frac{W(v')^{p-1}a_{ij}(x)}{|\nabla \Phi_p|^{p-2}_A} \frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}\frac{\partial r}{\partial x_i}.
\end{align*}
\begin{align*}
&= W |\nabla r|^{p}_A ( v')^{p-2} \Biggl((p-1) v'' + \left(\frac{Q-1}{r}\right)\frac{1}{p-1} v'\nonumber \\
& \qquad \left. + \left(\frac{p-1}{p-Q}\right)\frac{\Phi_p^{\frac{p-1}{p-Q}-1}}{|\nabla r|_A^2} a_{ij}(x) \frac{\partial^2 \Phi_p}{\partial x_i \partial x_j} v'\right)\\
& + |\nabla r|_A^p (v')^{p-1}W_r + W|\nabla r|_A^{p-2}(v')^{p-1} \frac{\partial a_{ij}}{\partial x_j}\frac{\partial r}{\partial x_i} + \left(\frac{Q-1}{r}\right)\nonumber \\ & \qquad \left(1 - \frac{1}{p-1}\right)W |\nabla r|_A^p (v')^{p-1}\\
& + \underbrace{\left( \frac{p-1}{p-Q}\right)^{p-2} r^{\frac{(Q-1)(p-2)}{p-1}} |\nabla \Phi_p|^{p-2}_A}_{=|\nabla r|_A^{p-2}} \frac{W(v')^{p-1}a_{ij}(x)}{|\nabla \Phi_p|^{p-2}_A} \frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}\frac{\partial r}{\partial x_i}.
\end{align*} Now, we apply Equation (2.11) for ![]() $\partial r / \partial x_i$
$\partial r / \partial x_i$
 \begin{align*}
&=W |\nabla r|_A^p (v')^{p-2}\left( (p-1) v'' + \left[\frac{Q-1}{r} + \frac{W_r}{W}\right] v'\right)\nonumber \\ & \qquad + \left(\frac{p-1}{p-Q} \right)W |\nabla r|_A^{p-2} (v')^{p-1}\Phi_p^{\frac{p-1}{p-Q}-1}\\
& \times \frac{1}{|\nabla \Phi_p|^{p-2}_A}\nonumber \\ & \qquad \underbrace{\sum_{i,j=1}^n\left[|\nabla \Phi_p|^{p-2}_Aa_{ij}(x)\frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} + a_{ij}(x)\frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}\frac{\partial \Phi_p}{\partial x_i} + |\nabla \Phi_p|^{p-2}_A\frac{\partial a_{ij}}{\partial x_j}\frac{\partial \Phi_p}{\partial x_i}\right]}_{\mathcal{L}_{p,A}\Phi_p(x)=0} \\
& = W (r)|\nabla r|_A^p (v')^{p-2}\left( (p-1) v'' + \left[\frac{Q-1}{r} + \frac{W_r}{W}\right] v'\right).
\end{align*}
\begin{align*}
&=W |\nabla r|_A^p (v')^{p-2}\left( (p-1) v'' + \left[\frac{Q-1}{r} + \frac{W_r}{W}\right] v'\right)\nonumber \\ & \qquad + \left(\frac{p-1}{p-Q} \right)W |\nabla r|_A^{p-2} (v')^{p-1}\Phi_p^{\frac{p-1}{p-Q}-1}\\
& \times \frac{1}{|\nabla \Phi_p|^{p-2}_A}\nonumber \\ & \qquad \underbrace{\sum_{i,j=1}^n\left[|\nabla \Phi_p|^{p-2}_Aa_{ij}(x)\frac{\partial^2 \Phi_p}{\partial x_i\partial x_j} + a_{ij}(x)\frac{\partial |\nabla \Phi_p|_A^{p-2}}{\partial x_j}\frac{\partial \Phi_p}{\partial x_i} + |\nabla \Phi_p|^{p-2}_A\frac{\partial a_{ij}}{\partial x_j}\frac{\partial \Phi_p}{\partial x_i}\right]}_{\mathcal{L}_{p,A}\Phi_p(x)=0} \\
& = W (r)|\nabla r|_A^p (v')^{p-2}\left( (p-1) v'' + \left[\frac{Q-1}{r} + \frac{W_r}{W}\right] v'\right).
\end{align*}We conclude that (2.7) can be rewritten as:
 \begin{equation}
W (r)|\nabla r|_A^p (v')^{p-2}\left( (p-1) v'' + \left[\frac{Q-1}{r} + \frac{W_r}{W}\right] v'\right) + |\nabla r|_A^pH(r) v^{p-1} =0,
\end{equation}
\begin{equation}
W (r)|\nabla r|_A^p (v')^{p-2}\left( (p-1) v'' + \left[\frac{Q-1}{r} + \frac{W_r}{W}\right] v'\right) + |\nabla r|_A^pH(r) v^{p-1} =0,
\end{equation} which means ![]() $(r^{Q-1} W(r) (v'(r))^{p-1})' + r^{Q-1}H(r) v^{p-1}(r) =0,$ which is (2.8).
$(r^{Q-1} W(r) (v'(r))^{p-1})' + r^{Q-1}H(r) v^{p-1}(r) =0,$ which is (2.8).
The next key element in our analysis is the first-order Picone identity.
Lemma 2.4. Let Ω be a bounded domain in ![]() $\mathbb{R}^n$. Let a complex-valued function u be differentiable a.e. in Ω. Let
$\mathbb{R}^n$. Let a complex-valued function u be differentiable a.e. in Ω. Let ![]() $1 \lt p \lt \infty$. Let a positive function v be differentiable in Ω. Define
$1 \lt p \lt \infty$. Let a positive function v be differentiable in Ω. Define
 \begin{align}
R(u,v) &= |\nabla u|^p_A - \langle A(x)\nabla\left(\frac{|u|^p}{v^{p-1}} \right),|\nabla v|^{p-2}_A\nabla v\rangle,
\end{align}
\begin{align}
R(u,v) &= |\nabla u|^p_A - \langle A(x)\nabla\left(\frac{|u|^p}{v^{p-1}} \right),|\nabla v|^{p-2}_A\nabla v\rangle,
\end{align} \begin{align}
L(u,v) &= |\nabla u|^p_A -p\frac{|u|^{p-1} }{v^{p-1}}|\nabla v|^{p-2}_A \langle A(x)\nabla|u|, \nabla v \rangle + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A,
\end{align}
\begin{align}
L(u,v) &= |\nabla u|^p_A -p\frac{|u|^{p-1} }{v^{p-1}}|\nabla v|^{p-2}_A \langle A(x)\nabla|u|, \nabla v \rangle + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A,
\end{align} where ![]() $|\xi|^2_A= \langle A(x)\xi,\xi\rangle$. Then
$|\xi|^2_A= \langle A(x)\xi,\xi\rangle$. Then
Moreover, ![]() $L(u,v)=0$ a.e. in Ω if and only if
$L(u,v)=0$ a.e. in Ω if and only if ![]() $u\geq 0$ and u = cv a.e. in Ω for some constant c in each component of Ω.
$u\geq 0$ and u = cv a.e. in Ω for some constant c in each component of Ω.
Proof of Lemma 2.4
It is easy to show that ![]() $R(u,v)=L(u,v)$ by the expansion of
$R(u,v)=L(u,v)$ by the expansion of ![]() $R(u,v)$ as follows:
$R(u,v)$ as follows:
 \begin{align*}
R(u,v) &= |\nabla u|^p_A - \langle A(x)\nabla\left(\frac{|u|^p}{v^{p-1}} \right),|\nabla v|^{p-2}_A\nabla v \rangle \\
& = |\nabla u|^p_A -p\frac{|u|^{p-1} }{v^{p-1}}|\nabla v|^{p-2}_A \langle A(x) \nabla|u|, \nabla v\rangle + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A\\
& = L(u,v).
\end{align*}
\begin{align*}
R(u,v) &= |\nabla u|^p_A - \langle A(x)\nabla\left(\frac{|u|^p}{v^{p-1}} \right),|\nabla v|^{p-2}_A\nabla v \rangle \\
& = |\nabla u|^p_A -p\frac{|u|^{p-1} }{v^{p-1}}|\nabla v|^{p-2}_A \langle A(x) \nabla|u|, \nabla v\rangle + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A\\
& = L(u,v).
\end{align*} Let ![]() $u(x)=R(x)+iI(x)$, where R(x) and I(x) are the real and imaginary parts of u. We can restrict to the set where
$u(x)=R(x)+iI(x)$, where R(x) and I(x) are the real and imaginary parts of u. We can restrict to the set where ![]() $u(x)\neq 0$. Then, we have
$u(x)\neq 0$. Then, we have
 \begin{align}
(\nabla |u|)(x) = \frac{1}{|u|} (R(x)\nabla R(x)+ I(x) \nabla I(x)).
\end{align}
\begin{align}
(\nabla |u|)(x) = \frac{1}{|u|} (R(x)\nabla R(x)+ I(x) \nabla I(x)).
\end{align}Since
 \begin{align*}
\left| \frac{1}{|u|} (R\nabla R+ I \nabla I) \right|^2_A \leq |\nabla R|^2_A + |\nabla I|^2_A,
\end{align*}
\begin{align*}
\left| \frac{1}{|u|} (R\nabla R+ I \nabla I) \right|^2_A \leq |\nabla R|^2_A + |\nabla I|^2_A,
\end{align*} we get ![]() $|\nabla |u||_A\leq |\nabla u|_A$ a.e. in Ω (see [Reference Ruzhansky, Sabitbek and Suragan25, Theorem 2.1]).
$|\nabla |u||_A\leq |\nabla u|_A$ a.e. in Ω (see [Reference Ruzhansky, Sabitbek and Suragan25, Theorem 2.1]).
Let us recall Young’s inequality where for real numbers a and b we have
 \begin{equation*}
p ab \leq a^p + (p-1)b^{\frac{p}{p-1}}.
\end{equation*}
\begin{equation*}
p ab \leq a^p + (p-1)b^{\frac{p}{p-1}}.
\end{equation*} By taking ![]() $a=|\nabla u|_A$ and
$a=|\nabla u|_A$ and  $b=\frac{|u|^{p-1}}{v^{p-1}}|\nabla v|_A^{p-1}$, we prove
$b=\frac{|u|^{p-1}}{v^{p-1}}|\nabla v|_A^{p-1}$, we prove ![]() $L(u,v)\geq 0$ in the following way:
$L(u,v)\geq 0$ in the following way:
 \begin{align*}
L(u,v)& = |\nabla u|^p_A -p\frac{|u|^{p-1} }{v^{p-1}}|\nabla v|^{p-2}_A \langle A(x) \nabla|u|,\nabla v\rangle + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A\\
& = |\nabla u|^p_A -p\frac{|u|^{p-1}}{v^{p-1}}|\nabla |u||_A|\nabla v|^{p-1}_A + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A \\
& + p\frac{|u|^{p-1}|\nabla v|^{p-2}_A}{v^{p-1}} \left( |\nabla |u||_A|\nabla v|_A -\langle A(x)\nabla |u|, \nabla v\rangle \right) \\
& \geq |\nabla u|^p_A -p\frac{|u|^{p-1}}{v^{p-1}}|\nabla u|_A|\nabla v|^{p-1}_A + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A \\
& + p\frac{|u|^{p-1}|\nabla v|^{p-2}_A}{v^{p-1}} \left( |\nabla |u||_A|\nabla v|_A - \langle A(x)\nabla |u|, \nabla v\rangle \right)\\
& \geq p\frac{|u|^{p-1}|\nabla v|^{p-2}_A}{v^{p-1}} \left( |\nabla |u||_A|\nabla v|_A - \langle A(x)\nabla |u|, \nabla v\rangle \right).
\end{align*}
\begin{align*}
L(u,v)& = |\nabla u|^p_A -p\frac{|u|^{p-1} }{v^{p-1}}|\nabla v|^{p-2}_A \langle A(x) \nabla|u|,\nabla v\rangle + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A\\
& = |\nabla u|^p_A -p\frac{|u|^{p-1}}{v^{p-1}}|\nabla |u||_A|\nabla v|^{p-1}_A + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A \\
& + p\frac{|u|^{p-1}|\nabla v|^{p-2}_A}{v^{p-1}} \left( |\nabla |u||_A|\nabla v|_A -\langle A(x)\nabla |u|, \nabla v\rangle \right) \\
& \geq |\nabla u|^p_A -p\frac{|u|^{p-1}}{v^{p-1}}|\nabla u|_A|\nabla v|^{p-1}_A + (p-1)\frac{|u|^p}{v^p}|\nabla v|^p_A \\
& + p\frac{|u|^{p-1}|\nabla v|^{p-2}_A}{v^{p-1}} \left( |\nabla |u||_A|\nabla v|_A - \langle A(x)\nabla |u|, \nabla v\rangle \right)\\
& \geq p\frac{|u|^{p-1}|\nabla v|^{p-2}_A}{v^{p-1}} \left( |\nabla |u||_A|\nabla v|_A - \langle A(x)\nabla |u|, \nabla v\rangle \right).
\end{align*} We will now show that ![]() $|\nabla |u||_A|\nabla v|_A \geq\langle A(x)\nabla |u|, \nabla v\rangle $, which implies
$|\nabla |u||_A|\nabla v|_A \geq\langle A(x)\nabla |u|, \nabla v\rangle $, which implies ![]() $L(u,v)\geq 0$. A direct computation gives
$L(u,v)\geq 0$. A direct computation gives
 \begin{align*}
0 \leq | \nabla |u| - b\nabla v |^2_A &= \langle A(x) (\nabla |u| - b\nabla v), \nabla |u| - b\nabla v \rangle \\
& =|\nabla |u||^2_A -2b\langle A(x) \nabla |u|,\nabla v\rangle + b^2 |\nabla v|^2_A.
\end{align*}
\begin{align*}
0 \leq | \nabla |u| - b\nabla v |^2_A &= \langle A(x) (\nabla |u| - b\nabla v), \nabla |u| - b\nabla v \rangle \\
& =|\nabla |u||^2_A -2b\langle A(x) \nabla |u|,\nabla v\rangle + b^2 |\nabla v|^2_A.
\end{align*} Setting  $b=|\nabla v|_A^{-2} \langle A(x)\nabla |u|,\nabla v\rangle$ and rearranging produces
$b=|\nabla v|_A^{-2} \langle A(x)\nabla |u|,\nabla v\rangle$ and rearranging produces
Observe that ![]() $L(u,v)=0$ if and only if
$L(u,v)=0$ if and only if
• equality holds for
 $|\nabla |u||_A \leq |\nabla u|_A$ when
$|\nabla |u||_A \leq |\nabla u|_A$ when  $u\geq 0$;
$u\geq 0$;• equality holds in (2.21) when u = cv for some constant c.
The proof is complete.
Proof of Theorem 2.1
By Theorem 2.3, the conditions (2.5) and (2.6) provide the existence of a non-negative solution to the following equation
 \begin{equation}
\nabla \cdot (W(x) |\nabla v|^{p-2}_A A(x)\nabla v)+ |\nabla d|^p_A(x)H(x) v^{p-1} = 0.
\end{equation}
\begin{equation}
\nabla \cdot (W(x) |\nabla v|^{p-2}_A A(x)\nabla v)+ |\nabla d|^p_A(x)H(x) v^{p-1} = 0.
\end{equation}Then, we prove by applying properties of the (first-order) Picone identity, divergence theorem and the Equation (2.22), respectively. We have
 \begin{align*}
0&\leq \int_{\Omega} W(x) R(u,v) dx\\
&= \int_{\Omega} W(x)|\nabla u|^p_A dx - \int_{\Omega} W(x) \langle A(x)\nabla\left(\frac{|u|^p}{v^{p-1}} \right), |\nabla v|^{p-2}_A\nabla v \rangle dx \\
& = \int_{\Omega} W(x)|\nabla u|^p_A - \int_{\Omega} |\nabla d|^p_AH(x) |u|^p dx.
\end{align*}
\begin{align*}
0&\leq \int_{\Omega} W(x) R(u,v) dx\\
&= \int_{\Omega} W(x)|\nabla u|^p_A dx - \int_{\Omega} W(x) \langle A(x)\nabla\left(\frac{|u|^p}{v^{p-1}} \right), |\nabla v|^{p-2}_A\nabla v \rangle dx \\
& = \int_{\Omega} W(x)|\nabla u|^p_A - \int_{\Omega} |\nabla d|^p_AH(x) |u|^p dx.
\end{align*}This proves Theorem 2.1.
Next, we will give examples for operators ![]() $\mathcal{L}_A$ by taking different matrices A(x).
$\mathcal{L}_A$ by taking different matrices A(x).
Euclidean Space ![]() $\mathbb{R}^n$: Let
$\mathbb{R}^n$: Let ![]() $\Omega = \mathbb{R}^n$. If we take A(x) as an identity matrix, then
$\Omega = \mathbb{R}^n$. If we take A(x) as an identity matrix, then ![]() $\mathcal{L}_A = - \Delta$ is the standard Laplacian,
$\mathcal{L}_A = - \Delta$ is the standard Laplacian, ![]() $\Phi(x)= |x|^{2-n}$ and
$\Phi(x)= |x|^{2-n}$ and ![]() $d(x) = |x|$ with
$d(x) = |x|$ with ![]() $x \in \mathbb{R}^n$.
$x \in \mathbb{R}^n$.
Corollary 2.5. Let ![]() $\Omega = \mathbb{R}^n$. Let
$\Omega = \mathbb{R}^n$. Let ![]() $W(|x|)$ and
$W(|x|)$ and ![]() $H(|x|)$ be positive radially symmetric functions. Then the inequality
$H(|x|)$ be positive radially symmetric functions. Then the inequality
 \begin{equation}
\int_{\mathbb{R}^n} W(|x|) |\nabla u|^2 dx \geq \int_{\mathbb{R}^n} H(|x|) |u|^2 dx
\end{equation}
\begin{equation}
\int_{\mathbb{R}^n} W(|x|) |\nabla u|^2 dx \geq \int_{\mathbb{R}^n} H(|x|) |u|^2 dx
\end{equation} holds for all complex-valued functions ![]() $u \in C^1_0(\Omega)$ provided that the following conditions hold:
$u \in C^1_0(\Omega)$ provided that the following conditions hold:
 \begin{equation}
\int_{r_0}^{\infty} s^{n-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{n-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} s^{n-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{n-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation} \begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{n-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{n-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation} The Heisenberg group ![]() $\mathbb{H}^1$: Let
$\mathbb{H}^1$: Let ![]() $\mathbb{H}^1:= \mathbb{R}^2 \times \mathbb{R}$ be Heisenberg group with
$\mathbb{H}^1:= \mathbb{R}^2 \times \mathbb{R}$ be Heisenberg group with ![]() $x = (x_1,x_2,x_3)$. We take
$x = (x_1,x_2,x_3)$. We take
 \begin{equation*}A(x):=\begin{pmatrix}
1 & 0 & -\frac{x_2}{2}\\ 0 & 1 & \frac{x_1}{2}\\
-\frac{x_2}{2} & \frac{x_1}{2} & \frac{x_1^2 + x_2^2}{4}
\end{pmatrix}.\end{equation*}
\begin{equation*}A(x):=\begin{pmatrix}
1 & 0 & -\frac{x_2}{2}\\ 0 & 1 & \frac{x_1}{2}\\
-\frac{x_2}{2} & \frac{x_1}{2} & \frac{x_1^2 + x_2^2}{4}
\end{pmatrix}.\end{equation*}Then, we have the following horizontal gradient
 \begin{equation*}\nabla_{\mathbb{H}}:= (\partial_{x_1} - \frac{x_2}{2} \partial_{x_3}, \partial_{x_2} + \frac{x_1}{2} \partial_{x_3}),\end{equation*}
\begin{equation*}\nabla_{\mathbb{H}}:= (\partial_{x_1} - \frac{x_2}{2} \partial_{x_3}, \partial_{x_2} + \frac{x_1}{2} \partial_{x_3}),\end{equation*}and the sub-Laplacian is given by:
 \begin{equation*}
\mathcal{L}_{\mathbb{H}} := \Delta_{x_1,x_2} + \frac{x_1^2 + x_2^2}{4} \partial_{x_3}^2 + (x_1\partial_{x_2} - x_2 \partial_{x_1})\partial_{x_3}.
\end{equation*}
\begin{equation*}
\mathcal{L}_{\mathbb{H}} := \Delta_{x_1,x_2} + \frac{x_1^2 + x_2^2}{4} \partial_{x_3}^2 + (x_1\partial_{x_2} - x_2 \partial_{x_1})\partial_{x_3}.
\end{equation*} The quasi-norm (![]() $\mathcal{L}$-gauge) is given by:
$\mathcal{L}$-gauge) is given by:  $
d_{\mathbb{H}}(x) = ( (x_1^2+x_2^2)^2 + 16 x_3^2 )^{\frac{1}{4}}.
$ Note that the function
$
d_{\mathbb{H}}(x) = ( (x_1^2+x_2^2)^2 + 16 x_3^2 )^{\frac{1}{4}}.
$ Note that the function ![]() $\Psi_{\mathcal{L}_{\mathbb{H}}}(x)$ could be explicitly calculated as follow:
$\Psi_{\mathcal{L}_{\mathbb{H}}}(x)$ could be explicitly calculated as follow:
 \begin{align*}
\Psi_{\mathcal{L}_{\mathbb{H}}}(x) = |\nabla_{\mathbb{H}} d_{\mathbb{H}}|^2(x) &= (X_1d_{\mathbb{H}})^2+ (X_2d_{\mathbb{H}})^2 \\
& = d_{\mathbb{H}}^{-6} [(x_1^2+x_2^2)^2 x_1^2 - 8 (x_1^2+x_2^2)x_1x_2x_3 + 16x_1^2x_3^2] \\
& + d_{\mathbb{H}}^{-6} [(x_1^2+x_2^2)^2 x_2^2 + 8 (x_1^2+x_2^2)x_1x_2x_3 + 16x_2^2x_3^2] \\
& = d_{\mathbb{H}}^{-6}(x_1^2+x_2^2)[(x_1^2+x_2^2)^2 + 16x_3^2] = |x'|^2 d_{\mathbb{H}}^{-2}(x),
\end{align*}
\begin{align*}
\Psi_{\mathcal{L}_{\mathbb{H}}}(x) = |\nabla_{\mathbb{H}} d_{\mathbb{H}}|^2(x) &= (X_1d_{\mathbb{H}})^2+ (X_2d_{\mathbb{H}})^2 \\
& = d_{\mathbb{H}}^{-6} [(x_1^2+x_2^2)^2 x_1^2 - 8 (x_1^2+x_2^2)x_1x_2x_3 + 16x_1^2x_3^2] \\
& + d_{\mathbb{H}}^{-6} [(x_1^2+x_2^2)^2 x_2^2 + 8 (x_1^2+x_2^2)x_1x_2x_3 + 16x_2^2x_3^2] \\
& = d_{\mathbb{H}}^{-6}(x_1^2+x_2^2)[(x_1^2+x_2^2)^2 + 16x_3^2] = |x'|^2 d_{\mathbb{H}}^{-2}(x),
\end{align*} where ![]() $|x'|^2 = x_1^2+ x_2^2$.
$|x'|^2 = x_1^2+ x_2^2$.
Corollary 2.6. Let Ω bounded domain in ![]() $\mathbb{H}^1$. Let W(x) and H(x) be positive radially symmetric functions. Then, the inequality
$\mathbb{H}^1$. Let W(x) and H(x) be positive radially symmetric functions. Then, the inequality
 \begin{equation}
\int_{\Omega} W(x) |\nabla_{\mathbb{H}} u|^2 dx \geq \int_{\Omega} |\nabla_{\mathbb{H}} d_{\mathbb{H}}|^2 H(x) |u|^2 dx,
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\nabla_{\mathbb{H}} u|^2 dx \geq \int_{\Omega} |\nabla_{\mathbb{H}} d_{\mathbb{H}}|^2 H(x) |u|^2 dx,
\end{equation} holds for all complex-valued functions ![]() $u \in C^1_0(\Omega)$ provided that the following conditions hold:
$u \in C^1_0(\Omega)$ provided that the following conditions hold:
 \begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation} \begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation} Baouendi–Grushin operator: Let Ω be an open subset of ![]() $\mathbb{R}^n=\mathbb{R}^k\times \mathbb{R}^l$ and
$\mathbb{R}^n=\mathbb{R}^k\times \mathbb{R}^l$ and ![]() $x\in \Omega$ with
$x\in \Omega$ with ![]() $x = (\xi,\zeta)$. For γ > 0, we take
$x = (\xi,\zeta)$. For γ > 0, we take
 \begin{equation*}A(x):=\begin{pmatrix}
I_k & 0\\ 0 &\gamma|\xi|^{\gamma}I_l,
\end{pmatrix},\end{equation*}
\begin{equation*}A(x):=\begin{pmatrix}
I_k & 0\\ 0 &\gamma|\xi|^{\gamma}I_l,
\end{pmatrix},\end{equation*} where Ik and Il are the identity matrices of size k and l, respectively. Then, we have the following vector field ![]() $\nabla_{\gamma}:= (\nabla_{\xi}, \gamma|\xi|^{\gamma}\nabla_{\zeta})$ and the Baouendi–Grushin operator
$\nabla_{\gamma}:= (\nabla_{\xi}, \gamma|\xi|^{\gamma}\nabla_{\zeta})$ and the Baouendi–Grushin operator
 \begin{equation*}\mathcal{L}_{\gamma}:= -\Delta_{\xi}-\gamma^2|\xi|^{2\gamma}\Delta_{\zeta}.\end{equation*}
\begin{equation*}\mathcal{L}_{\gamma}:= -\Delta_{\xi}-\gamma^2|\xi|^{2\gamma}\Delta_{\zeta}.\end{equation*} For ![]() $x = (\xi,\zeta) \in \mathbb{R}^k\times \mathbb{R}^l$, let
$x = (\xi,\zeta) \in \mathbb{R}^k\times \mathbb{R}^l$, let ![]() $ d_{\gamma}(x) = (|\xi|^{2\gamma} + |\zeta|^2)^{1/2\gamma}$.
$ d_{\gamma}(x) = (|\xi|^{2\gamma} + |\zeta|^2)^{1/2\gamma}$.
As in the Heisenberg group, the function ![]() $\Psi_{\mathcal{L}_{\gamma}}(x)$ could be explicitly calculated as follow:
$\Psi_{\mathcal{L}_{\gamma}}(x)$ could be explicitly calculated as follow:
 \begin{align*}
\Psi_{\mathcal{L}_{\gamma}}(x) = |\nabla_{\gamma} d_{\gamma}|^2(x) &= \sum_{i=1}^k (\partial_{\xi_i} d_{\gamma})^2 + \sum_{i=1}^l \gamma^2|\xi|^{2\gamma}(\partial_{\zeta_i} d_{\gamma})^2 \\
& = (|\xi|^{2\gamma} + |\zeta|^2)^{\frac{1}{\gamma}-2} (|\xi|^{4\gamma} + |\xi|^{2\gamma}|\zeta|^2) = \frac{|\xi|^{2\gamma}}{d_{\gamma}^{2\gamma}(x)}.
\end{align*}
\begin{align*}
\Psi_{\mathcal{L}_{\gamma}}(x) = |\nabla_{\gamma} d_{\gamma}|^2(x) &= \sum_{i=1}^k (\partial_{\xi_i} d_{\gamma})^2 + \sum_{i=1}^l \gamma^2|\xi|^{2\gamma}(\partial_{\zeta_i} d_{\gamma})^2 \\
& = (|\xi|^{2\gamma} + |\zeta|^2)^{\frac{1}{\gamma}-2} (|\xi|^{4\gamma} + |\xi|^{2\gamma}|\zeta|^2) = \frac{|\xi|^{2\gamma}}{d_{\gamma}^{2\gamma}(x)}.
\end{align*}Corollary 2.7. Let Ω be an open subset of ![]() $\mathbb{R}^n=\mathbb{R}^k\times \mathbb{R}^l$ and
$\mathbb{R}^n=\mathbb{R}^k\times \mathbb{R}^l$ and ![]() $x\in \Omega$ with
$x\in \Omega$ with ![]() $x = (\xi,\zeta)$. Let W(x) and H(x) be positive radially symmetric functions. Then, the inequality:
$x = (\xi,\zeta)$. Let W(x) and H(x) be positive radially symmetric functions. Then, the inequality:
 \begin{equation}
\int_{\Omega} W(x) |\nabla_{\gamma} u|^2 dx \geq \int_{\Omega} |\nabla_{\gamma} d_{\gamma}|^{2} H(x) |u|^2 dx
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\nabla_{\gamma} u|^2 dx \geq \int_{\Omega} |\nabla_{\gamma} d_{\gamma}|^{2} H(x) |u|^2 dx
\end{equation} holds for all complex-valued functions ![]() $u \in C^1_0(\Omega)$ provided that the following conditions hold:
$u \in C^1_0(\Omega)$ provided that the following conditions hold:
 \begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s)ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s)ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation} \begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2}\,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2}\,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation} The Engel group ![]() $\mathbb{E}$: Let
$\mathbb{E}$: Let ![]() $\mathbb{E}:= \mathbb{R}^2 \times \mathbb{R}\times \mathbb{R}$ be the Engel group with
$\mathbb{E}:= \mathbb{R}^2 \times \mathbb{R}\times \mathbb{R}$ be the Engel group with ![]() $x = (x_1,x_2,x_3,x_4)$. We take
$x = (x_1,x_2,x_3,x_4)$. We take
 \begin{equation*}A(x):=\begin{pmatrix}
1 & 0 & -\frac{x_2}{2}& - \frac{x_3}{2} + \frac{x_1x_2}{12}\\ 0 & 1 & \frac{x_1}{2}& \frac{x_1^2}{12}\\
-\frac{x_2}{2} & \frac{x_1}{2} & \frac{x_1^2+x_2^2}{4} & \frac{x_2}{2}\left( \frac{x_3}{2} -\frac{x_1x_2}{12} \right) + \frac{x_1^3}{24} \\
- \frac{x_3}{2} + \frac{x_1x_2}{12}&\frac{x_1^2}{12}& \frac{x_2}{2}\left( \frac{x_3}{2} -\frac{x_1x_2}{12} \right) + \frac{x_1^3}{24} & \left( \frac{x_3}{2} -\frac{x_1x_2}{12} \right)^2 + \frac{x_1^4}{144}
\end{pmatrix}.\end{equation*}
\begin{equation*}A(x):=\begin{pmatrix}
1 & 0 & -\frac{x_2}{2}& - \frac{x_3}{2} + \frac{x_1x_2}{12}\\ 0 & 1 & \frac{x_1}{2}& \frac{x_1^2}{12}\\
-\frac{x_2}{2} & \frac{x_1}{2} & \frac{x_1^2+x_2^2}{4} & \frac{x_2}{2}\left( \frac{x_3}{2} -\frac{x_1x_2}{12} \right) + \frac{x_1^3}{24} \\
- \frac{x_3}{2} + \frac{x_1x_2}{12}&\frac{x_1^2}{12}& \frac{x_2}{2}\left( \frac{x_3}{2} -\frac{x_1x_2}{12} \right) + \frac{x_1^3}{24} & \left( \frac{x_3}{2} -\frac{x_1x_2}{12} \right)^2 + \frac{x_1^4}{144}
\end{pmatrix}.\end{equation*}Then the horizontal gradient and sub-Laplacian are given by:
where
 \begin{equation*}
X_1:= \partial_{x_1} - \frac{x_2}{2} \partial_{x_3} - \left(\frac{x_3}{2}-\frac{x_1x_2}{12}\right)\partial_{x_4}, \,\, \text{and} \,\, X_2:=\partial_{x_2} + \frac{x_1}{2} \partial_{x_3} + \frac{x_1^2}{12} \partial_{x_4}.
\end{equation*}
\begin{equation*}
X_1:= \partial_{x_1} - \frac{x_2}{2} \partial_{x_3} - \left(\frac{x_3}{2}-\frac{x_1x_2}{12}\right)\partial_{x_4}, \,\, \text{and} \,\, X_2:=\partial_{x_2} + \frac{x_1}{2} \partial_{x_3} + \frac{x_1^2}{12} \partial_{x_4}.
\end{equation*}Corollary 2.8. Let Ω be a bounded domain in ![]() $\mathbb{E}$. Let W(x) and H(x) be positive radially symmetric functions. Then the inequality
$\mathbb{E}$. Let W(x) and H(x) be positive radially symmetric functions. Then the inequality
 \begin{equation}
\int_{\Omega} W(x) |\nabla_{\mathbb{E}} u|^2 dx \geq \int_{\Omega} |\nabla_{\mathbb{E}} d|^2 H(x) |u|^2 dx
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\nabla_{\mathbb{E}} u|^2 dx \geq \int_{\Omega} |\nabla_{\mathbb{E}} d|^2 H(x) |u|^2 dx
\end{equation} holds for all complex-valued functions ![]() $u \in C^1_0(\Omega)$ provided that the following conditions hold:
$u \in C^1_0(\Omega)$ provided that the following conditions hold:
 \begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation} \begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation} The Cartan group ![]() $\mathcal{B}_5$: Let
$\mathcal{B}_5$: Let ![]() $\mathcal{B}_5:= \mathbb{R}^2 \times \mathbb{R}\times \mathbb{R}^2$ be the Cartan group with
$\mathcal{B}_5:= \mathbb{R}^2 \times \mathbb{R}\times \mathbb{R}^2$ be the Cartan group with ![]() $x = (x_1,x_2,x_3,x_4,x_5)$. We take
$x = (x_1,x_2,x_3,x_4,x_5)$. We take
 \begin{equation*}A(x):=\begin{pmatrix}
1 & 0 & 0& 0& 0\\
0 & 1 & -x_1& \frac{x_1^2}{2}& x_1x_2\\
0 & -x_1& x_1^2 & - \frac{x_1^3}{2} & -x_1^2x_2\\
0 & \frac{x_1^2}{2} & - \frac{x_1^3}{2} & \frac{x_1^4}{4} & \frac{x_1^3x_2}{2} \\
0 & x_1x_2 &-x_1^2x_2 & \frac{x_1^3x_2}{2}& x_1^2x_2^2
\end{pmatrix}.\end{equation*}
\begin{equation*}A(x):=\begin{pmatrix}
1 & 0 & 0& 0& 0\\
0 & 1 & -x_1& \frac{x_1^2}{2}& x_1x_2\\
0 & -x_1& x_1^2 & - \frac{x_1^3}{2} & -x_1^2x_2\\
0 & \frac{x_1^2}{2} & - \frac{x_1^3}{2} & \frac{x_1^4}{4} & \frac{x_1^3x_2}{2} \\
0 & x_1x_2 &-x_1^2x_2 & \frac{x_1^3x_2}{2}& x_1^2x_2^2
\end{pmatrix}.\end{equation*}Then the horizontal gradient and sub-Laplacian are given by:
 \begin{equation*}
\nabla_{\mathcal{B}_5} : = (X_1,X_2), \,\, \text{and } \,\, \mathcal{L}_{\mathcal{B}_5}:= X_1^2 + X_2^2,
\end{equation*}
\begin{equation*}
\nabla_{\mathcal{B}_5} : = (X_1,X_2), \,\, \text{and } \,\, \mathcal{L}_{\mathcal{B}_5}:= X_1^2 + X_2^2,
\end{equation*}where
 \begin{equation*}
X_1:= \partial_{x_1} \,\, \text{and} \,\, X_2:=\partial_{x_2} - x_1 \partial_{x_3} + \frac{x_1^2}{2} \partial_{x_4} + x_1x_2\partial x_5.
\end{equation*}
\begin{equation*}
X_1:= \partial_{x_1} \,\, \text{and} \,\, X_2:=\partial_{x_2} - x_1 \partial_{x_3} + \frac{x_1^2}{2} \partial_{x_4} + x_1x_2\partial x_5.
\end{equation*}Corollary 2.9. Let Ω be a bounded domain in ![]() $\mathcal{B}_5$. Let W(x) and H(x) be positive radially symmetric functions. Then, the inequality
$\mathcal{B}_5$. Let W(x) and H(x) be positive radially symmetric functions. Then, the inequality
 \begin{equation}
\int_{\Omega} W(x) |\nabla_{\mathcal{B}_5} u|^2 dx \geq \int_{\Omega} |\nabla_{\mathcal{B}_5}d|^2H(x) |u|^2 dx,
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\nabla_{\mathcal{B}_5} u|^2 dx \geq \int_{\Omega} |\nabla_{\mathcal{B}_5}d|^2H(x) |u|^2 dx,
\end{equation} holds for all complex-valued functions ![]() $u \in C^1_0(\Omega)$ provided that the following conditions hold:
$u \in C^1_0(\Omega)$ provided that the following conditions hold:
 \begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} s^{Q-1}H(s) ds \lt \infty, \,\, \text{and} \,\, \,\, \phi(r) = 2 \int_{r}^{\infty} s^{Q-1}H(s) ds \lt \infty \,\,\, \text{for} \,\,\, r\geq r_0,
\end{equation} \begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}
\begin{equation}
\int_{r_0}^{\infty} \frac{\phi(s)}{s^{Q-1}W(s)} ds \leq \frac{1}{2} \,\,\, \text{for some} \,\,\, r_0 \gt 0.
\end{equation}3. Rellich inequality with Bessel pairs
We conclude the paper by presenting a Rellich inequality involving Bessel pairs. This result is derived as a byproduct of the second-order Picone type identity in conjunction with the divergence theorem.
Theorem 3.1. Let Ω be a bounded domain in ![]() $\mathbb{R}^n$. Let
$\mathbb{R}^n$. Let ![]() $W \in C^{2}(\Omega)$ and
$W \in C^{2}(\Omega)$ and ![]() $H \in L^1_{loc}(\Omega)$ be positive radially symmetric functions. Suppose that there exists a positive function
$H \in L^1_{loc}(\Omega)$ be positive radially symmetric functions. Suppose that there exists a positive function ![]() $v\in C^{2}(\Omega)$ such that:
$v\in C^{2}(\Omega)$ such that:
with ![]() $-\Delta v \gt 0$ a.e. in Ω. Then for all complex-valued functions
$-\Delta v \gt 0$ a.e. in Ω. Then for all complex-valued functions ![]() $ u \in C^{2}_0(\Omega)$, we have
$ u \in C^{2}_0(\Omega)$, we have
 \begin{equation}
\int_{\Omega} W(x) |\Delta |u||^p dx \geq \int_{\Omega} H(x) |u|^p dx,
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\Delta |u||^p dx \geq \int_{\Omega} H(x) |u|^p dx,
\end{equation} where ![]() $1 \lt p \lt n$.
$1 \lt p \lt n$.
Remark 3.2. Note that the weighted Rellich type inequalities with boundary terms for general (real-valued) vector fields were established by the authors with Suragan in [Reference Ruzhansky, Sabitbek and Suragan26, Reference Ruzhansky, Sabitbek and Suragan30, Reference Ruzhansky, Sabitbek and Suragan32]. Also Goldstein–Kombe–Yerner in [Reference Goldstein, Kombe and Yener19] proved the weighted Rellich inequality in the setting of Carnot groups.
Here we present the corollary for p = 2 to the above theorem:
Corollary 3.3. Let Ω be a bounded domain in ![]() $\mathbb{R}^n$. Let
$\mathbb{R}^n$. Let ![]() $W \in C^{2}(\Omega)$ and
$W \in C^{2}(\Omega)$ and ![]() $H \in L^1_{loc}(\Omega)$ be positive radially symmetric functions. Suppose that a positive function
$H \in L^1_{loc}(\Omega)$ be positive radially symmetric functions. Suppose that a positive function ![]() $v\in C^{\infty}(\Omega)$ satisfies:
$v\in C^{\infty}(\Omega)$ satisfies:
with ![]() $-\Delta v \gt 0$ a.e. in Ω. Then for all complex-valued functions
$-\Delta v \gt 0$ a.e. in Ω. Then for all complex-valued functions ![]() $ u \in C^{2}_0(\Omega)$, we have
$ u \in C^{2}_0(\Omega)$, we have
 \begin{equation}
\int_{\Omega} W(x) |\Delta |u||^2 dx \geq \int_{\Omega} H(x) |u|^2 dx.
\end{equation}
\begin{equation}
\int_{\Omega} W(x) |\Delta |u||^2 dx \geq \int_{\Omega} H(x) |u|^2 dx.
\end{equation}In order to prove Theorem 3.1, we establish the (second-order) Picone type identity.
Lemma 3.4. Let ![]() $\Omega \subset \mathbb{R}^n$ be open set. Let v be twice differentiable a.e. in Ω and satisfying the conditions v > 0 and
$\Omega \subset \mathbb{R}^n$ be open set. Let v be twice differentiable a.e. in Ω and satisfying the conditions v > 0 and ![]() $-\Delta v \gt 0$ a.e. in Ω. Let a complex-valued function u be twice differentiable a.e. in Ω. For p > 1 we define
$-\Delta v \gt 0$ a.e. in Ω. Let a complex-valued function u be twice differentiable a.e. in Ω. For p > 1 we define
 \begin{equation}
R_1(u,v):= |\Delta |u||^p - \Delta\left( \frac{|u|^p}{v^{p-1}} \right) |\Delta v|^{p-2} \Delta v,
\end{equation}
\begin{equation}
R_1(u,v):= |\Delta |u||^p - \Delta\left( \frac{|u|^p}{v^{p-1}} \right) |\Delta v|^{p-2} \Delta v,
\end{equation}and
 \begin{align}
L_1(u,v):= &|\Delta |u||^p - p \left(\frac{|u|}{v}\right)^{p-1} \Delta |u| |\Delta v|^{p-2} \Delta v\\
& + (p-1)\left( \frac{|u|}{v}\right)^p |\Delta v|^p - p(p-1)\frac{|u|^{p-2}}{v^{p-1}} |\Delta v|^{p-2} \Delta v \left( \nabla |u| - \frac{|u|}{v} \nabla v\right)^2. \nonumber
\end{align}
\begin{align}
L_1(u,v):= &|\Delta |u||^p - p \left(\frac{|u|}{v}\right)^{p-1} \Delta |u| |\Delta v|^{p-2} \Delta v\\
& + (p-1)\left( \frac{|u|}{v}\right)^p |\Delta v|^p - p(p-1)\frac{|u|^{p-2}}{v^{p-1}} |\Delta v|^{p-2} \Delta v \left( \nabla |u| - \frac{|u|}{v} \nabla v\right)^2. \nonumber
\end{align}Then, we have
Proof of Lemma 3.4
We show that ![]() $R_1(u,v)=L_1(u,v)$ by a simple expansion of
$R_1(u,v)=L_1(u,v)$ by a simple expansion of ![]() $R_1(u,v)$ as follows:
$R_1(u,v)$ as follows:
 \begin{align*}
\Delta\left( \frac{|u|^p}{v^{p-1}} \right)
& = p \frac{|u|^{p-1}}{v^{p-1}}\Delta |u| - (p-1)\frac{|u|^p}{v^p}\Delta v + p(p-1) \frac{|u|^{p-2}}{v^{p-1}} \left| \nabla |u| - \frac{|u|}{v} \nabla v \right|^2.
\end{align*}
\begin{align*}
\Delta\left( \frac{|u|^p}{v^{p-1}} \right)
& = p \frac{|u|^{p-1}}{v^{p-1}}\Delta |u| - (p-1)\frac{|u|^p}{v^p}\Delta v + p(p-1) \frac{|u|^{p-2}}{v^{p-1}} \left| \nabla |u| - \frac{|u|}{v} \nabla v \right|^2.
\end{align*}The rest of proof is to apply Young’s inequality, then we proceed as follows:
 \begin{equation*}
p \frac{|u|^{p-1}}{v^{p-1}} \Delta |u| |\Delta v|^{p-2} \Delta v \leq |\Delta |u||^p + (p-1) \frac{|u|^p}{v^p}|\Delta v|^p,
\end{equation*}
\begin{equation*}
p \frac{|u|^{p-1}}{v^{p-1}} \Delta |u| |\Delta v|^{p-2} \Delta v \leq |\Delta |u||^p + (p-1) \frac{|u|^p}{v^p}|\Delta v|^p,
\end{equation*}where p > 1. This gives,
 \begin{align*}
L_1(u,v)\geq - p(p-1)\frac{|u|^{p-2}}{v^{p-1}} |\Delta v|^{p-2} \Delta v \left( \nabla |u| - \frac{|u|}{v} \nabla v\right)^2.
\end{align*}
\begin{align*}
L_1(u,v)\geq - p(p-1)\frac{|u|^{p-2}}{v^{p-1}} |\Delta v|^{p-2} \Delta v \left( \nabla |u| - \frac{|u|}{v} \nabla v\right)^2.
\end{align*} It is easy to see that ![]() $L_1(u,v)\geq 0$ by observing the fact
$L_1(u,v)\geq 0$ by observing the fact ![]() $-\Delta v \gt 0$.
$-\Delta v \gt 0$.
Proof of Theorem 3.1
We prove by using the (second-order) Picone type identity and Green’s second identity as follows:
 \begin{align*}
0 \leq \int_{\Omega} W(x) R_1(u,v) dx
&= \int_{\Omega} W(x) |\Delta |u||^p dx -\int_{\Omega} \frac{|u|^p}{v^{p-1}} \Delta (W(x)|\Delta v|^{p-2} \Delta v ) dx\\
& \leq \int_{\Omega} W(x) |\Delta |u||^p dx -\int_{\Omega} H(x) |u|^p dx,
\end{align*}
\begin{align*}
0 \leq \int_{\Omega} W(x) R_1(u,v) dx
&= \int_{\Omega} W(x) |\Delta |u||^p dx -\int_{\Omega} \frac{|u|^p}{v^{p-1}} \Delta (W(x)|\Delta v|^{p-2} \Delta v ) dx\\
& \leq \int_{\Omega} W(x) |\Delta |u||^p dx -\int_{\Omega} H(x) |u|^p dx,
\end{align*}using (3.1). This completes the proof.
3.1. Several versions of Rellich type inequalities
Here by letting ![]() $W\equiv 1$ and
$W\equiv 1$ and  $v=|x|^{-\frac{n-4}{2}}$ into (3.3), we obtain the function:
$v=|x|^{-\frac{n-4}{2}}$ into (3.3), we obtain the function:
 \begin{equation*}
H(x) = \frac{n^2(n-4)^2}{16} |x|^{-4},
\end{equation*}
\begin{equation*}
H(x) = \frac{n^2(n-4)^2}{16} |x|^{-4},
\end{equation*}and inserting to inequality (3.4), we have the following result:
Corollary 3.5. (Rellich inequality)
Let ![]() $n\geq 5$. Then for all complex-valued functions
$n\geq 5$. Then for all complex-valued functions ![]() $u \in C_0^{\infty} (\mathbb{R}^n\backslash\{0\})$, we have
$u \in C_0^{\infty} (\mathbb{R}^n\backslash\{0\})$, we have
 \begin{equation}
\int_{\mathbb{R}^n} |\Delta |u||^2 dx \geq \frac{n^2(n-4)^2}{16} \int_{\mathbb{R}^n} \frac{|u|^2}{|x|^4}dx.
\end{equation}
\begin{equation}
\int_{\mathbb{R}^n} |\Delta |u||^2 dx \geq \frac{n^2(n-4)^2}{16} \int_{\mathbb{R}^n} \frac{|u|^2}{|x|^4}dx.
\end{equation}Corollary 3.6. Let ![]() $n\geq 3$ and
$n\geq 3$ and  $2 - \frac{n}{p} \lt \gamma \lt \frac{n(p-1)}{p}$. Then for all complex-valued functions
$2 - \frac{n}{p} \lt \gamma \lt \frac{n(p-1)}{p}$. Then for all complex-valued functions ![]() $u \in C_0^{\infty} (\mathbb{R}^n\backslash\{0\})$, we have
$u \in C_0^{\infty} (\mathbb{R}^n\backslash\{0\})$, we have
 \begin{equation}
\int_{\mathbb{R}^n} |x|^{\gamma p} |\Delta u|^p dx \geq \left( \frac{n}{p} -2 + \gamma \right)^p \left( \frac{n(p-1)}{p} -\gamma\right)^p \int_{\mathbb{R}^n}|x|^{(\gamma -2)p} |u|^p dx.
\end{equation}
\begin{equation}
\int_{\mathbb{R}^n} |x|^{\gamma p} |\Delta u|^p dx \geq \left( \frac{n}{p} -2 + \gamma \right)^p \left( \frac{n(p-1)}{p} -\gamma\right)^p \int_{\mathbb{R}^n}|x|^{(\gamma -2)p} |u|^p dx.
\end{equation} In the case γ = 0 and for ![]() $1 \lt p \lt n/2$, we get
$1 \lt p \lt n/2$, we get
 \begin{equation}
\int_{\mathbb{R}^n} |\Delta u|^p dx \geq \left( \frac{n}{p} -2 \right)^p \left( \frac{n(p-1)}{p}\right)^p \int_{\mathbb{R}^n}|x|^{-2p} |u|^p dx.
\end{equation}
\begin{equation}
\int_{\mathbb{R}^n} |\Delta u|^p dx \geq \left( \frac{n}{p} -2 \right)^p \left( \frac{n(p-1)}{p}\right)^p \int_{\mathbb{R}^n}|x|^{-2p} |u|^p dx.
\end{equation}Remark 3.7. Note that the weighted Rellich inequality (3.9) is proved by Mitidieri [Reference Mitidieri23] and Lp-Rellich inequality (3.10) by Okazawa [Reference Okazawa24] with the optimal constants, respectively.
Proof of Corollary 3.6
Let us set
where ![]() $\alpha = - (n/p +a -2)$. By inserting to (3.1), we arrive at
$\alpha = - (n/p +a -2)$. By inserting to (3.1), we arrive at
 \begin{align*}
\Delta (W|\Delta v|^{p-2} \Delta v) = C_{\alpha,p,n,\gamma} |x|^{\alpha(p-1) +(\gamma-2)p },
\end{align*}
\begin{align*}
\Delta (W|\Delta v|^{p-2} \Delta v) = C_{\alpha,p,n,\gamma} |x|^{\alpha(p-1) +(\gamma-2)p },
\end{align*}where
 \begin{equation*}C_{\alpha,p,n,\gamma}:=|\alpha|^{p-1} (\alpha + n-2)^{p-1}(\alpha p -\alpha -2p +2 + \gamma p) (\alpha p -\alpha -2p + \gamma p +n).\end{equation*}
\begin{equation*}C_{\alpha,p,n,\gamma}:=|\alpha|^{p-1} (\alpha + n-2)^{p-1}(\alpha p -\alpha -2p +2 + \gamma p) (\alpha p -\alpha -2p + \gamma p +n).\end{equation*}Now we put the value of α in the constant, then we get
 \begin{equation}
H(x) = \left( \frac{n}{p} -2 + \gamma \right)^p \left( \frac{n(p-1)}{p} -\gamma\right)^p |x|^{(\gamma -2)p}.
\end{equation}
\begin{equation}
H(x) = \left( \frac{n}{p} -2 + \gamma \right)^p \left( \frac{n(p-1)}{p} -\gamma\right)^p |x|^{(\gamma -2)p}.
\end{equation}The statement then follows from Theorem 3.1.