Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T01:05:30.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups whose irreducible representations have finite degree II

Published online by Cambridge University Press:  20 January 2009

B. A. F. Wehrfritz
B. A. F. Wehrfritz
Affiliation:
Queen Mary College, Mile End Road, London El 4NS
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If F is a (commutative) field let 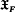denote the class of all groups G such that every irreducible FG-module has finite dimension over F. The introduction to [7] contains motivation for considering these classes 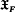and surveys some of the results to date concerning them. In [7] for every field F we determined the finitely generated soluble groups in 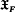. Here, for fields F of characteristic zero, we determine, at least in principle, the soluble groups in 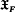. Our main result is the following.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 25 , Issue 3 , October 1982 , pp. 237 - 243
Copyright
Copyright © Edinburgh Mathematical Society 1982

References

REFERENCES

1.Farkas, D. R., Group Rings: an Annotated Questionnaire, Communications in Algebra 8 (1980), 585–602.Google Scholar
2.Jacobson, N., Lectures in Abstract Albegra Vol. 3 (Van Nostrand, New York, 1964).Google Scholar
3.Kegel., O. H. and WEHRFRITZ, B. A. F., Locally Finite Groups (North-Holland Pub. Co., Amsterdam-London, 1973).Google Scholar
4.Kuroš., A. G., The Theory of Groups Vol. 1 (Chelsea Pub. Co., New York, 1956).Google Scholar
5.Passman., D. S., The Algebraic Structure of Group Rings (John Wiley, New York, 1977).Google Scholar
6.Wehrfritz., B.A.F., Infinite Linear Groups (Springer-Verlag, Berlin-Heidelberg-New York, 1973).Google Scholar
7.Wehrfritz., B. A. F., Groups whose irreducible representations have finite degree, Math. Proc. Comb. Soc. 90 (1981), 411–421.Google Scholar