Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T20:55:59.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Groups generated by iterations of polynomials over finite fields

Part of: Finite fields and commutative rings (number-theoretic aspects) Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  05 June 2015

Igor E. Shparlinski
Igor E. Shparlinski*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finite field 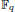of q elements, we consider a trajectory of the map 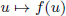associated with a polynomial 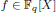]. Using bounds of character sums, under some mild condition on f, we show that for an appropriate constant C > 0 no N ⩾ Cq½ distinct consecutive elements of such a trajectory are contained in a small subgroup 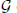of 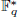, improving the trivial lower bound 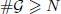. Using a different technique, we also obtain a similar result for very small values of N. These results are multiplicative analogues of several recently obtained bounds on the length of intervals containing N distinct consecutive elements of such a trajectory.

Keywords

finite fieldspolynomial mapssubgroupscharacter sums

MSC classification

Secondary: 11T06: Polynomials 37P05: Polynomial and rational maps
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 59 , Issue 1 , February 2016 , pp. 235 - 245
Copyright
Copyright © Edinburgh Mathematical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Aliev, I. and Smyth, C., Solving algebraic equations in roots of unity, Forum Math. 24 (2012), 641–665.CrossRefGoogle Scholar
2. Beukers, F. and Smyth, C. J., Cyclotomic points on curves, in Number theory for the millennium, II, pp. 67–85 (A. K. Peters/CRC Press, 2002).Google Scholar
3. Bombieri, E., Bourgain, J. and Konyagin, S. V., Roots of polynomials in subgroups of and applications to congruences, Int. Math. Res. Not. 2009 (2009), 1–33.Google Scholar
4. Chang, M.-C., Polynomial iteration in characteristic p, J. Funct. Analysis 263 (2012), 3412–3421.Google Scholar
5. Chang, M.-C., Expansions of quadratic maps in prime fields, Proc. Am. Math. Soc. 142 (2014), 85–92.CrossRefGoogle Scholar
6. Chang, M.-C., Cilleruelo, J., Garaev, M. Z., Hernández, J., Shparlinski, I. E. and Zumalacárregui, A., Points on curves in small boxes and applications, Michigan Math. J. 63 (2014), 503–534.Google Scholar
7. Cilleruelo, J., Garaev, M. Z., Ostafe, A. and Shparlinski, I. E., On the concentration of points of polynomial maps and applications, Math. Z. 272 (2012), 825–837.CrossRefGoogle Scholar
8. Erdős, P. and Murty, R., On the order of a (mod p), in Proc. 5th Canadian Number Theory Association Conf., pp. 87–97 (American Mathematical Society, Providence, RI, 1999).Google Scholar
9. Flajolet, P. and Odlyzko, A. M., Random mapping statistics, in Advances in cryptology: EUROCRYPT '89, Lecture Notes in Computer Science, Volume 434, pp. 329–354 (Springer, 1990).Google Scholar
10. Gao, S., Elements of provable high orders in finite fields, Proc. Am. Math. Soc. 127 (1999), 1615–1623.CrossRefGoogle Scholar
11. Gómez, D., Gutierrez, J., Ibeas, A. and Sevilla, D., Common factors of resultants modulo p , Bull. Austral. Math. Soc. 79 (2009), 299–302.Google Scholar
12. Gutierrez, J. and Shparlinski, I. E., Expansion of orbits of some dynamical systems over finite fields, Bull. Austral. Math. Soc. 82 (2010), 232–239.Google Scholar
13. Iwaniec, H. and Kowalski, E., Analytic number theory (American Mathematical Society, Providence, RI, 2004).Google Scholar
14. Konyagin, S. V. and Shparlinski, I. E., Character sums with exponential functions and their applications (Cambridge University Press, 1999).Google Scholar
15. Leroux, L., Computing the torsion points of a variety defined by lacunary polynomials, Math. Comp. 81 (2012), 1587–1607.CrossRefGoogle Scholar
16. Niederreiter, H. and Winterhof, A., Multiplicative character sums of nonlinear recurring sequences, Acta Arith. 111 (2004), 299–305.CrossRefGoogle Scholar
17. Zannier, U., Lecture notes on Diophantine analysis, Publications of the Scuola Normale Superiore, Volume 8 (Edizioni Della Normale, Pisa, 2009).Google Scholar