Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T23:03:34.974Z Has data issue: false hasContentIssue false
  • English
  • Français

The Group of Automorphisms of the Algebra of one-Sided Inverses of a Polynomial Algebra. II

Published online by Cambridge University Press:  03 June 2015

V. V. Bavula
V. V. Bavula*
Affiliation:
Department of Pure Mathematics, University of Sheffield, Hicks Building, Sheffield S3 7RH, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The algebra 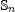of one-sided inverses of a polynomial algebra Pn in n variables is obtained from Pn by adding commuting left (but not two-sided) inverses of the canonical generators of the algebra Pn. The algebra 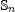is isomorphic to the algebra

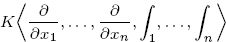
of scalar integro-differential operators provided that char(K) = 0. Ignoring the non-Noetherian property, the algebra 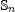belongs to a family of algebras like the nth Weyl algebra An and the polynomial algebra P2n. Explicit generators are found for the group Gn of automorphisms of the algebra 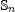and for the group 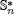of units of 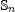(both groups are huge). An analogue of the Jacobian homomorphism AutK-alg (Pn) → K* is introduced for the group Gn (notice that the algebra 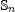is non-commutative and neither left nor right Noetherian). The polynomial Jacobian homomorphism is unique. Its analogue is also unique for n > 2 but for n = 1, 2 there are exactly two of them. The proof is based on the following theorem that is proved in the paper:

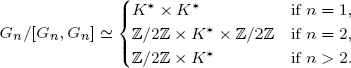
Keywords

group of automorphismsgroup generatorsinner automorphismsFredholm operatorsindex of an operatorsemi-direct and exact products of groupsPrimary 16W2014E0714H3714R1014R15
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 3 , October 2015 , pp. 543 - 580
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bass, H., Algebraic K-theory (W. A. Benjamin, New York, 1968).Google Scholar
2.Bavula, V. V., The Jacobian algebras, J. Pure Appl. Alg. 213 (2009), 664–685.Google Scholar
3.Bavula, V. V., The group of automorphisms of the first Weyl algebra in prime characteristic and the restriction map, Glasgow Math. J. 5 (2009), 263–274.Google Scholar
4.Bavula, V. V., The algebra of one-sided inverses of a polynomial algebra, J. Pure Appl. Alg. 214 (2010), 1874–1897.CrossRefGoogle Scholar
5.Bavula, V. V., K1 and the group of automorphisms of the algebra of one-sided inverses of a polynomial algebra in two variables, J. K-theory Applic. Algebra Geom. Analysis Topolog. 10(3 (2012), 583–601.Google Scholar
6.Bavula, V. V., The group of automorphisms of the Jacobian algebra , J. Pure Appl. Alg. 216 (2012) 535–564.Google Scholar
7.Bavula, V. V., The group of automorphisms of the algebra of one-sided inverses of a polynomial algebra, Muenster J. Math. 6 (2013), 1–51.Google Scholar
8.Dixmier, J., Sur les algèbres de Weyl, Bull. Soc. Math. France 96 (1968), 209–242.CrossRefGoogle Scholar
9.Fulton, W., Intersection theory (Springer, 1984).Google Scholar
10.Jacobson, N., Structure of rings, revised edn, American Mathematical Society Collo quium Publications, Volume 37 (American Mathematical Society, Providence, RI, 1968).Google Scholar
11.Jung, H. W. E., Über ganze birationale Transformationen der Ebene, J. Reine Angew. Math. 184 (1942), 161–174.Google Scholar
12.Makar-Limanov, L., On automorphisms of Weyl algebra, Bull. Soc. Math. France 112 (1984), 359–363.Google Scholar
13.Milnor, J., Introduction to algebraic K-theory, Annals of Mathematics Studies, Volume 72 (Princeton University Press, Princeton, NJ, 1971).Google Scholar
14.Swan, R. G., Algebraic K-theory, Lecture Notes in Mathematics, Volume 76 (Springer, 1968).Google Scholar
15.Van der Kulk, W., On polynomial rings in two variables, Nieuw Arch. Wisk. 1(3 (1953), 33–41.Google Scholar