Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T18:33:54.318Z Has data issue: false hasContentIssue false
  • English
  • Français

The graded Cartan matrix and global dimension of 0-relations algebras

Published online by Cambridge University Press:  20 January 2009

W. D. Burgess
W. D. Burgess
Affiliation:
Department of Mathematics, University of Ottawa, Ottawa, Canada, K1N 6N5
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Cartan matrix C of a left artinian ring A, with indecomposable projectives P1,…,Pn and corresponding simples Si=Pi/JPi, is an n×n integral matrix with entries Cij, the number of copies of the simple sj which appear as composition factors of Pi. A relationship between the invertibility of this matrix (as an integral matrix) and the finiteness of the global dimension has long been known: gl dim A < ∞⇒det C = ± 1 (Eilenberg [3]). More recently Zacharia [9] has shown that gl dim A ≦ 2⇒det C = 1, and in fact no rings of finite global dimension are known with det C = −1. The converse, det C = l⇒gl dim A < ∞, is false, as easy examples show ([[1) or [3]). However if A is left serial, gl dim A < ∞iff det C = l [1]. If A = ⊕n ≧ 0 An is ℤ-graded and the radical J = ⊕n ≧ 0 An, Wilson [8] calls such rings positively graded. Here there is a graded Cartan matrix 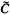with entries from ℤ[X] and gl dim A < ∞⇒det 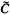= 1 and, hence, det C = l [8, Prop. 2.2].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 3 , October 1987 , pp. 351 - 362
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Burgess, W. D., Fuller, K. R., Voss, E. and Zimmermann-Huisgen, B., The Cartan matrix as an indicator of finite global dimension for artinian rings, Proc. Amer. Math. Soc. 95 (1985),157–165.CrossRefGoogle Scholar
2.Cohn, P. M., Free Rings and their Relations (Academic Press, London and New York, 1971).Google Scholar
3.Eilenberg, S., Algebras of cohomologically finite dimension, Comment. Math. Helv. 28 (1954), 310–319.CrossRefGoogle Scholar
4.Fossum, R., Griffith, P. and Reiten, I., Trivial extensions of abelian categories and applications to rings: an expository account, in Ring Theory (Ed. Gordon, R.) (Academic Press, New York, London, 1972).Google Scholar
5.Gabriel, P., Unzerlegbare Darstellungen I, Manuscripta Math. 6 (1972), 71–103.CrossRefGoogle Scholar
6.Green, E. L., Graphs with relations, coverings and group-graded algebras, Trans. Amer. Math. Soc. 279 (1983), 297–310.CrossRefGoogle Scholar
7.Green, E. L., Happel, D. and Zacharia, D., Projective resolutions over artin algebras with zero relations, Illinois J. Math. 29 (1985), 180–190.CrossRefGoogle Scholar
8.Wilson, G. V., The Cartan map on categories of graded modules, J. Algebra 85 (1983), 390–398.CrossRefGoogle Scholar
9.Zacharia, D., On the Cartan matrix of an artin algebra of global dimension two, J. Algebra 82 (1983), 353–357.CrossRefGoogle Scholar