No CrossRef data available.
Article contents
Geometrical Theory of the Hyperbolic Functions
Published online by Cambridge University Press: 20 January 2009
Extract
1. If PQRS be an Hyperbola, OE, OF its asymptotes, P, Q, R, S any points on it such that the sectorial area OPQ = sectorial area ORS; and if PA, QB, RC, SD be ordinates to one asymptote and parallel to the other, it is known that
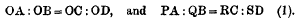
Hence if A, B, C … be taken so that OA, OB, OC … are in continued proportion, the areas OPQ, OQR, ORS … are all equal, and since the number of points can be made as large as we please, the sum of the sectorial areas can be made as large as we please. ∴ The area between an asymptote, the curve, and any radius vector is infinite.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1898


