Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:10:17.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometrical Interpretation of a few concomitants of the cubic in the Argand Plane

Published online by Cambridge University Press:  20 January 2009

W. Saddler
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

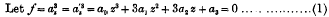
be the binary cubic whose coefficients a1, are complex numbers represented on the Argand Plane. Then if its roots are z1, z2, z3, the three corresponding points form the vertices of a triangle A1 A2 A3. Let this triad of points be said to represent the cubic. Then its Hessian

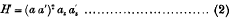
is represented by a certain pair of other points; likewise every first polar

associates a definite pair of points (z) with any given point (y).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 42 , February 1923 , pp. 41 - 45
Copyright
Copyright © Edinburgh Mathematical Society 1923

References

* Cf. Grace and Young, Algtbra of Invariants (190) p.

* See Grace and Young, loc. cit., pp. 209, 211.

* Cf. Graoe and Young, loc. cit.