Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-22T20:40:56.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data

Part of: Representations of solutions Partial differential equations Parabolic equations and systems Miscellaneous topics - Partial differential equations Harmonic analysis in several variables Special classes of linear operators

Published online by Cambridge University Press:  10 December 2014

Vagif S. Guliyev  and
Lubomira G. Softova
Vagif S. Guliyev
Affiliation:
Department of Mathematics, Ahi Evran University, Kirsehir, Turkey Institute of Mathematics and Mechanics, National Academy of Sciences of Azerbaijan, Baku, Azerbaijan, ([email protected])
Lubomira G. Softova
Affiliation:
Department of Civil Engineering, Design, Construction Industry and Environment, Second University of Naples, Via Roma 29, Aversa (CE) 81031, Italy, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

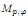We prove continuity in generalized parabolic Morrey spaces of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global -regularity result for the Cauchy—Dirichlet problem for linear uniformly parabolic equations with vanishing mean oscillation (VMO) coefficients.

Keywords

generalized Morrey spacessublinear operatorsCalderón—Zygmund integralsBMOVMOCauchy—Dirichlet problem

MSC classification

Primary: 35K20: Initial-boundary value problems for second-order parabolic equations
Secondary: 35B45: A priori estimates 35D35: Strong solutions 35R05: Partial differential equations with discontinuous coefficients or data 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.) 47B38: Operators on function spaces (general)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 1 , February 2015 , pp. 199 - 218
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Acquistapace, P., On BMO regularity for linear elliptic systems, Annali Mat. Pura Appi. 161 (1992), 231–270.Google Scholar
2.Akbulut, A., Guliyev, V. S. and Mustafayev, R., On the boundedness of the maximal operator and singular integral operators in generalized Morrey spaces, Math. Bohem. 137(1) (2012), 27–43.Google Scholar
3.Bramanti, M. and Cerutti, M. C., solvability for the Cauchy–Dirichlet problem for parabolic equations with VMO coefficients, Commun. PDEs 18 (1993), 1735–1763.Google Scholar
4.Carro, M., Pick, L., Soria, J. and Stepanov, V. D., On embeddings between classical Lorentz spaces, Math. Inequal. App1. 4(3) (2001), 397–428.Google Scholar
5.Chiarenza, F. and Frasca, M., Morrey spaces and Hardy–Littlewood maximal function, Rend. Mat. 7 (1987), 273–279.Google Scholar
6.Chiarenza, F., Frasca, M. and Longo, M. P., Interior -estimates for nondivergence elliptic equations with discontinuous coefficients, Ric. Mat. 40 (1991), 149–168.Google Scholar
7.Fabes, E. B. and Rivière, N., Singular integrals with mixed homogeneity, Studia Math. 27 (1996), 19–38.CrossRefGoogle Scholar
8.Guliyev, V. S., Integral operators on function spaces on the homogeneous groups and on domains in ℝn, PhD Thesis, Steklov Institute of Mathematics (1994; in Russian).Google Scholar
9.Guliyev, V. S., Boundedness of the maximal, potential and singular operators in the generalized Morrey spaces, J. Inequal. Applicat. 2009 (2009), 503948.Google Scholar
10.Guliyev, V. S. and Mushtagov, F. M., Parabolic equations with VMO coefficients in weighted Lebesgue spaces, Proc. Razmadze Math. Inst. 137 (2005), 1–27.Google Scholar
11.Guliyev, V. S. and Softova, L. G., Global regularity in generalized Morrey spaces of solutions to non-divergence elliptic equations with VMO coefficients, Potent. Analysis 38(3) (2013), 843–862.Google Scholar
12.Guliyev, V. S., Aliyev, S. S., Karaman, T. and Shukurov, P., Boundedness of sublinear operators and commutators on generalized Morrey spaces, Integ. Eqns Operat. Theory 71(3) (2011), 327–355.Google Scholar
13.John, F. and Nirenberg, L., On functions of bounded mean oscillation, Commun. Pure Appl. Math. 14 (1961), 415–426.Google Scholar
14.Jones, P. W., Extension theorems for BMO, Indiana Univ. Math. J. 29 (1980), 41–66.Google Scholar
15.Ladyzhenskaya, O. A., Solonnikov, V. A. and Ural′tseva, N. N., Linear and quasilinear equations of parabolic type, Translations of Mathematical Monographs, Volume 23 (American Mathematical Society, Providence, RI, 1968).Google Scholar
16.Mizuhara, T., Boundedness of some classical operators on generalized Morrey spaces, in ICM-90 Satellite Conference Proceedings: Harmonic Analysis, pp. 183–189 (Springer, 1991).CrossRefGoogle Scholar
17.Morrey, C. B., On the solutions of quasi-linear elliptic partial differential equations, Trans. Am. Math. Soc. 43 (1938), 126–166.Google Scholar
18.Nakai, E., Hardy-Littlewood maximal operator, singular integral operators and the Riesz potentials on generalized Morrey spaces, Math. Nachr. 166 (1994), 95–103.Google Scholar
19.Nakai, E., The Campanato, Morrey and Hölder spaces on spaces of homogeneous type, Studia Math. 176(1) (2006), 1–19.Google Scholar
20.Palagachev, D. K. and Softova, L. G., Singular integral operators, Morrey spaces and fine regularity of solutions to PDEs, Potent. Analysis 20 (2004), 237–263.CrossRefGoogle Scholar
21.Palagachev, D. K., Ragusa, M. A. and Softova, L. G., Cauchy-Dirichlet problem in Morrey spaces for parabolic equations with discontinuous coefficients, Boll. UMI B8(6) (2003), 667–683.Google Scholar
22.Sarason, D., On functions of vanishing mean oscillation, Trans. Am. Math. Soc. 207 (1975), 391–405.CrossRefGoogle Scholar
23.Softova, L. G., Singular integrals and commutators in generalized Morrey spaces, Acta Math. Sinica 22 (2006), 757–766.CrossRefGoogle Scholar
24.Softova, L. G., Singular integral operators in Morrey spaces and interior regularity of solutions to systems of linear PDEs, J. Global Optim. 40 (2008), 427–442.CrossRefGoogle Scholar
25.Softova, L. G., Morrey-type regularity of solutions to parabolic problems with discontinuous data, Manuscr. Math. 136(3) (2011), 365–382.CrossRefGoogle Scholar
26.Softova, L. G., The Dirichlet problem for elliptic equations with VMO coefficients in generalized Morrey spaces, in Advances in harmonic analysis and operator theory, the Stefan Samko anniversary volume, Operator Theory: Advances and Applications, Volume 229, pp. 371–386 (Springer, 2013).Google Scholar
27.Softova, L. G., Parabolic oblique derivative problem with discontinuous coefficients in generalized Morrey spaces, Ric. Mat. 62(2) (2013), 265–278.Google Scholar
28.Stein, E., Harmonic analysis: real-variable methods, orthogonality and oscillatory integrals, Princeton Mathematical Series, Volume 43 (Princeton University Press, 1993).Google Scholar