No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
The methods now adopted in the teaching of elementary geometry have made it most important that the teacher should have clear views upon the nature of the problems which are soluble by Euclid's methods: that is, with the aid of the ruler and compass only. With this general question I have dealt in another place. In this paper I give a short account of the argument by means of which Gauss proved that the only regular polygons of n sides, which can be constructed by Euclid's methods, are those in which n, when broken up into prime factors, takes the form
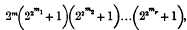
m1, m2, m3,…mr being all different.
page 121 note † Cf.Math. Gazette, VoL V., No. 83, p. 170 (1910).Google Scholar
page 121 note † Gauss: Werke, Bd. I. Disquisitiones arithmeticae, §365.
page 121 note ‡ Enriques, : Questioni riguardanti la Geometria Elementare (Bologna 1900).Google ScholarGerman Translation, Fragen der Elementargeometrie (Leipzig, 1908–1910).Google Scholar
page 121 note § Klein, : Vorträge über ausgewählte Fragen der Elementargeometrie (Leipzig, 1895).Google Scholar
page 121 note ║ This translation by W. W. Beman and D. E. Smith is entitled Famous Problems in Elementary Geometry, and was published by Ginn & Co. in 1897.
page 122 note * Cf. Hardy's, Pure Mathematics (pp. 64–65), or the paper by the author already referred to.Google Scholar
page 122 note † Cf. Enriques: loc. cit. Article XI, §3.
Petersen : Théorie des équations algébriques, §91
page 123 note * Cf. Enriques: loc. cit. Article XI, §5.
Klein : loc. cit. Chapter III., §§6, 7.
The proof usually given is that of Eisenstein, : Crelle's Journal, Bd. XXXIX., p. 167.Google Scholar
page 123 note † Weber-Wellstein, : Encyklopädie der Elementar-Malthematik, Bd. I., §78;Google Scholar or, Bachmann, , Die Lehre von der Kreistheilung, p. 28 (Leipzig, 1872).Google Scholar
page 125 note * Cf. Enriques : loc. cit. Article XI, §7.
page 126 note * Cf. Enriques: loc. cit. Article XI, §10.
Bachmann: loc. cit. p. 32.
page 128 note * Cf. C. Smith's Algebra, ch. XXIX., §399.
You have
Access