Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-10T12:11:41.396Z Has data issue: false hasContentIssue false
  • English
  • Français

A. G. D. Watson's principal directions for a Riemannian V4

Published online by Cambridge University Press:  20 January 2009

H. S. Ruse
H. S. Ruse
Affiliation:
University College, Southampton.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A. G. D. Watson (1939-41), remarking that there are no Ricci principal directions ata world-point of space-time at which the Einstein equations 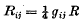are satisfied, shows how to define at any world-point a set of principal directions intrinsically related to the Riemann tensor Rijkl itself. These directions are unique except when the space-time has any kind of rotational symmetry about the world-point.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 7 , Issue 3 , February 1946 , pp. 144 - 152
Copyright
Copyright © Edinburgh Mathematical Society 1946

References

REFERENCES

Churchill, R. V., 1932. “On the geometry of the Riemann tensor,” Trans. Amer. Math. Soc., vol. 34, pp. 126–152.CrossRefGoogle Scholar
Eisenhart, L. P., 1926. Biemannian geometry, Princeton.Google Scholar
Ruse, H. S., 1944. “On the line-geomefcry of the Riemann tensor,” Proc. Roy. Soc., Edinburgh, vol. 62, pp. 64–73.Google Scholar
Ruse, H. S., 1947 (?). “The self-polar Riemann complex for a V 4,” Proc. London Math. Soc. In press.Google Scholar
Struik, D. J., 1927–1928. “On sets of principal directions in a Riemannian manifold of four dimensions,” Journ. Math. Phys., Mass. Inst. Tech., vol. 7, pp. 193–197.Google Scholar
Watson, A. G. D., 1939–1941. “Principal directions in a gravitational field,” Proc. Edinburgh Math. Soc. (2), vol. 6, pp. 12–16.CrossRefGoogle Scholar