Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T00:37:46.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Free non-associative principal train algebras

Published online by Cambridge University Press:  20 January 2009

P. Holgate
P. Holgate
Affiliation:
Birkbeck CollegeLondon Wcie 7HX
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The definitions of finite dimensional baric, train, and special train algebras, and of genetic algebras in the senses of Schafer and Gonshor (which coincide when the ground field is algebraically closed, and which I call special triangular) are given in Worz-Busekros's monograph [8]. In [6] I introduced applications requiring infinite dimensional generalisations. The elements of these algebras were infinite linear forms 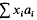in basis elements a0, a1,… and complex coefficients such that 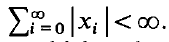In this paper I consider only algebras whose elements are forms 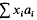which only a finite number of the xi are non zero.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 3 , October 1984 , pp. 313 - 319
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

REFERENCES

1.Abraham, V. M.A note on train algebras, Proc. Edinburgh Math. Soc.. (2) 20 (1976), 53–58.Google Scholar
2.Abraham, V. M.Linearising quadratic transformations in genetic algebras, Proc. London Math. Soc. (3) 40 (1980), 346–363.Google Scholar
The induced linear transformation in a genetic algebra, Proc. London Math. Soc. (3) 40 (1980) 364–384.Google Scholar
3.Holgate, P.Sequences of powers in genetic algebras, J. London Math. Soc. 42 (1967), 489–496.CrossRefGoogle Scholar
4.Holgate, P., Selfing in genetic algebras, J. Math. Biol. 6 (1978), 197–206.Google Scholar
5.Holgate, P., Genetic algebras for some inbreeding systems, Proc. Royal Soc. Edinburgh A 86 (1980), 65–74.Google Scholar
6.Holgate, P.Population algebras, J. Royal Statist. Soc. B43 (1981), 1–19.Google Scholar
7.Mchale, D. and Ringwood, G. A.Haldane linearisation of baric algebras, J. London Math. Soc. (2) 28 (1983), 17–26.Google Scholar
8.Wörz-Busekros, A.Algebras in genetics (Lectures Notes in Biomathematics 36, Springer Verlag, 1980).Google Scholar