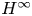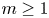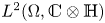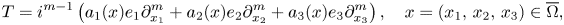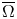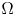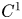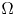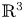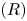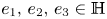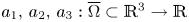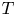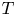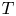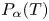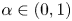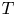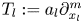1. Introduction
Using the $S$![]() -functional calculus, in the series of papers [Reference Colombo and Gantner15, Reference Colombo, Mongodi, Peloso and Pinton21–Reference Colombo, Deniz-Gonzales and Pinton24], we defined the fractional powers of a class of vector operators with non-constant coefficients. In this paper, we consider the quaternionic differential operators of the form
-functional calculus, in the series of papers [Reference Colombo and Gantner15, Reference Colombo, Mongodi, Peloso and Pinton21–Reference Colombo, Deniz-Gonzales and Pinton24], we defined the fractional powers of a class of vector operators with non-constant coefficients. In this paper, we consider the quaternionic differential operators of the form
and we prove that under suitable conditions on the coefficients, it admits well-defined fractional powers. In order to state our results, we give some details on the quaternion techniques based on the spectral theory on the $S$![]() -spectrum. For a complete introduction of the $S$
-spectrum. For a complete introduction of the $S$![]() -functional calculus see the books [Reference Colombo and Gantner16], [Reference Colombo, Gantner and Kimsey20], here we briefly introduce the main aspects of this theory.
-functional calculus see the books [Reference Colombo and Gantner16], [Reference Colombo, Gantner and Kimsey20], here we briefly introduce the main aspects of this theory.
1.1. The $S$ -functional calculus
-functional calculus
An element in the quaternions $\mathbb {H}$![]() is of the form $s=s_0+s_1e_1+s_2e_2+s_3e_3$
is of the form $s=s_0+s_1e_1+s_2e_2+s_3e_3$![]() , where $s_0$
, where $s_0$![]() , $s_\ell$
, $s_\ell$![]() are real numbers ($\ell =1,2,3$
are real numbers ($\ell =1,2,3$![]() ), ${\rm Re}(s):=s_0$
), ${\rm Re}(s):=s_0$![]() denotes the real part of $s$
denotes the real part of $s$![]() and $e_\ell$
and $e_\ell$![]() , for $\ell =1,2,3$
, for $\ell =1,2,3$![]() , are the imaginary units which satisfy the relations: $e_1^{2}=e_2^{2}=e_3^{2}=e_1e_2e_3=-1$
, are the imaginary units which satisfy the relations: $e_1^{2}=e_2^{2}=e_3^{2}=e_1e_2e_3=-1$![]() . The modulus of $s$
. The modulus of $s$![]() is defined as $|s|=(s_0^{2}+s_1^{2}+s_2^{2}+s_3^{2})^{1/2}$
is defined as $|s|=(s_0^{2}+s_1^{2}+s_2^{2}+s_3^{2})^{1/2}$![]() and the conjugate is given by $\overline {s}=s_0-s_1e_1-s_2e_2-s_3e_3$
and the conjugate is given by $\overline {s}=s_0-s_1e_1-s_2e_2-s_3e_3$![]() . In the sequel, we will denote by $\mathbb {S}$
. In the sequel, we will denote by $\mathbb {S}$![]() the unit sphere of purely imaginary quaternions, an element $j$
the unit sphere of purely imaginary quaternions, an element $j$![]() in $\mathbb {S}$
in $\mathbb {S}$![]() is such that $j^{2}=-1$
is such that $j^{2}=-1$![]() . We consider a two-sided quaternionic Banach space $V$
. We consider a two-sided quaternionic Banach space $V$![]() and we denote the set of closed densely defined quaternionic right linear operators on $V$
and we denote the set of closed densely defined quaternionic right linear operators on $V$![]() by $\mathcal {K}(V)$
by $\mathcal {K}(V)$![]() . The Banach space of all bounded right linear operators on $V$
. The Banach space of all bounded right linear operators on $V$![]() is indicated by the symbol $\mathcal {B}(V)$
is indicated by the symbol $\mathcal {B}(V)$![]() and is endowed with the natural operator norm. For $T\in \mathcal {K}(V)$
and is endowed with the natural operator norm. For $T\in \mathcal {K}(V)$![]() , we define the operator associated with the $S$
, we define the operator associated with the $S$![]() -spectrum as:
-spectrum as:
where $\mathcal {Q}_{s}(T):\mathcal {D}(T^{2})\to V$![]() , where $\mathcal {D}(T^{2})$
, where $\mathcal {D}(T^{2})$![]() is the domain of $T^{2}$
is the domain of $T^{2}$![]() . We define the $S$
. We define the $S$![]() -resolvent set of $T$
-resolvent set of $T$![]() as
as
and the $S$![]() -spectrum of $T$
-spectrum of $T$![]() as
as
The operator $\mathcal {Q}_{s}(T)^{-1}$![]() is called the pseudo $S$
is called the pseudo $S$![]() -resolvent operator. For $s\in \rho _S(T)$
-resolvent operator. For $s\in \rho _S(T)$![]() , the left $S$
, the left $S$![]() -resolvent operator is defined as
-resolvent operator is defined as
and the right $S$![]() -resolvent operator is given by
-resolvent operator is given by
The fractional powers of an operator $T$![]() such that $j\mathbb {R}\subset \rho _S(T)$
such that $j\mathbb {R}\subset \rho _S(T)$![]() for any $j\in \mathbb {S}$
for any $j\in \mathbb {S}$![]() , are denoted by $P_{\alpha }(T)$
, are denoted by $P_{\alpha }(T)$![]() and are defined as follows. For any $j\in \mathbb {S}$
and are defined as follows. For any $j\in \mathbb {S}$![]() , for $\alpha \in (0,1)$
, for $\alpha \in (0,1)$![]() and $v\in \mathcal {D}(T)$
and $v\in \mathcal {D}(T)$![]() , we set
, we set
or
where $ds_j=ds/j$![]() . These formulas are a consequence of the quaternionic version of the $H^{\infty }$
. These formulas are a consequence of the quaternionic version of the $H^{\infty }$![]() -functional calculus based on the $S$
-functional calculus based on the $S$![]() -spectrum, again see [Reference Colombo and Gantner16] for details. For the generation of the fractional powers $P_{\alpha }(T)$
-spectrum, again see [Reference Colombo and Gantner16] for details. For the generation of the fractional powers $P_{\alpha }(T)$![]() , a crucial assumption on the $S$
, a crucial assumption on the $S$![]() -resolvent operators is that, for $s\in \mathbb {H}\setminus \{0\}$
-resolvent operators is that, for $s\in \mathbb {H}\setminus \{0\}$![]() with ${\rm Re}(s)=0$
with ${\rm Re}(s)=0$![]() , the estimates
, the estimates
hold with a constant $\Theta >0$![]() that does not depend on $s$
that does not depend on $s$![]() . It is important to observe that the conditions (1.6) assure that the integrals (1.4) and (1.5) are convergent and so the fractional powers are well defined.
. It is important to observe that the conditions (1.6) assure that the integrals (1.4) and (1.5) are convergent and so the fractional powers are well defined.
For the definition of the fractional powers of the operator $T$![]() , we can use equivalently the integral representation in (1.4) or the one in (1.5). Moreover, they correspond to a modified version of Balakrishnan's formula that takes only spectral points with positive real part into account.
, we can use equivalently the integral representation in (1.4) or the one in (1.5). Moreover, they correspond to a modified version of Balakrishnan's formula that takes only spectral points with positive real part into account.
Remark 1.1 It is clear from the definition of the $S$![]() -resolvent operators that to use the $S$
-resolvent operators that to use the $S$![]() -functional calculus for the definition of the fractional powers of an operator $T$
-functional calculus for the definition of the fractional powers of an operator $T$![]() we have to determine if $\mathcal {Q}_s(T)$
we have to determine if $\mathcal {Q}_s(T)$![]() is invertible for any $s\in \mathbb {H}$
is invertible for any $s\in \mathbb {H}$![]() such that $s\neq 0$
such that $s\neq 0$![]() and $\mathrm {Re}(s)=0$
and $\mathrm {Re}(s)=0$![]() , and, moreover, if estimates of the type (1.6) hold, see Problem 1.4.
, and, moreover, if estimates of the type (1.6) hold, see Problem 1.4.
1.2. Operators of order one vs operators of order $m>1$
In some of our previous papers, we have defined fractional powers of operators of first order such as

acting on functions $u:\Omega \subset \mathbb {R}^{3}\to \mathbb {R}$![]() belonging to $H^{1}_0(\Omega,\mathbb {R})\subset L^{2}(\Omega,\mathbb {R})$
belonging to $H^{1}_0(\Omega,\mathbb {R})\subset L^{2}(\Omega,\mathbb {R})$![]() where $\Omega$
where $\Omega$![]() is a (possibly) unbounded domain with $C^{1}$
is a (possibly) unbounded domain with $C^{1}$![]() boundary. To use the $S$
boundary. To use the $S$![]() -functional calculus, first we identify the gradient operator with the quaternionic gradient operator
-functional calculus, first we identify the gradient operator with the quaternionic gradient operator

and we consider the operator $\mathcal {Q}_{s}(T)$![]() defined in a weak sense over $H^{1}_0(\Omega,\mathbb {H})\subset L^{2}(\Omega, \mathbb {H})$
defined in a weak sense over $H^{1}_0(\Omega,\mathbb {H})\subset L^{2}(\Omega, \mathbb {H})$![]() . It is important to observe that the above identification has some consequence on the bilinear form $b_s(u,v)=\langle \mathcal {Q}_s(T)(u), v\rangle _\mathbb {H}$
. It is important to observe that the above identification has some consequence on the bilinear form $b_s(u,v)=\langle \mathcal {Q}_s(T)(u), v\rangle _\mathbb {H}$![]() , where $\langle a,b \rangle _\mathbb {H}:=\overline a b$
, where $\langle a,b \rangle _\mathbb {H}:=\overline a b$![]() for all $a,\, b\in \mathbb {H}$
for all $a,\, b\in \mathbb {H}$![]() . Indeed, performing an integration by parts, we have (see in the following):
. Indeed, performing an integration by parts, we have (see in the following):

where the “other terms” are the scalar products of the first derivatives of $u$![]() with $u$
with $u$![]() multiplied by the derivative of the coefficients. In the formula, we indicate that $b_s(u,u)$
multiplied by the derivative of the coefficients. In the formula, we indicate that $b_s(u,u)$![]() contains two positive terms: the $L^{2}$
contains two positive terms: the $L^{2}$![]() -norm of $u$
-norm of $u$![]() and the $L^{2}$
and the $L^{2}$![]() -norm of the first derivative of $u$
-norm of the first derivative of $u$![]() multiplied by the coefficients $a_j$
multiplied by the coefficients $a_j$![]() 's. This fact allows us to determine some conditions on the coefficients $a_j$
's. This fact allows us to determine some conditions on the coefficients $a_j$![]() 's in order to guarantee the continuity and the coercivity of $b_s(\cdot,\cdot )$
's in order to guarantee the continuity and the coercivity of $b_s(\cdot,\cdot )$![]() and, moreover, the uniform estimates for the $S$
and, moreover, the uniform estimates for the $S$![]() -resolvent operator.
-resolvent operator.
In this paper, we consider vector operators of order $m>1$![]() and $m\in \mathbb {N}$
and $m\in \mathbb {N}$![]() of the type
of the type

If we consider the previous identification
and we consider the operator $\mathcal {Q}_s(T)$![]() defined in a weak sense over $H^{m}_0(\Omega,\mathbb {H})\subset L^{2}(\Omega, \mathbb {H})$
defined in a weak sense over $H^{m}_0(\Omega,\mathbb {H})\subset L^{2}(\Omega, \mathbb {H})$![]() , we have to distinguish the cases of $m$
, we have to distinguish the cases of $m$![]() odd or even. If $m$
odd or even. If $m$![]() is odd using $m$
is odd using $m$![]() -times an argument of integration by parts we obtain
-times an argument of integration by parts we obtain

and the bilinear form still contains two positive terms: the $L^{2}$![]() -norm of $u$
-norm of $u$![]() and the $L^{2}$
and the $L^{2}$![]() -norm of the derivatives of order $m$
-norm of the derivatives of order $m$![]() . If we try to compute the bilinear form in the same way when $m$
. If we try to compute the bilinear form in the same way when $m$![]() is even, we obtain
is even, we obtain

losing the positivity of the first term. One way to overcome this problem is to identify $T$![]() with
with
if $m$![]() is odd and with
is odd and with
if $m$![]() is even where $i$
is even where $i$![]() is the imaginary unit of $\mathbb {C}$
is the imaginary unit of $\mathbb {C}$![]() . In other words, we have complexified the coefficients of the quaternionic gradient operator and the operator $T$
. In other words, we have complexified the coefficients of the quaternionic gradient operator and the operator $T$![]() is identified with the quaternionic gradient operator with real coefficients if $m$
is identified with the quaternionic gradient operator with real coefficients if $m$![]() is odd or with the quaternionic gradient operator with purely imaginary coefficients if $m$
is odd or with the quaternionic gradient operator with purely imaginary coefficients if $m$![]() is even. For the precise definitions of $b_s(\cdot,\cdot )$
is even. For the precise definitions of $b_s(\cdot,\cdot )$![]() and of the quaternionic Hilbert space $\mathbb {C}\otimes \mathbb {H}$
and of the quaternionic Hilbert space $\mathbb {C}\otimes \mathbb {H}$![]() , see § 2. In light of these considerations, we give the following definition.
, see § 2. In light of these considerations, we give the following definition.
Definition 1.2 Let $\Omega$![]() be a $C^{1}$
be a $C^{1}$![]() -domain in $\mathbb {R}^{3}$
-domain in $\mathbb {R}^{3}$![]() , bounded or unbounded, and let $a_l: \overline \Omega \to \mathbb {R}$
, bounded or unbounded, and let $a_l: \overline \Omega \to \mathbb {R}$![]() for $l=1,\, 2,\, 3$
for $l=1,\, 2,\, 3$![]() be $C^{m}(\overline \Omega )$
be $C^{m}(\overline \Omega )$![]() functions. We define in a classical way over $C^{m}(\overline \Omega, \mathbb {C}\otimes \mathbb {H})$
functions. We define in a classical way over $C^{m}(\overline \Omega, \mathbb {C}\otimes \mathbb {H})$![]() the operator
the operator
1.3. $\Omega$ bounded vs $\Omega$
bounded vs $\Omega$ unbounded
unbounded
We will treat separately the cases of $\Omega$![]() bounded and of $\Omega$
bounded and of $\Omega$![]() unbounded. The unbounded case is more complicated as explained at the end of this section and needs some more constraints on the shape of $\Omega$
unbounded. The unbounded case is more complicated as explained at the end of this section and needs some more constraints on the shape of $\Omega$![]() that we now introduce. For the following definition, we shall utilize $n$
that we now introduce. For the following definition, we shall utilize $n$![]() -dimensional spherical coordinates $(r,\omega )$
-dimensional spherical coordinates $(r,\omega )$![]() where $r\geq 0$
where $r\geq 0$![]() is the distance from the origin, $\omega \in S_{n-1}$
is the distance from the origin, $\omega \in S_{n-1}$![]() , and $S_{n-1}$
, and $S_{n-1}$![]() denotes the sphere in $\mathbb {R}^{n}$
denotes the sphere in $\mathbb {R}^{n}$![]() (see [Reference Elcrat and Lean26]; in our case, however, $n=3$
(see [Reference Elcrat and Lean26]; in our case, however, $n=3$![]() ).
).
Definition 1.3 An open set $\Omega \subset \mathbb {R}^{3}$![]() is said to have the property $(R)$
is said to have the property $(R)$![]() if there exists $P\in \mathbb {R}^{3}\setminus \overline \Omega$
if there exists $P\in \mathbb {R}^{3}\setminus \overline \Omega$![]() such that every ray through $P$
such that every ray through $P$![]() has the intersection with $\Omega$
has the intersection with $\Omega$![]() which is either empty or an infinite interval. More precisely, for each $\omega \in S_2$
which is either empty or an infinite interval. More precisely, for each $\omega \in S_2$![]() set
set

We are assuming that if $f(\omega )\neq \infty$![]() , then $P+r\omega \in \Omega$
, then $P+r\omega \in \Omega$![]() for all $r\in (f(\omega ),\infty )$
for all $r\in (f(\omega ),\infty )$![]() .
.
Examples of unbounded domains, which satisfy the property $(R)$![]() are: $\Omega :=\{x\in \mathbb {R}^{3}:\, |x-P|>M\}$
are: $\Omega :=\{x\in \mathbb {R}^{3}:\, |x-P|>M\}$![]() and $\Omega :=\{x\in \mathbb {R}^{3} :\, \langle P-x,v\rangle >0\}$
and $\Omega :=\{x\in \mathbb {R}^{3} :\, \langle P-x,v\rangle >0\}$![]() where $v\in \mathbb {R}^{3}$
where $v\in \mathbb {R}^{3}$![]() is a vector, $P\in \mathbb {R}^{3}$
is a vector, $P\in \mathbb {R}^{3}$![]() is a point and $M>0$
is a point and $M>0$![]() is a positive constant (here $\langle \cdot,\cdot \rangle$
is a positive constant (here $\langle \cdot,\cdot \rangle$![]() is the standard scalar product of $\mathbb {R}^{3}$
is the standard scalar product of $\mathbb {R}^{3}$![]() ). We are ready to formulate in the precise way the problems that we have to solve.
). We are ready to formulate in the precise way the problems that we have to solve.
Problem 1.4 Let $\Omega \subset \mathbb {R}^{3}$![]() be with $C^{1}$
be with $C^{1}$![]() boundary, which is either bounded or unbounded and satisfying the property $(R)$
boundary, which is either bounded or unbounded and satisfying the property $(R)$![]() . Let $F:\Omega \to \mathbb {C}\otimes \mathbb {H}$
. Let $F:\Omega \to \mathbb {C}\otimes \mathbb {H}$![]() be a given $L^{2}$
be a given $L^{2}$![]() -function and denote by $u:\Omega \to \mathbb {C}\otimes \mathbb {H}$
-function and denote by $u:\Omega \to \mathbb {C}\otimes \mathbb {H}$![]() the unknown function satisfying the boundary value problem:
the unknown function satisfying the boundary value problem:

where ${\bf b} =(b_1,b_2,b_3)$![]() and $\partial ^{\mathbf {b}}=\partial ^{b_1}_{x_1}\partial ^{b_2}_{x_2}\partial ^{b_3}_{x_3}$
and $\partial ^{\mathbf {b}}=\partial ^{b_1}_{x_1}\partial ^{b_2}_{x_2}\partial ^{b_3}_{x_3}$![]() . Determine the conditions on the coefficients $a_1, a_2, a_3 : \Omega \to \mathbb {R}$
. Determine the conditions on the coefficients $a_1, a_2, a_3 : \Omega \to \mathbb {R}$![]() such that the boundary value problem has a unique solution in a suitable function space and, moreover, the $L^{2}$
such that the boundary value problem has a unique solution in a suitable function space and, moreover, the $L^{2}$![]() -estimates (1.6) for the $S$
-estimates (1.6) for the $S$![]() -resolvent operators hold.
-resolvent operators hold.
Remark 1.5 If $\Omega$![]() is bounded and its boundary is of class $C^{m}$
is bounded and its boundary is of class $C^{m}$![]() , the previous boundary value problem is equivalent to
, the previous boundary value problem is equivalent to

where, $\nu$![]() is the normal vector field pointing outside $\partial \Omega$
is the normal vector field pointing outside $\partial \Omega$![]() (see Theorem 7.41 in [Reference Renardy and Rogers33]).
(see Theorem 7.41 in [Reference Renardy and Rogers33]).
We are going to solve the previous problem by the use of the Lax–Milgram Lemma. In particular, to solve the boundary value problem (1.7), we want to find some conditions on the coefficients $a_j$![]() 's in a such way that the continuity and the coercivity of the quadratic form $b_s(u,v)$
's in a such way that the continuity and the coercivity of the quadratic form $b_s(u,v)$![]() associated with $\mathcal {Q}_s(T)$
associated with $\mathcal {Q}_s(T)$![]() hold (see Definition 2.3). The need of proving also the estimates (1.6) makes the assumptions on the coefficients $a_l$
hold (see Definition 2.3). The need of proving also the estimates (1.6) makes the assumptions on the coefficients $a_l$![]() 's stronger than the usual one that we have to require for the coercivity of $b_s(\cdot,\cdot )$
's stronger than the usual one that we have to require for the coercivity of $b_s(\cdot,\cdot )$![]() , since we can not rely on the term $|s|^{2}\|u\|^{2}$
, since we can not rely on the term $|s|^{2}\|u\|^{2}$![]() of $b_s(\cdot,\cdot )$
of $b_s(\cdot,\cdot )$![]() . For this reason, the other positive term in $b_s(u,u)$
. For this reason, the other positive term in $b_s(u,u)$![]() , that is $\sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|$
, that is $\sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|$![]() , has to control the $L^{2}$
, has to control the $L^{2}$![]() -norm of $u$
-norm of $u$![]() and the $L^{2}$
and the $L^{2}$![]() -norms of all the partial derivatives of $u$
-norms of all the partial derivatives of $u$![]() up to order $m-1$
up to order $m-1$![]() . In § 3, when $\Omega$
. In § 3, when $\Omega$![]() is a bounded domain of $\mathbb {R}^{3}$
is a bounded domain of $\mathbb {R}^{3}$![]() , through an iterated use of Poincaré's inequality, we will show that the conditions:
, through an iterated use of Poincaré's inequality, we will show that the conditions:
• $|a_j| \gg \max (C_\Omega ^{m}, C_\Omega )$
 ;
;• $|a_j| \gg |\partial ^{\beta } a_j|$
 for any $|\beta |< m$
for any $|\beta |< m$ ,
,
are sufficient to solve the Problem 1.4. Here and in what follows, $C_\Omega$![]() denotes the Poincaré constant of $\Omega$
denotes the Poincaré constant of $\Omega$![]() . When $\Omega$
. When $\Omega$![]() is an unbounded domain of $\mathbb {R}^{3}$
is an unbounded domain of $\mathbb {R}^{3}$![]() and $m=1$
and $m=1$![]() , the role of the Poincaré inequalities is replaced by the Gagliardo–Nirenberg estimates and a condition of integrability on the first derivatives of the coefficients is sufficient to get the coercivity of $b_s(\cdot,\cdot )$
, the role of the Poincaré inequalities is replaced by the Gagliardo–Nirenberg estimates and a condition of integrability on the first derivatives of the coefficients is sufficient to get the coercivity of $b_s(\cdot,\cdot )$![]() (see [Reference Colombo, Deniz-Gonzales and Pinton24]).
(see [Reference Colombo, Deniz-Gonzales and Pinton24]).
When $\Omega$![]() is an unbounded domain of $\mathbb {R}^{3}$
is an unbounded domain of $\mathbb {R}^{3}$![]() and the order of the operator $T$
and the order of the operator $T$![]() is greater than $1$
is greater than $1$![]() , the Gagliardo–Nirenberg estimates can not be used in an iterated way as for Poincaré's inequality. In § 2, we propose one way to overcome this problem by the use of a weighted Poincaré's inequality on some unbounded domains under an exponential decay condition at infinity of the coefficients $a_j$
, the Gagliardo–Nirenberg estimates can not be used in an iterated way as for Poincaré's inequality. In § 2, we propose one way to overcome this problem by the use of a weighted Poincaré's inequality on some unbounded domains under an exponential decay condition at infinity of the coefficients $a_j$![]() 's (see Theorem 4.3).
's (see Theorem 4.3).
In this paper, the definition of the fractional quaternionic operators is based on the $S$![]() -spectrum approach to fractional diffusion problems see [Reference Alpay, Colombo, Qian and Sabadini2, Reference Colombo and Gantner13, Reference Colombo and Gantner14]. This method is a generalization of the Balakrishnan's method to construct the fractional power of a real operator, see [Reference Balakrishnan5]. There are also several nonlinear models that involve the fractional power of scalar elliptic operators, see for example [Reference Bucur and Valdinoci11, Reference Vazquez34].
-spectrum approach to fractional diffusion problems see [Reference Alpay, Colombo, Qian and Sabadini2, Reference Colombo and Gantner13, Reference Colombo and Gantner14]. This method is a generalization of the Balakrishnan's method to construct the fractional power of a real operator, see [Reference Balakrishnan5]. There are also several nonlinear models that involve the fractional power of scalar elliptic operators, see for example [Reference Bucur and Valdinoci11, Reference Vazquez34].
2. The weak formulation of Problem 1.4
The boundary $\partial \Omega$![]() of $\Omega$
of $\Omega$![]() is assumed to be of class $C^{1}$
is assumed to be of class $C^{1}$![]() even though for some lemmas in the sequel the conditions on the open set $\Omega$
even though for some lemmas in the sequel the conditions on the open set $\Omega$![]() can be weakened. We consider the right quaternionic Hilbert space $\mathbb {C}\otimes \mathbb {H}$
can be weakened. We consider the right quaternionic Hilbert space $\mathbb {C}\otimes \mathbb {H}$![]() endowed with the scalar product
endowed with the scalar product
where $i$![]() is the imaginary unit of $\mathbb {C}$
is the imaginary unit of $\mathbb {C}$![]() , $u=q_1+i q_2$
, $u=q_1+i q_2$![]() , $v=w_1+iw_2$
, $v=w_1+iw_2$![]() and $q_1,\, q_2,\, w_1,\, w_2\in \mathbb {H}$
and $q_1,\, q_2,\, w_1,\, w_2\in \mathbb {H}$![]() . As usual, we define the modulus of $u\in \mathbb {C}\otimes \mathbb {H}$
. As usual, we define the modulus of $u\in \mathbb {C}\otimes \mathbb {H}$![]() as
as
We observe that a function $u:\Omega \to \mathbb {C}\otimes \mathbb {H}$![]() is determined by eight real functions $u_{j,l}:\Omega \to \mathbb {R}$
is determined by eight real functions $u_{j,l}:\Omega \to \mathbb {R}$![]() where $j= 0,\, 1,\, 2,\, 3$
where $j= 0,\, 1,\, 2,\, 3$![]() and $l=1,\, 2$
and $l=1,\, 2$![]() . We call these functions the components of $u$
. We call these functions the components of $u$![]() . We will use the following notation
. We will use the following notation

where $u_1(x)\,:=\,u_{0,1}(x)\,+\,u_{1,1}(x)e_1\,+\,u_{2,1}(x)e_2\,+\,u_{3,1}(x)e_3$![]() and $u_2(x):=u_{0,2}(x)+ u_{1,2}(x)e_1+u_{2,2}(x)e_2+u_{3,2}(x)e_3$
and $u_2(x):=u_{0,2}(x)+ u_{1,2}(x)e_1+u_{2,2}(x)e_2+u_{3,2}(x)e_3$![]() . We can consider the space of $L^{p}$
. We can consider the space of $L^{p}$![]() -integrable functions from a domain $\Omega \subset \mathbb {R}^{3}$
-integrable functions from a domain $\Omega \subset \mathbb {R}^{3}$![]() to $\mathbb {C}\otimes \mathbb {H}$
to $\mathbb {C}\otimes \mathbb {H}$![]()
The space $L^{2}$![]() with the scalar product:
with the scalar product:
is a right linear quaternionic Hilbert space. We furthermore introduce the quaternionic Sobolev space of order $m$![]()

where the space $H^{m}(\Omega,\mathbb {R})$![]() is the Sobolev space of order $m$
is the Sobolev space of order $m$![]() defined as in [Reference Evans25] Chapter $5$
defined as in [Reference Evans25] Chapter $5$![]() . We have that $H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$
. We have that $H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() endowed with the quaternionic scalar product
endowed with the quaternionic scalar product

where $\mathbf {b}\in \mathbb {N}^{3}$![]() , becomes a right linear quaternionic Hilbert space. As usual the space $H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$
, becomes a right linear quaternionic Hilbert space. As usual the space $H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() is the closure of the space $C^{\infty }_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
is the closure of the space $C^{\infty }_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() in $H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$
in $H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() with respect to the norm $\|\cdot \|_{H^{m}}$
with respect to the norm $\|\cdot \|_{H^{m}}$![]() . This space can be characterized as the set of all functions $u\in H^{m}$
. This space can be characterized as the set of all functions $u\in H^{m}$![]() such that $\operatorname {Tr}(\partial ^{\mathbf{b}} u)= 0$
such that $\operatorname {Tr}(\partial ^{\mathbf{b}} u)= 0$![]() for any multiindex $\mathbf {b}\in \mathbb {N}^{3}$
for any multiindex $\mathbf {b}\in \mathbb {N}^{3}$![]() with $|\mathbf {b}|\leq m-1$
with $|\mathbf {b}|\leq m-1$![]() (here the trace operator $\operatorname {Tr}(\cdot )$
(here the trace operator $\operatorname {Tr}(\cdot )$![]() is defined as in [Reference Evans25] Chapter $5$
is defined as in [Reference Evans25] Chapter $5$![]() ). Now we give to the problem (1.4) the weak formulation in order to apply the Lax–Milgram lemma in the space $H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$
). Now we give to the problem (1.4) the weak formulation in order to apply the Lax–Milgram lemma in the space $H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() .
.
Remark 2.1 When $\Omega$![]() is bounded, we can endow $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
is bounded, we can endow $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() with the scalar product
with the scalar product

The $H^{m}$![]() -norm is equivalent to the norm
-norm is equivalent to the norm

This is a consequence of the following estimates
where the second inequality is obtained by Poincaré's inequality applied repeatedly to the term $\|\partial ^{\mathbf {b}} u\|_{L^{2}}$![]() for $|\mathbf {b}|< m$
for $|\mathbf {b}|< m$![]() and
and
The constant $K(m)$![]() represents the maximum number of times that $\|\partial ^{\mathbf {b}} u\|$
represents the maximum number of times that $\|\partial ^{\mathbf {b}} u\|$![]() for some $|\mathbf {b}|=m$
for some $|\mathbf {b}|=m$![]() appear on the left-hand side of the second inequality after the use of the Poincaré's inequality. The last estimate follows using the Fourier transform on the terms $\partial ^{\mathbf {b}} u$
appear on the left-hand side of the second inequality after the use of the Poincaré's inequality. The last estimate follows using the Fourier transform on the terms $\partial ^{\mathbf {b}} u$![]() when $|\mathbf {b}|=m$
when $|\mathbf {b}|=m$![]() and since there exists a positive constant $K>0$
and since there exists a positive constant $K>0$![]() such that
such that

(we can use the Fourier transform since any $u\in H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() can be extended by $0$
can be extended by $0$![]() outside $\Omega$
outside $\Omega$![]() preserving the $H^{m}$
preserving the $H^{m}$![]() -regularity in $\mathbb {R}^{3}$
-regularity in $\mathbb {R}^{3}$![]() ). We define the constant $K(m,\Omega ):=KK(m)K_\Omega$
). We define the constant $K(m,\Omega ):=KK(m)K_\Omega$![]() (we will use several times this constant in the sequel and according to our necessity it could be rescaled by other constants which depends on $m$
(we will use several times this constant in the sequel and according to our necessity it could be rescaled by other constants which depends on $m$![]() ). When $\Omega$
). When $\Omega$![]() is unbounded $\|\cdot \|_{D^{m}}$
is unbounded $\|\cdot \|_{D^{m}}$![]() is not a norm, still we will use several times the estimate
is not a norm, still we will use several times the estimate
Remark 2.2 We will use several times a classical argument of integration by parts that we describe now. Let $f_1,\, f_2\in H^{k}_0(\Omega,\mathbb {R})$![]() and $\partial ^{\mathbf{b}} f_3,\, \partial ^{\mathbf{b}} f_4\in L^{2}(\Omega )\cap L^{\infty }(\Omega )$
and $\partial ^{\mathbf{b}} f_3,\, \partial ^{\mathbf{b}} f_4\in L^{2}(\Omega )\cap L^{\infty }(\Omega )$![]() for any $\mathbf {b}\in \mathbb {N}^{3}$
for any $\mathbf {b}\in \mathbb {N}^{3}$![]() with $|\mathbf {b}|\leq k$
with $|\mathbf {b}|\leq k$![]() then, integrating by parts $k$
then, integrating by parts $k$![]() -times and recalling that the traces at the boundary of $\partial ^{\mathbf{b}} f_2$
-times and recalling that the traces at the boundary of $\partial ^{\mathbf{b}} f_2$![]() for all $|\mathbf {b}|< k$
for all $|\mathbf {b}|< k$![]() are zero, we have that for any $i=1,\, 2,\, 3$
are zero, we have that for any $i=1,\, 2,\, 3$![]()

where $\mathbf {t}=(t_1,t_2,t_3)\in \mathbb {N}^{3}$![]() and $\begin {pmatrix} k\\ \mathbf {t}\end {pmatrix}=\frac {k!}{t_1!t_2!t_3!}$
and $\begin {pmatrix} k\\ \mathbf {t}\end {pmatrix}=\frac {k!}{t_1!t_2!t_3!}$![]() .
.
From Definition 1.2, we have

where $\begin {pmatrix}m\\k\end {pmatrix}=\frac {m!}{k!(m-k)!}$![]() , and the scalar part of $\mathcal {Q}_s(T)$
, and the scalar part of $\mathcal {Q}_s(T)$![]() is
is

while the vectorial part is

We consider the bilinear form
for functions $u,\, v\in C^{2m}_0(\overline {\Omega },\mathbb {C}\otimes \mathbb {H})$![]() . Note that
. Note that
Using Remark 2.2, we have that

where $\mathbf {t}'=(t_1',t_2')\in \mathbb {N}^{2}$![]() and also
and also

Relying on the above considerations we can give the following two definitions.
Definition 2.3 Let $\Omega$![]() be a bounded domain (or an unbounded domain) in $\mathbb {R}^{3}$
be a bounded domain (or an unbounded domain) in $\mathbb {R}^{3}$![]() with the boundary $\partial \Omega$
with the boundary $\partial \Omega$![]() of class $C^{1}$
of class $C^{1}$![]() , let $a_1$
, let $a_1$![]() , $a_2$
, $a_2$![]() , $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})$
, $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})$![]() (or in the case of the unbounded domains $a_1$
(or in the case of the unbounded domains $a_1$![]() , $a_2$
, $a_2$![]() , $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})\cap L^{\infty }(\Omega )$
, $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})\cap L^{\infty }(\Omega )$![]() such that $\partial ^{\mathbf{b}} a_j\in L^{\infty }(\Omega )$
such that $\partial ^{\mathbf{b}} a_j\in L^{\infty }(\Omega )$![]() for any $j=1,\, 2,\, 3$
for any $j=1,\, 2,\, 3$![]() and for any $\mathbf {b}\in \mathbb {N}^{3}$
and for any $\mathbf {b}\in \mathbb {N}^{3}$![]() such that $|\mathbf {b}|\leq m$
such that $|\mathbf {b}|\leq m$![]() ). We define the bilinear form:
). We define the bilinear form:

for all functions $u,v \in H_0^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() .
.
Definition 2.4 Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{3}$
be a bounded domain in $\mathbb {R}^{3}$![]() with $C^{1}$
with $C^{1}$![]() boundary (or an unbounded domain which satisfy property $(R)$
boundary (or an unbounded domain which satisfy property $(R)$![]() ). We say that $u\in H^{m}_0$
). We say that $u\in H^{m}_0$![]() is the weak solution of the existence problem in 1.4 for some $s\in \mathbb {H}$
is the weak solution of the existence problem in 1.4 for some $s\in \mathbb {H}$![]() and a given $F\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$
and a given $F\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() , if we have
, if we have
where $b_s$![]() is the bilinear form defined in Definition 2.3.
is the bilinear form defined in Definition 2.3.
3. Weak solution of Problem 1.4 when $\Omega$ is bounded
is bounded
To prove the existence and uniqueness of the weak solutions of the Problem 1.4 in the case $\Omega$![]() is bounded, it will be sufficient to show that the bilinear forms $b_s(\cdot,\cdot )$
is bounded, it will be sufficient to show that the bilinear forms $b_s(\cdot,\cdot )$![]() , in Definition 2.3, are continuous and coercive in $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
, in Definition 2.3, are continuous and coercive in $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() .
.
First, we prove the continuity in § 3.1. The coercivity will be proved in § 3.2 when $s=js_1$![]() for $j\in \mathbb {S}$
for $j\in \mathbb {S}$![]() and $s_1\in \mathbb {R}$
and $s_1\in \mathbb {R}$![]() with $s_1\neq 0$
with $s_1\neq 0$![]() . As a direct consequence of the coercivity, we will prove an $L^{2}$
. As a direct consequence of the coercivity, we will prove an $L^{2}$![]() estimate for the weak solution $u$
estimate for the weak solution $u$![]() that belongs to $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
that belongs to $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() and also we will prove an $L^{2}$
and also we will prove an $L^{2}$![]() estimate for the term $T(u)$
estimate for the term $T(u)$![]() .
.
3.1. The continuity of the bilinear form $b_s(\cdot,\cdot )$
The bilinear form
for some $s\in \mathbb {H}$![]() , is continuous if there exists a positive constant $C(s)$
, is continuous if there exists a positive constant $C(s)$![]() such that
such that
We note that the constant $C(s)$![]() depends on $s\in \mathbb {H}$
depends on $s\in \mathbb {H}$![]() but does not depend on $u$
but does not depend on $u$![]() and $v\in H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$
and $v\in H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() .
.
Proposition 3.1 Continuity of $b_s$![]()
Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{3}$
be a bounded domain in $\mathbb {R}^{3}$![]() with boundary $\partial \Omega$
with boundary $\partial \Omega$![]() of class $C^{1}$
of class $C^{1}$![]() . Assume that $a_1,$
. Assume that $a_1,$![]() $a_2,$
$a_2,$![]() $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})$
$a_3\in C^{m}(\overline {\Omega }, \mathbb {R})$![]() then we have
then we have




The previous constants can be estimated as follows

where the constant $C$![]() is the sum of the maximum of the integrals in the inequalities (3.2), (3.3) and (3.4).
is the sum of the maximum of the integrals in the inequalities (3.2), (3.3) and (3.4).
Moreover, for any $s\in \mathbb {H}$![]() there exists a positive constant $C(s)$
there exists a positive constant $C(s)$![]() such that for any $(u,v)\in H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})\times H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$
such that for any $(u,v)\in H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})\times H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() , the bilinear form $b_s(\cdot,\cdot )$
, the bilinear form $b_s(\cdot,\cdot )$![]() satisfies the estimate
satisfies the estimate
that is, $b_s(\cdot,\cdot )$![]() is a continuous bilinear form.
is a continuous bilinear form.
Proof. The inequality (3.1) is a direct consequence of the boundedness of the coefficients $a_l$![]() 's and the Hölder inequality. The estimates (3.2), (3.3) and (3.4) can be proved in a similar way and so we briefly explain how to prove the inequality (3.2). First, to each integral that is on the left-hand side of the equation, we repeatedly apply Hölder's and Poincaré's inequalities. In this way, each integral can be estimated by a constant depending on the sup norm of $\partial _{x_l}^{s} a_t$
's and the Hölder inequality. The estimates (3.2), (3.3) and (3.4) can be proved in a similar way and so we briefly explain how to prove the inequality (3.2). First, to each integral that is on the left-hand side of the equation, we repeatedly apply Hölder's and Poincaré's inequalities. In this way, each integral can be estimated by a constant depending on the sup norm of $\partial _{x_l}^{s} a_t$![]() 's times $\|u\|_{D^{m}}\|v\|_{D^{m}}$
's times $\|u\|_{D^{m}}\|v\|_{D^{m}}$![]() . Second, we sum up term by term. Finally, the continuity of $b_s(\cdot,\cdot )$
. Second, we sum up term by term. Finally, the continuity of $b_s(\cdot,\cdot )$![]() is a direct consequence of the previous estimates.
is a direct consequence of the previous estimates.
3.2. Weak solution of the Problem 1.4
Theorem 3.2 Let $\Omega$![]() be a bounded domain in $\mathbb {R}^{3}$
be a bounded domain in $\mathbb {R}^{3}$![]() with boundary $\partial \Omega$
with boundary $\partial \Omega$![]() of class $C^{1}$
of class $C^{1}$![]() . Let $T$
. Let $T$![]() be the operator defined in (1.2) with coefficients $a_1,$
be the operator defined in (1.2) with coefficients $a_1,$![]() $a_2,$
$a_2,$![]() $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})$
$a_3\in C^{m}(\overline {\Omega }, \mathbb {R})$![]() and set
and set

Suppose
then:
(I) The boundary value Problem (1.4) has a unique weak solution $u\in H^{m}_0(\Omega,\mathbb {H}),$
 for $s\in \mathbb {H}\setminus \{0\}$
for $s\in \mathbb {H}\setminus \{0\}$ with $\mathrm {Re}(s)=0,$
with $\mathrm {Re}(s)=0,$ and
(3.7)\begin{equation} \|u\|^{2}_{L^{2}}\leq \displaystyle\frac 1{|s|^{2}} \mathrm{Re}(b_s(u,u)). \end{equation}
and
(3.7)\begin{equation} \|u\|^{2}_{L^{2}}\leq \displaystyle\frac 1{|s|^{2}} \mathrm{Re}(b_s(u,u)). \end{equation}
(II) The following estimate holds
for every $u\in H^{1}_0(\Omega,\mathbb {H}),$![]() and $s\in \mathbb {H}\setminus \{0\}$
and $s\in \mathbb {H}\setminus \{0\}$![]() with $\mathrm {Re}(s)=0,$
with $\mathrm {Re}(s)=0,$![]() where
where
Observe that we assume that the minimum of each $a_l^{2}(x)$![]() for $x\in \overline {\Omega }$
for $x\in \overline {\Omega }$![]() is strictly positive and in fact greater than $2M$
is strictly positive and in fact greater than $2M$![]() . This fact can always be achieved by modifying $T$
. This fact can always be achieved by modifying $T$![]() by adding a suitable constant to each coefficients $a_l$
by adding a suitable constant to each coefficients $a_l$![]() of $T$
of $T$![]() , $l=1,2,3$
, $l=1,2,3$![]() .
.
Proof. In order to use the Lax–Milgram Lemma to prove the existence and the uniqueness of the solution for the weak formulation of the problem, it is sufficient to prove the coercivity of the bilinear form $b_s(\cdot,\cdot )$![]() in Definition 2.1 since the continuity is proved in Proposition 3.1. First, we write explicitly ${\rm Re}\, b_{js_1}(u,u)$
in Definition 2.1 since the continuity is proved in Proposition 3.1. First, we write explicitly ${\rm Re}\, b_{js_1}(u,u)$![]() , where we have set $s=js_1$
, where we have set $s=js_1$![]() , for $s_1\in \mathbb {R}$
, for $s_1\in \mathbb {R}$![]() and $j\in \mathbb {S}$
and $j\in \mathbb {S}$![]() :
:

We see that the first two terms are positive. What remain to estimate are the three summations of the integrals in (3.9). Since they can be treated in the same way, we explain in detail the estimate for the second. By Hölder's inequality and the repeatedly use of Poincaré's inequality, we have for $t_1=0$![]()

In the case $t_1\neq 0$![]() , since $k>0$
, since $k>0$![]() , we have
, we have

Summing up all the previous estimates of the terms in the second summation and rescaling the constants $K(m,\Omega )$![]() multiplying it by a constant which depends only on $m$
multiplying it by a constant which depends only on $m$![]() , we obtain
, we obtain

Analogous estimates also hold for the other summation of integrals. Eventually, summing up all the estimates, choosing $\epsilon$![]() in such a way that $\sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|^{2}-C\epsilon \sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|^{2}\geq \frac 12 \sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|^{2}$
in such a way that $\sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|^{2}-C\epsilon \sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|^{2}\geq \frac 12 \sum _{l=1}^{3}\|a_l\partial _{x_l}^{m} u\|^{2}$![]() (where $C$
(where $C$![]() depends only on $m$
depends only on $m$![]() ) and uniformazing the constants $K(m,\Omega )$
) and uniformazing the constants $K(m,\Omega )$![]() , we obtain
, we obtain

and, moreover,
Thus, the quadratic form $b_{js_1}(\cdot,\cdot )$![]() is coercive for every $s_1\in \mathbb {R}$
is coercive for every $s_1\in \mathbb {R}$![]() . In particular, we have
. In particular, we have
By the Lax–Milgram Lemma, we have that for any $w\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() there exists $u_w\in H^{m}_0(\Omega,\mathbb {H})$
there exists $u_w\in H^{m}_0(\Omega,\mathbb {H})$![]() , for $s_1\in \mathbb {R}\setminus \{0\}$
, for $s_1\in \mathbb {R}\setminus \{0\}$![]() and $j\in \mathbb {S}$
and $j\in \mathbb {S}$![]() , such that
, such that
What remains to prove is the inequality (3.8). Applying the first of the inequalities in (3.10) and observing that

we have:

where the second inequality is due to the fact that $C_T^{-1}a^{2}_\ell (x)\geq 1$![]() for any $x\in \Omega$
for any $x\in \Omega$![]() , the fourth inequality is due to the fact that $\|Tu\|_{L^{2}}^{2}\leq 3 \sum _{\ell =1}^{3}\| a_\ell \partial _{x_\ell }^{m} u\|^{2}_{L^{2}}$
, the fourth inequality is due to the fact that $\|Tu\|_{L^{2}}^{2}\leq 3 \sum _{\ell =1}^{3}\| a_\ell \partial _{x_\ell }^{m} u\|^{2}_{L^{2}}$![]() and we have set
and we have set
This concludes the proof.
4. Weak solution of the Problem 1.4 for unbounded $\Omega$
To prove the existence and uniqueness of the weak solutions of the Problem 1.4 in the case of $\Omega$![]() unbounded, we proceed as in the previous section.
unbounded, we proceed as in the previous section.
First, we prove the continuity in § 4.1. The coercivity will be proved in § 4.2 when $s=js_1$![]() for $j\in \mathbb {S}$
for $j\in \mathbb {S}$![]() and $s_1\in \mathbb {R}$
and $s_1\in \mathbb {R}$![]() with $s_1\neq 0$
with $s_1\neq 0$![]() . As a direct consequence of the coercivity, we will prove an $L^{2}$
. As a direct consequence of the coercivity, we will prove an $L^{2}$![]() estimate for the weak solution $u$
estimate for the weak solution $u$![]() that belongs to $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
that belongs to $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() and also we will prove an $L^{2}$
and also we will prove an $L^{2}$![]() estimate for the term $T(u)$
estimate for the term $T(u)$![]() .
.
4.1. The continuity of the bilinear form $b_s(\cdot,\cdot )$
The bilinear form
for some $s\in \mathbb {H}$![]() , is continuous if there exists a positive constant $C(s)$
, is continuous if there exists a positive constant $C(s)$![]() such that
such that
We note that the constant $C(s)$![]() depends on $s\in \mathbb {H}$
depends on $s\in \mathbb {H}$![]() but does not depend on $u$
but does not depend on $u$![]() and $v\in H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$
and $v\in H^{m}(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() .
.
Proposition 4.1 Continuity of $b_s$![]()
Let $\Omega$![]() be an unbounded domain in $\mathbb {R}^{3}$
be an unbounded domain in $\mathbb {R}^{3}$![]() with boundary $\partial \Omega$
with boundary $\partial \Omega$![]() of class $C^{1}$
of class $C^{1}$![]() . Assume that $a_1,$
. Assume that $a_1,$![]() $a_2,$
$a_2,$![]() $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})\cap L^{\infty }(\Omega )$
$a_3\in C^{m}(\overline {\Omega }, \mathbb {R})\cap L^{\infty }(\Omega )$![]() and that $\partial ^{\beta } a_j\in L^{\infty }(\Omega )$
and that $\partial ^{\beta } a_j\in L^{\infty }(\Omega )$![]() for any $j=1,\, 2,\, 3$
for any $j=1,\, 2,\, 3$![]() and for any $\beta \in \mathbb {N}^{3},$
and for any $\beta \in \mathbb {N}^{3},$![]() $|\beta |\leq m$
$|\beta |\leq m$![]() . Then we have
. Then we have




where the previous constants can be estimated as follows

where the constant $C$![]() is the sum of the maximum of the integrals in the inequalities (3.2), (3.3) and (3.4).
is the sum of the maximum of the integrals in the inequalities (3.2), (3.3) and (3.4).
Moreover, for any $s\in \mathbb {H}$![]() there exists a positive constant $C(s)$
there exists a positive constant $C(s)$![]() such that for any $(u,v)\in H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})\times H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$
such that for any $(u,v)\in H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})\times H^{m}_0(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() , the bilinear form $b_s(\cdot,\cdot )$
, the bilinear form $b_s(\cdot,\cdot )$![]() satisfies the estimate
satisfies the estimate
i.e., $b_s(\cdot,\cdot )$![]() is a continuous bilinear form.
is a continuous bilinear form.
Proof. The inequality (4.1) is a direct consequence of the boundedness of the coefficients $a_l$![]() 's and the Hölder inequality. The estimates (4.2), (4.3) and (4.4) can be proved in a similar way and so we briefly explain how to prove the inequality (4.2). First we apply the Hölder inequality to each integral that belongs to the left-hand side. Thus, each integral can be estimated by a constant (that depends on the sup norm of $\partial _{x_l}^{s} a_t$
's and the Hölder inequality. The estimates (4.2), (4.3) and (4.4) can be proved in a similar way and so we briefly explain how to prove the inequality (4.2). First we apply the Hölder inequality to each integral that belongs to the left-hand side. Thus, each integral can be estimated by a constant (that depends on the sup norm of $\partial _{x_l}^{s} a_t$![]() 's) times $\|\partial ^{m}_{x_l} u\|\|\partial ^{\beta } v\|$
's) times $\|\partial ^{m}_{x_l} u\|\|\partial ^{\beta } v\|$![]() for $|\beta |\leq m$
for $|\beta |\leq m$![]() and $l=1,\, 2,\, 3$
and $l=1,\, 2,\, 3$![]() . Since $\|\partial ^{m}_{x_l} u\|\|\partial ^{\beta } v\|\leq \|u\|_{H^{m}}\|v\|_{H^{m}}$
. Since $\|\partial ^{m}_{x_l} u\|\|\partial ^{\beta } v\|\leq \|u\|_{H^{m}}\|v\|_{H^{m}}$![]() for any $|\beta |\leq m$
for any $|\beta |\leq m$![]() and $j=1,\,2,\, 3$
and $j=1,\,2,\, 3$![]() , we sum up term by term to get the desired estimate. Eventually, the continuity of $b_s(\cdot,\cdot )$
, we sum up term by term to get the desired estimate. Eventually, the continuity of $b_s(\cdot,\cdot )$![]() is a direct consequence of the previous estimates.
is a direct consequence of the previous estimates.
4.2. Weak solution of the Problem 1.4
For the coercivity, we need the following results (see [Reference Elcrat and Lean26]), which are the corresponding of Poincaré's inequality in the case of the unbounded domains.
Theorem 4.2 Let $\Omega$![]() be a domain in $\mathbb {R}^{3}$
be a domain in $\mathbb {R}^{3}$![]() which satisfies the property $(R)$
which satisfies the property $(R)$![]() . Let $\phi \in C^{1}(\overline \Omega )$
. Let $\phi \in C^{1}(\overline \Omega )$![]() be a bounded positive function for which there exists a positive constant $\lambda$
be a bounded positive function for which there exists a positive constant $\lambda$![]() such that
such that
for all $\omega \in \mathbb {S}^{2}$![]() . Then for each $u\in C^{\infty }_0(\Omega,\mathbb {R})$
. Then for each $u\in C^{\infty }_0(\Omega,\mathbb {R})$![]() and any $(1\leq p<\infty )$
and any $(1\leq p<\infty )$![]() , we have
, we have
We call $\phi$![]() a weight function for $\Omega$
a weight function for $\Omega$![]() with a rate of exponentially decaying $\lambda$
with a rate of exponentially decaying $\lambda$![]() . As explained in [Reference Elcrat and Lean26], we can observe that the graph of $\phi$
. As explained in [Reference Elcrat and Lean26], we can observe that the graph of $\phi$![]() has the shape of an exponentially decaying hill. An example of a weight function for all the domains which satisfy the property $(R)$
has the shape of an exponentially decaying hill. An example of a weight function for all the domains which satisfy the property $(R)$![]() is
is
If the domain is contained in a half-space, after an affine changing of variables, we can suppose that it is contained in $\{x\in \mathbb {R}^{3}:\, x_1>0\}$![]() . The previous theorem holds also requiring the weight function $\phi$
. The previous theorem holds also requiring the weight function $\phi$![]() satisfies the assumption
satisfies the assumption
instead of the assumption (4.6). In this case, the graph of $\phi$![]() has the shape of an exponentially decaying ridge and an example of this kind of function is
has the shape of an exponentially decaying ridge and an example of this kind of function is
Theorem 4.3 Let $\Omega$![]() be an unbounded domain in $\mathbb {R}^{3}$
be an unbounded domain in $\mathbb {R}^{3}$![]() such that it satisfies the property $(R)$
such that it satisfies the property $(R)$![]() and with its boundary $\partial \Omega$
and with its boundary $\partial \Omega$![]() of class $C^{1}$
of class $C^{1}$![]() . Let $\phi$
. Let $\phi$![]() be a bounded weight function for $\Omega$
be a bounded weight function for $\Omega$![]() with the rate of exponential decay $\lambda$
with the rate of exponential decay $\lambda$![]() . Let $T$
. Let $T$![]() be the operator defined in (1.2) with coefficients $a_1,$
be the operator defined in (1.2) with coefficients $a_1,$![]() $a_2,$
$a_2,$![]() $a_3\in C^{m}(\overline {\Omega }, \mathbb {R})\cap L^{\infty }(\Omega )$
$a_3\in C^{m}(\overline {\Omega }, \mathbb {R})\cap L^{\infty }(\Omega )$![]() such that $|\partial _{x_l}^{t} a_j(x)|^{2}\leq C \phi$
such that $|\partial _{x_l}^{t} a_j(x)|^{2}\leq C \phi$![]() for some positive constant $C$
for some positive constant $C$![]() and for all $t=1,\, \ldots, \, m$
and for all $t=1,\, \ldots, \, m$![]() and $j,\,l=1,\, 2,\, 3$
and $j,\,l=1,\, 2,\, 3$![]() . We set
. We set
where $K(m)$![]() and $K(m,\phi,\lambda )$
and $K(m,\phi,\lambda )$![]() are positive constants that depend on the order $m$
are positive constants that depend on the order $m$![]() of the operator, on $\phi$
of the operator, on $\phi$![]() and on $\lambda$
and on $\lambda$![]() . We suppose that
. We suppose that
Then:
(I) The boundary value Problem (1.4) has a unique weak solution $u\in H^{m}_0(\Omega,\mathbb {H}\otimes \mathbb {C})$
 , for $s\in \mathbb {H}\setminus \{0\}$
, for $s\in \mathbb {H}\setminus \{0\}$ with $\mathrm {Re}(s)=0$
with $\mathrm {Re}(s)=0$ , and
(4.8)\begin{equation} \|u\|^{2}_{L^{2}}\leq \displaystyle\frac 1{|s|^{2}} \mathrm{Re}(b_s(u,u)). \end{equation}
, and
(4.8)\begin{equation} \|u\|^{2}_{L^{2}}\leq \displaystyle\frac 1{|s|^{2}} \mathrm{Re}(b_s(u,u)). \end{equation}
(II) Moreover, we have the following estimate
for every $u\in H^{m}_0(\Omega,\mathbb {H}),$![]() and $s\in \mathbb {H}\setminus \{0\}$
and $s\in \mathbb {H}\setminus \{0\}$![]() with $\mathrm {Re}(s)=0,$
with $\mathrm {Re}(s)=0,$![]() where
where
Proof. In order to use the Lax–Milgram Lemma to prove the existence and the uniqueness of the solution for the weak formulation of the problem, it is sufficient to prove the coercivity of the bilinear form $b_s(\cdot,\cdot )$![]() in Definition 2.1 since the continuity is proved in Proposition 4.1. First, we write explicitly ${\rm Re}\, b_{{\bf j}s_1}(u,u)$
in Definition 2.1 since the continuity is proved in Proposition 4.1. First, we write explicitly ${\rm Re}\, b_{{\bf j}s_1}(u,u)$![]() , where we have set $s={\bf j}s_1$
, where we have set $s={\bf j}s_1$![]() , for $s_1\in \mathbb {R}$
, for $s_1\in \mathbb {R}$![]() and ${\bf j}\in \mathbb {S}$
and ${\bf j}\in \mathbb {S}$![]() :
:

We see that the first two terms in (4.10) are positive. The other terms, that we have collected in four summations, can be estimated all in the same way and for this reason we explain how to estimate only the integrals in the first summation. By Hölder's inequality and the repeated application of Theorem 4.2, we have for $k=0$![]() or $k=t_1$
or $k=t_1$![]()

where the constants $C$![]() , $C'$
, $C'$![]() and $C''$
and $C''$![]() depend on $\phi$
depend on $\phi$![]() , the derivatives of $a_j$
, the derivatives of $a_j$![]() 's and $m$
's and $m$![]() . In the case $0< k< t_1$
. In the case $0< k< t_1$![]() , we have
, we have

Summing up all the previous inequalities and choosing the constants $k(m)$![]() and $k(m,\phi,\lambda )$
and $k(m,\phi,\lambda )$![]() in a suitable way, we obtain
in a suitable way, we obtain

We note that $K(m,\phi,\lambda )$![]() depends on $\lambda$
depends on $\lambda$![]() through the multiplicative constant $\max ((\frac 2\lambda )^{2m},\,(\frac 2\lambda )^{2})$
through the multiplicative constant $\max ((\frac 2\lambda )^{2m},\,(\frac 2\lambda )^{2})$![]() . Analogous estimates also holds for the other summation of integrals (here the role of $k$
. Analogous estimates also holds for the other summation of integrals (here the role of $k$![]() is played by $t_1$
is played by $t_1$![]() and thus, we have to distinguish the cases of $t_1=0$
and thus, we have to distinguish the cases of $t_1=0$![]() and $t_1\neq 0$
and $t_1\neq 0$![]() ) with possibly different constants $K(m)$
) with possibly different constants $K(m)$![]() and $K(m,\phi )$
and $K(m,\phi )$![]() . Summing up all the estimates and choosing in the right way $\epsilon$
. Summing up all the estimates and choosing in the right way $\epsilon$![]() , we obtain
, we obtain

By hypothesis (4.7), we know that
thus, the quadratic form $b_{{\bf j}s_1}(\cdot,\cdot )$![]() is coercive for every $s_1\in \mathbb {R}$
is coercive for every $s_1\in \mathbb {R}$![]() . In particular, we have
. In particular, we have
By the Lax–Milgram Lemma, we have that for any $w\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() , there exists $u_w\in H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
, there exists $u_w\in H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() , for $s_1\in \mathbb {R}\setminus \{0\}$
, for $s_1\in \mathbb {R}\setminus \{0\}$![]() and ${\bf j}\in \mathbb {S}$
and ${\bf j}\in \mathbb {S}$![]() , such that
, such that
What remains to prove is the inequality (4.9). Applying the first of the inequalities in (4.11) and observing that

we have:

where the second inequality is due to the fact that $C_T^{-1}a^{2}_\ell (x)\geq 1$![]() for any $x\in \Omega$
for any $x\in \Omega$![]() , the fourth inequality is due to the fact that $\|Tu\|_{L^{2}}^{2}\leq 3 \sum _{\ell =1}^{3}\| a_\ell \partial _{x_\ell }^{m} u\|^{2}_{L^{2}}$
, the fourth inequality is due to the fact that $\|Tu\|_{L^{2}}^{2}\leq 3 \sum _{\ell =1}^{3}\| a_\ell \partial _{x_\ell }^{m} u\|^{2}_{L^{2}}$![]() and we have set
and we have set
This concludes the proof.
Remark 4.4 We provide here two examples of domains and coefficients $a_l$![]() 's that satisfy the hypothesis of Theorem 4.3.
's that satisfy the hypothesis of Theorem 4.3.
• Let $\Omega :=\{x\in \mathbb {R}^{3}:\, |x-P|>M \}$
 and $\phi (x):=\frac {e^{-\lambda |x-P|}}{|x-P|^{2}}$
and $\phi (x):=\frac {e^{-\lambda |x-P|}}{|x-P|^{2}}$ , we define $a_l(x):= K_l+e^{-\lambda |x-P|}s_l(x)$
, we define $a_l(x):= K_l+e^{-\lambda |x-P|}s_l(x)$ where $s_l\in \mathcal {S}(\mathbb {R}^{3})$
where $s_l\in \mathcal {S}(\mathbb {R}^{3})$ and $K_l$
and $K_l$ is a positive constant large enough for $l=1,\, 2,\,3$
is a positive constant large enough for $l=1,\, 2,\,3$ ($\mathcal {S}(\mathbb {R}^{3}$
($\mathcal {S}(\mathbb {R}^{3}$ ) is the space of the Schwartz functions). By the properties of the Schwartz functions we have that
\begin{align*} \sup_{x\in\Omega}\left(\left|\frac{\partial^{\mathbf{b}} (a_l(x))}{\phi(x)}\right|\right)\leq C_{\mathbf{b},s_l},\quad\forall \, \mathbf{b}\in\mathbb{N}^{3}\quad\textrm{and}\quad |\mathbf{b}|>0. \end{align*}
) is the space of the Schwartz functions). By the properties of the Schwartz functions we have that
\begin{align*} \sup_{x\in\Omega}\left(\left|\frac{\partial^{\mathbf{b}} (a_l(x))}{\phi(x)}\right|\right)\leq C_{\mathbf{b},s_l},\quad\forall \, \mathbf{b}\in\mathbb{N}^{3}\quad\textrm{and}\quad |\mathbf{b}|>0. \end{align*}
• Let $\Omega :=\{x\in \mathbb {R}^{3}:\, \langle x-P, v\rangle >0 \}$
 and $\phi (x):=e^{-\lambda \langle x-P, v\rangle }$
and $\phi (x):=e^{-\lambda \langle x-P, v\rangle }$ , we define $a_l(x):= K+e^{-\lambda \langle x-P, v\rangle }$
, we define $a_l(x):= K+e^{-\lambda \langle x-P, v\rangle }$ where $K$
where $K$ is a positive constant large enough.
is a positive constant large enough.
5. The estimates for the $S$ -resolvent operators and the fractional powers of $T$
-resolvent operators and the fractional powers of $T$
Using the estimates in Theorem 4.3, we can now show that the $S$![]() -resolvent operator of $T$
-resolvent operator of $T$![]() decays fast enough along the set of purely imaginary quaternions.
decays fast enough along the set of purely imaginary quaternions.
Theorem 5.1 Under the hypotheses of Theorem 3.2 or of Theorem 4.3, the operator $\mathcal {Q}_s(T)$![]() is invertible for any $s={\bf j}s_1,$
is invertible for any $s={\bf j}s_1,$![]() for $s_1\in \mathbb {R}\setminus \{0\}$
for $s_1\in \mathbb {R}\setminus \{0\}$![]() and ${\bf j}\in \mathbb {S}$
and ${\bf j}\in \mathbb {S}$![]() and the following estimate
and the following estimate
holds. Moreover, the $\mathcal {S}$![]() -resolvent operators satisfy the estimates
-resolvent operators satisfy the estimates
for any $s={\bf j}s_1,$![]() for $s_1\in \mathbb {R}\setminus \{0\}$
for $s_1\in \mathbb {R}\setminus \{0\}$![]() and ${\bf j}\in \mathbb {S},$
and ${\bf j}\in \mathbb {S},$![]() with a constant $\Theta$
with a constant $\Theta$![]() that does not depend on $s$
that does not depend on $s$![]() .
.
Proof. We saw in Theorem 3.2 or in Theorem 4.3 that for all $w\in L^{2}(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() there exists $u_w\in H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
there exists $u_w\in H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() ), for $s_1\in \mathbb {R}\setminus \{0\}$
), for $s_1\in \mathbb {R}\setminus \{0\}$![]() and ${\bf j}\in \mathbb {S}$
and ${\bf j}\in \mathbb {S}$![]() , such that
, such that
Thus, we can define the inverse operator $\mathcal {Q}_{{\bf j}s_1}(T)^{-1}(w):=u_w$![]() for any $w\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$
for any $w\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() (we note that the range of $\mathcal {Q}_{{\bf j}s_1}(T)^{-1}$
(we note that the range of $\mathcal {Q}_{{\bf j}s_1}(T)^{-1}$![]() is in $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$
is in $H^{m}_0(\Omega,\mathbb {C}\otimes \mathbb {H})$![]() ). The first inequality (3.11) (or the first inequality in (4.12) in the case $\Omega$
). The first inequality (3.11) (or the first inequality in (4.12) in the case $\Omega$![]() unbounded), applied to $u:=\mathcal {Q}_{{\bf j}s_1}(T)^{-1}(w)$
unbounded), applied to $u:=\mathcal {Q}_{{\bf j}s_1}(T)^{-1}(w)$![]() , implies:
, implies:

for any $w\in L^{2}(\Omega, \mathbb {C}\otimes \mathbb {H})$![]() . Thus, we have
. Thus, we have
The estimates (5.2) follow from the estimate (3.8) (or the estimate (4.9) in the case of $\Omega$![]() unbounded). Indeed, we have
unbounded). Indeed, we have

for $s_1\in \mathbb {R}\setminus \{0\}$![]() and $j\in \mathbb {S}$
and $j\in \mathbb {S}$![]() . This estimate implies
. This estimate implies
so that we obtain
In conclusion, if we set
estimates (5.4) and (5.1) yield

and

for any $s = {\bf j} s_1\in \mathbb {H}\setminus \{0\}$![]() .
.
Thanks to the above results, we are now ready to establish our main statement.
Theorem 5.2 Under the hypotheses of Theorem 3.2 or of Theorem 4.3, for any $\alpha \in (0,1)$![]() and $v\in \mathcal {D}(T)$
and $v\in \mathcal {D}(T)$![]() , the integral
, the integral
converges absolutely in $L^{2}$![]() .
.
Proof. The right $S$![]() -resolvent equation implies
-resolvent equation implies
and so

As $\alpha \in (0,1)$![]() , the estimate (5.2) now yields
, the estimate (5.2) now yields

6. Concluding remarks
We list in the following some references associated with the spectral theory on the $S$![]() -spectrum and some research directions in order to orientate the interested reader in this field. Moreover, we give some references for classical fractional problems for scalar operators.
-spectrum and some research directions in order to orientate the interested reader in this field. Moreover, we give some references for classical fractional problems for scalar operators.
(I) In the literature, there are several nonlinear models that involve the fractional Laplacian and even the fractional powers of more general elliptic operators, see for example, the books [Reference Bucur and Valdinoci11, Reference Vazquez34].
(II) The $S$
 -spectrum approach to fractional diffusion problems used in this paper is a generalization of the method developed by Balakrishnan, see [Reference Balakrishnan5], to define the fractional powers of a real operator $A$
-spectrum approach to fractional diffusion problems used in this paper is a generalization of the method developed by Balakrishnan, see [Reference Balakrishnan5], to define the fractional powers of a real operator $A$ . In the paper [Reference Colombo and Gantner13], following the book of M. Haase, see [Reference Haase29], has developed the theory on fractional powers of quaternionic linear operators, see also [Reference Alpay, Colombo, Qian and Sabadini2, Reference Colombo and Gantner14].
. In the paper [Reference Colombo and Gantner13], following the book of M. Haase, see [Reference Haase29], has developed the theory on fractional powers of quaternionic linear operators, see also [Reference Alpay, Colombo, Qian and Sabadini2, Reference Colombo and Gantner14].(III) The spectral theorem on the $S$
 -spectrum is also an other tool to define the fractional powers of vector operators, see [Reference Alpay, Colombo and Kimsey1] and for perturbation results, see [Reference Cerejeiras, Colombo, Kähler and Sabadini12].
-spectrum is also an other tool to define the fractional powers of vector operators, see [Reference Alpay, Colombo and Kimsey1] and for perturbation results, see [Reference Cerejeiras, Colombo, Kähler and Sabadini12].(IV) An historical note on the discovery of the $S$
 -resolvent operators and of the $S$
-resolvent operators and of the $S$ -spectrum can be found in the introduction of the book [Reference Colombo, Gantner and Kimsey20].
-spectrum can be found in the introduction of the book [Reference Colombo, Gantner and Kimsey20].The most important results in quaternionic operators theory based on the $S$
 -spectrum and the associated theory of slice hyperholomorphic functions are contained in the books [Reference Alpay, Colombo and Sabadini3, Reference Alpay, Colombo and Sabadini4, Reference Colombo and Gantner16, Reference Colombo, Sabadini and Struppa18–Reference Colombo, Gantner and Kimsey20, Reference Gal and Sabadini27, Reference Gentili, Stoppato and Struppa28], for the case on $n$
-spectrum and the associated theory of slice hyperholomorphic functions are contained in the books [Reference Alpay, Colombo and Sabadini3, Reference Alpay, Colombo and Sabadini4, Reference Colombo and Gantner16, Reference Colombo, Sabadini and Struppa18–Reference Colombo, Gantner and Kimsey20, Reference Gal and Sabadini27, Reference Gentili, Stoppato and Struppa28], for the case on $n$ -tuples of operators see [Reference Colombo, Sabadini and Struppa17].
-tuples of operators see [Reference Colombo, Sabadini and Struppa17].(V) Our future research directions will consider the development of ideas from one and several complex variables, such as in [Reference Baracco, Pinton and Zampieri6–Reference Barletta, Dragomir and Peloso9, Reference Harrington, Peloso and Raich30–Reference Müller, Peloso and Ricci32] to the quaternionic setting.
Acknowledgements
The second author is partially supported by the PRIN project Direct and inverse problems for partial differential equations: theoretical aspects and applications.
Data availability
There is no data associate with this research.
Competing interests declaration
The authors declare none.