Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:47:34.711Z Has data issue: false hasContentIssue false
  • English
  • Français

The “Fourier” Theory of the Cardinal Function

Published online by Cambridge University Press:  20 January 2009

J. M. Whittaker
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The generalised Riesz-Fischer theorem states that if

is convergent, with 1 < p ≤ 2, then

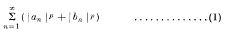
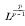is the Fourier series of a function of class . When p > 2 the series (2) is not necessarily a Fourier series; neither is it necessarily a Fourier D-series. It will be shown below that it must however be what may be called a “Fourier Stieltjes” series. That is to say, the condition (1) with (p > 1) implies that there is a continuous function F (x) such that

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 1 , Issue 3 , July 1928 , pp. 169 - 176
Copyright
Copyright © Edinburgh Mathematical Society 1928

References

page 169 note 1 Hobson, . Functions of a Real Variable (1926), vol. II., p. 599.Google Scholar

page 19 note 2 ibid., p. 488.

page 169 note 3 Cf. E. T. Whittaker, Proc. Roy. Soc. Edin., 35 (1915), 181. W. L. Ferrar, ibid., (1925), 269 ; 46 (1926). 323, and 47 (1927), 230. J. M. Whittaker, Proc. Edin. Math. Soc. (2), 1 (1927), 41. E. T. Copson, ibid., p. 129.

page 170 note 1 CfHobson, . loc. cit., vol. I., p. 506.Google Scholar

page 172 note 1 Monatshefte für Math. u. Physik, 32 (1922), 84.Google Scholar

page 172 note 2 Hobson, . loc. cit., vol. II., pp. 560, 580.Google Scholar

page 172 note 3 cf. sec. 3.Google Scholar

page 173 note 1 By a theorem due to Hyslop, Proc. Edin. Math. Soc., 44 (1926), 79.Google Scholar

page 174 note 1 This process is legitimate, cfHobson, , loc. cit., p. 582.Google Scholar

page 174 note 2 Proc. Land. Math. Soc., 2, 26 (1926), 12.Google ScholarProc. Camb. Phil. Soc., 23 (1926), 373.CrossRefGoogle ScholarSee also Miss Grimshaw, M. E., “A case of distinction between Fourier integrals and Fourier series”, loc. cit., p. 755.Google Scholar

page 174 note 3 Bull, de I'Acad. Roy. de Belg. (Clause de Sciences) (1908), pp. 319–410 esp. p. 341.Google Scholar

page 176 note 1 Proc. Lond. Math. Soc. (2), 26 (1926), 1.Google Scholar